
رگرسیون خطی با وزن محلی (رگرسیون وزنی محلی) در پایتون
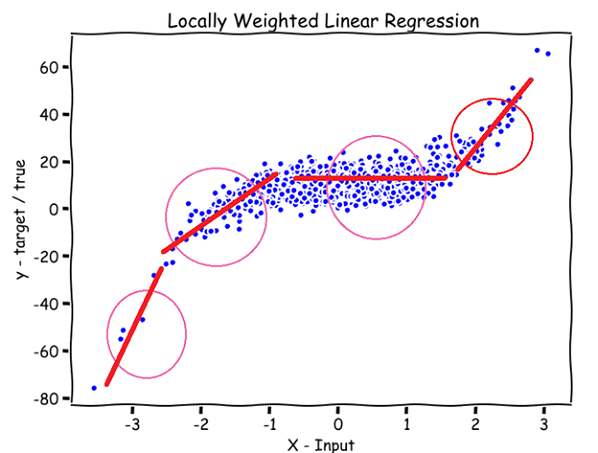
در این نوشتار، با پیادهسازی یک الگوریتم غیرپارامتری به نام رگرسیون خطی وزنی محلی آشنا میشویم. بدین منظور، ابتدا نگاهی به تفاوت بین الگوریتمهای یادگیری پارامتری و غیرپارامتری خواهیم انداخت. سپس تابع وزندهی و تابع پیشبینی را توضیح خواهیم داد. در انتها، پیشبینیهای تولیدشده را با استفاده از کتابخانههای NumPy و Matplotlib پایتون مصورسازی خواهیم کرد.
مطالب مجموعه «مقدمات یادگیری ماشینی»
- رگرسیون خطی در پایتون
- رگرسیون خطی با وزن محلی (وزنی محلی) در پایتون
- معادلات نرمال در پایتون، راهکاری فرمبسته برای رگرسیون خطی
- رگرسیون چندجملهای در پایتون
- رگرسیون لوجیستیک در پایتون
مقایسه الگوریتمهای یادگیری پارامتری و غیرپارامتری
پارامتری: در الگوریتمهای پارامتری، یک ثابت مجموعه پارامتر مشخص مثل theta داریم و هدف این است که طی آموزش داده ها، مقدار بهینه آن پارامترها را پیدا کنیم. بعد از پیدا کردن مقادیر بهینه این پارامترها، میتوانیم دادهها را کنار بگذاریم یا بهطور کل از کامپیوتر پاک کنیم؛ یعنی برای پیشبینی، میتوانیم تنها از پارامترهای مدل استفاده کنیم. بهخاطر داشته باشید که مدل صرفاً یک تابع است.
غیرپارامتری: در الگوریتمهای غیرپارامتری، همیشه باید دادهها و پارامترها را در حافظه کامپیوتر نگه داریم، تا بتوانیم پیشبینی انجام دهیم. به همین دلیل، اگر دیتاست خیلی بزرگ باشد، این الگوریتمها کاربردی نخواهند بود.
رگرسیون خطی وزنی محلی
اینجا میخواهیم از دادههایی که بهصورت تصادفی تولید شدهاند، بهعنوان مثال استفاده کنیم، تا رگرسیون خطی وزنی محلی را بهتر درک کنیم.
import numpy as npnp.random.seed(8)X = np.random.randn(1000,1)
y = 2*(X**3) + 10 + 4.6*np.random.randn(1000,1)
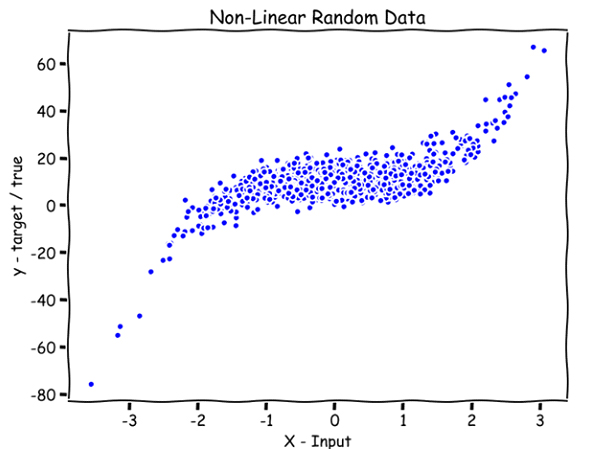
اگر بهخاطر داشته باشید، در رگرسیون خطی میتوانستیم یک خط صاف را روی دادهها برازش دهیم؛ اما اینجا دادهها غیرخطی هستند و اگر از یک خط صاف استفاده کنیم، پیشبینی بهشدت دچار خطا میشود. پس برای به حداقل رساندن این خطا، باید یک خط منحنی روی دادهها برازش دهیم.
نمادها
n: تعداد ویژگیها (که در این مثال ۱ است)
m: تعداد نمونههای آموزشی (که در این مثال ۱۰۰۰ است)
X (حرف بزرگ): ویژگیها
y: توالی خروجی
x (حرف کوچک): نقطهای که میخواهیم پیشبینی کنیم؛ در کدها بهصورت point مشخص میشود.
x(i): iمین نمونه آموزشی
در رگرسیون خطی وزنی محلی، x مربوط به قسمتی را که میخواهیم پیشبینی کنیم، به مدل میدهیم. مدل به همه x(i)های اطراف x وزن بیشتر (نزدیک به ۱) و به بقیه x(i)ها وزنی کمتر (نزدیک ۰) میدهد و سپس یک خط صاف را روی آن x(i)هایی که وزن بیشتری گرفتهاند، برازش میدهد.
بنابراین، وقتی بخواهیم نقطه سبز روی محور x (در تصویر پایین) را پیشبینی کنیم، مدل به دادههای ورودی x(i) که نزدیک یا اطراف دایره بالای نقطه سبزرنگ هستند، وزن بیشتری میدهد؛ بقیه x(i)ها وزنی نزدیک صفر دریافت میکنند. در نتیجه، مدل یک خط صاف را تنها روی دادههای نزدیک به دایره برازش میدهد. برای نقطه بنفش، زرد و خاکستری هم پیشبینی به همین ترتیب انجام میشود.
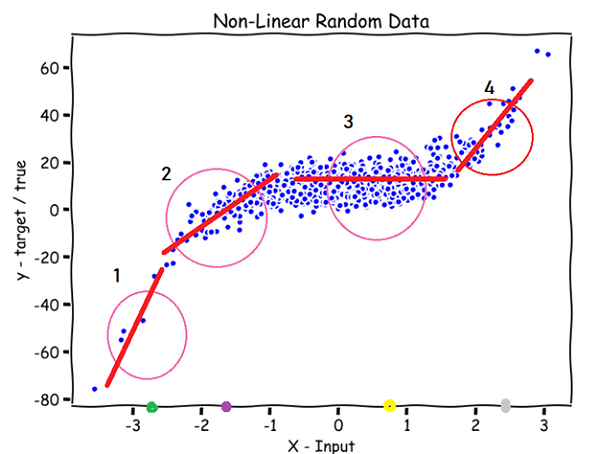
با توضیحاتی که در این قسمت ارائه شد، باید پاسخ دو سؤال را پیدا کنیم:
۱. وزنها چطور به متغیرها اختصاص داده میشوند؟
۲. اندازه دایره باید چقدر باشد؟
تابع وزندهی
w(i): وزن نمونه iم
در رگرسیون خطی، تابع زیان برابر بود با:
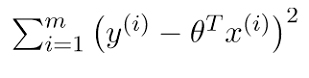
منبع: geeksforgeeks.org
در رگرسیون وزنی محلی، تابع زیان کمی تغییر مییابد:
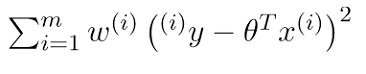
منبع: geeksforgeeks.org
تفاوت بین این دو معادله فقط مربوط به w(i) (یعنی وزن نمونه iم) است که بدین طریق محاسبه میشود:
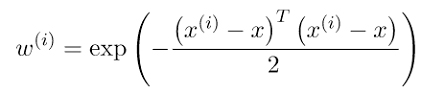
منبع: geeksforgeeks.org
در این معادله، x نقطهای است که میخواهیم پیشبینی کنیم؛ x(i) هم iمین نمونه آموزشی ماست.
مقدار این تابع همواره عددی بین ۰ تا ۱ خواهد بود.
با نگاه به این تابع در مییابیم:
- اگر |x(i)-x| کوچک باشد، w(i) نزدیک ۱ خواهد بود.
- اگر |x(i)-x| بزرگ باشد، w(i) نزدیک ۰ خواهد بود.
x(i)هایی که از x دور باشند، w(i) نزدیک به صفر دریافت خواهند کرد و بالعکس، x(i)هایی که نزدیک به x باشند، w(i) نزدیک ۱ میگیرند.
اگر بخواهیم همین توضیحات را از نظر تابع زیان بیان کنیم، میتوانیم بگوییم که x(i)های دور از x در مقداری نزدیک به ۰ و x(i)های نزدیک به x در مقداری نزدیک به ۱ ضرب میشوند. به بیان خلاصه، فقط مقادیری در خروجی تأثیر میگذارند که در مقداری نزدیک به ۱ ضرب شده باشند.
اندازه دایره باید چقدر باشد؟
در تابع وزندهی، هایپرپارامتر tau را تعریف میکنیم که اندازه دایره را تعیین میکند:
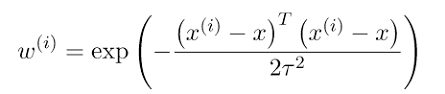
منبع: geeksforgeeks.org
با تغییر مقدار tau ، میتوانیم اندازه دایره را تغییر دهیم.
اگر پیشزمینهای در ریاضیات داشته باشید، احتمالاً میدانید که tau، پهنای منحنی زنگولهای (گاوسی) تابع وزندهی است.
در این قسمت کد مربوط به ماتریس وزندهی را مشاهده میکنید؛ به کامنتها توجه کنید.
# Weight Matrix in code. It is a diagonal matrix.def wm(point, X, tau):
# tau --> bandwidth
# X --> Training data.
# point --> the x where we want to make the prediction.
# m is the No of training examples .
m = X.shape[0]
# Initialising W as an identity matrix.
w = np.mat(np.eye(m))
# Calculating weights for all training examples [x(i)'s].
for i in range(m):
xi = X[i]
d = (-2 * tau * tau)
w[i, i] = np.exp(np.dot((xi-point), (xi-point).T)/d)
return w
الگوریتم
این الگوریتم یک حل فرمبسته نیز دارد؛ یعنی میتوان بدون نیاز به آموزش مدل و با استفاده از فرمول پایین، پارامتر theta را مستقیماً محاسبه کرد:
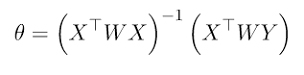
منبع: geeksforgeeks.org
محاسبه theta
تنها کافیست مشتق تابع زیان نسبت به theta را گرفته و آن را برابر با ۰ قرار دهیم. سپس با اجرای مقداری عملیات جبر خطی، مقدار theta را به دست میآوریم.
برای توضیحات بیشتر میتوانید به این لینک رجوع کنید.
بعد از محاسبه theta ، از طریق فرمول پایین پیشبینی را انجام میدهیم:
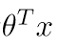
منبع: geeksforgeeks.org
در این قسمت کد مربوط به تابع پیشبینی را مشاهده میکنید؛ به کامنتها توجه داشته باشید:
def predict(X, y, point, tau):
# m = number of training examples.
m = X.shape[0]
# Appending a cloumn of ones in X to add the bias term.
## # Just one parameter: theta, that's why adding a column of ones #### to X and also adding a 1 for the point where we want to #### predict.
X_ = np.append(X, np.ones(m).reshape(m,1), axis=1)
# point is the x where we want to make the prediction.
point_ = np.array([point, 1])
# Calculating the weight matrix using the wm function we wrote # # earlier.
w = wm(point_, X_, tau)
# Calculating parameter theta using the formula.
theta = np.linalg.pinv(X_.T*(w * X_))*(X_.T*(w * y))
# Calculating predictions.
pred = np.dot(point_, theta)
# Returning the theta and predictions
return theta, pred
مصورسازی پیشبینیها
در این قسمت میخواهیم پیشبینیهایی را که از ۱۰۰ نقطه x انجام دادهایم، مصورسازی کنیم؛ به کامنتها توجه داشته باشید.
def plot_predictions(X, y, tau, nval): # X --> Training data.
# y --> Output sequence.
# nval --> number of values/points for which we are going to
# predict. # tau --> the bandwidth.
# The values for which we are going to predict.
# X_test includes nval evenly spaced values in the domain of X.
X_test = np.linspace(-3, 3, nval)
# Empty list for storing predictions.
preds = []
# Predicting for all nval values and storing them in preds.
for point in X_test:
theta, pred = predict(X, y, point, tau)
preds.append(pred)
# Reshaping X_test and preds
X_test = np.array(X_test).reshape(nval,1)
preds = np.array(preds).reshape(nval,1)
# Plotting
plt.plot(X, y, 'b.')
plt.plot(X_test, preds, 'r.') # Predictions in red color.
plt.show()plot_predictions(X, y, 0.08, 100)
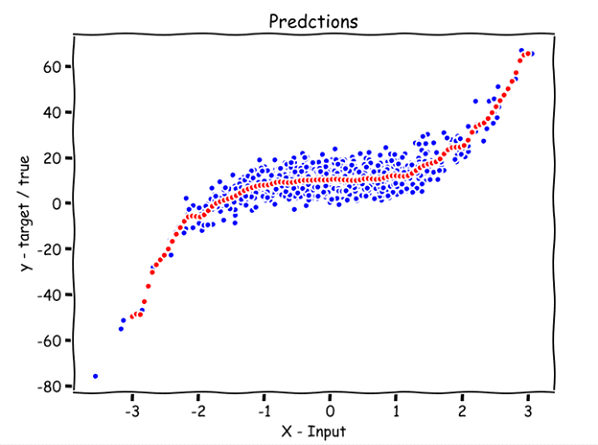
نقاط قرمز پیشبینی ۱۰۰ عدد با فواصل منظم بین ۳- تا ۳ هستند
چه زمانی از رگرسیون خطی وزنی محلی استفاده میشود؟
- وقتی n (تعداد ویژگیها) کوچک باشد.
- در صورتی که نمیخواهید یا نمیتوانید ویژگیهای لازم را انتخاب کنید.






















