با الگوریتم‌های بهینه‌سازی مختلف برای آموزش شبکه عصبی آشنا شویم

ممکن است بسیاری از افراد بدون اطلاع از روش بهینه‌سازی، از بهینه‌سازها هنگام آموزش شبکه عصبی استفاده کنند. بهینه‌سازها به الگوریتم‌ها یا روش‌هایی اطلاق می‌شود که برای تغییر ویژگی‌های شبکه عصبی از قبیل وزن و نرخ یادگیری کار برده می‌شوند. این کار، نقش موثری در کاهش زیان losses دارد. نحوه تغییر وزن‌ها یا نرخ یادگیری شبکه عصبی به ابزارهای بهینه‌سازیِ مورد استفاده بستگی دارد. راهبردها یا الگوریتم‌های بهینه‌سازی مسئول کاهش زیان هستند و دقیق‌ترین نتایج ممکن را به ارمغان می‌آورند. در مقاله حاضر، انواع مختلف بهینه‌سازها و مزایای آنهابرای آموزش شبکه عصبی توضیح داده خواهد شد.

گرادیان کاهشی

گرادیان کاهشی Gradient Descent اساسی‌ترین و پرکاربردترین الگوریتم بهینه‌سازی به حساب می‌آید که به طور گسترده در رگرسیون خطی و الگوریتم‌های طبقه‌بندی استفاده می‌شود. روش پس‌انتشار Backpropagation در شبکه‌های عصبی نیز از الگوریتم گرادیان کاهشی استفاده می‌کند. گرادیان کاهشی به الگوریتم بهینه‌سازی مرتبه اول گفته می‌شود که به مشتق مرتبه اولِ first order derivative تابع زیان بستگی دارد. محاسبات این الگوریتم تعیین می‌کند که وزن‌ها چگونه باید تغییر یابند تا تابع به مقدار کمینه برسد. با روش پس‌انتشار، زیان از یک لایه به لایه دیگر انتقال یافته و پارامترهای مدل (موسوم به وزن) نیز بسته به زیان تغییر می‌یابند تا زیان به حداقل برسد.

مزایا:

1. محاسبه آسان
2. اجرای آسان
3. درک آسان

معایب:

1. احتمالِ گیر افتادن در دام کمینه محلی local minima.
2. وزن‌ها پس از محاسبه گرادیان در کل مجموعه‌داده تغییر می‌یابند. بنابراین، اگر مجموعه‌داده بسیار بزرگتر از این باشد، ممکن است سال‌ها طول بکشد تا مقدار کمینه بدست آید.
3. نیاز به حافظه بزرگ برای محاسبه گرادیان در کل مجموعه‌داده.

گرادیان کاهشی تصادفی

گرادیان کاهشی تصادفی Stochastic Gradient Descent یکی از گونه‌های گرادیان کاهشی است. این گرادیان، پارامترهای مدل را به طور پیوسته به‌روزرسانی می‌کند. در این روش، پارامترهای مدل پس از محاسبه زیان در هر نمونه آموزش تغییر می‌یابند. بنابراین، اگر مجموعه‌داده 1000 ردیف داشته باشد، گرادیان کاهشی تصادفی پارامترهای مدل را 1000 بار در یک چرخه از مجموعه‌داده به‌روزرسانی می‌کند؛ برخلاف گرادیان کاهشی که عمل به‌روزرسانی فقط یک بار در آن انجام می‌شد.

بر این اساس، {x(i) ,y(i)} نمونه‌های آموزشی هستند.

از آنجایی که پارامترهای مدل به طور مرتب به‌روزرسانی می‌شوند، پارامترها واریانس و نوسان بالایی در توابع زیان دارد؛ شدت آن فرق می‌کند.

مزایا:

1. به‌روزرسانی پیوسته‌ی پارامترهای مدل؛ نتیجه: همگرایی در زمان کمتر
2. نیاز به حافظه کمتر زیرا ذخیره‌سازیِ مقادیر توابع زیان الزامی نیست.
3. احتمال بدست آوردن کمینه‌ی جدید

معایب:

1. واریانس بالا در پارمترهای مدل
2. احتمال ادامه فعالیت حتی پس از بدست آوردن کمینه کلی.
3. برای اینکه همگراییِ شبیه به گرادیان کاهشی به دست آید، مقدار نرخ یادگیری به آرامی کاهش می‌یابد.

گرادیان کاهشی Mini-Batch

بهترین نوع گرادیان در میان کلیه الگوریتم‌های گرادیان کاهشی است. این الگوریتم نسخه‌ پیشرفته‌یِ گرادیان کاهشی تصادفی و گرادیان کاهشی استاندارد است. این گرادیان پس از هر دسته اقدام به به‌روزرسانی پارامترهای مدل می‌کند. بنابراین، مجموعه‌داده به دسته‌های (batch) مختلفی تقسیم می‌شود. پارامترها پس از هر دسته به‌روزرسانی می‌شوند.

بر این اساس، {B(i)} به عنوان دسته یا batch شناخته می‌شوند.

مزایا:

1. پارامترهای مدل را به طور مرتب به‌روزرسانی می‌کند و واریانس کمتری دارد.
2. به حافظه متوسط نیاز دارد.

همه الگوریتم‌ها گرادیان کاهشی با چالش‌هایی روبرو هستند:

1. انتخاب مقدار بهینه‌ی نرخ یادگیری. اگر نرخ یادگیری خیلی کوچک باشد، ممکن است همگرایی مدت زمان بسیاری به طول انجامد.
2. داشتن نرخ یادگیری ثابت برای همه پارامترها. ممکن است پارامترهایی وجود داشته باشیم که شاید تمایلی به تغییرشان با نرخ یکسان نداشته باشیم.
3. احتمالِ گیر افتادن در دام کمینه محلی

تکانه(مومنتوم)

تکانه Momentum با هدفِ کاهش واریانس در گرادیان کاهشی تصادفی ابداع شد. تکانه، همگرایی به جهت مورد نظر را تسریع بخشیده و از گرایش به جهات نامربوط پیشگیری می‌کند. در این روش به جای اینکه تنها از مقدار گرادیان در مرحله ی فعلی به منظور هدایت جستجو استفاده شود، تکانه گرادیان مراحل گذشته را نیز محاسبه می کند و از آن برای تعیین جهت گرادیان استفاده می کند. هایپرپارامتر دیگری موسوم به تکانه در این روش استفاده می‌شود.

اکنون، وزن‌ها با  به‌روزرسانی می‌شوند.

عبارت تکانه  معمولاً 9/0 یا مقداری مشابه در نظر گرفته می‌شود.

مزایا:

1. کاهشِ نوسانات و واریانس بالای پارامترها
2. همگرایی سریع در مقایسه با گرادیان کاهشی.

معایب:

1. هایپرپارامتر دیگری افزوده می‌شود. باید آن را به صورت دستی و دقیق انتخاب کرد.

گرادیان شتاب‌یافته‌ی نستروف

شاید تکانه روش خوبی باشد، اما اگر تکانه خیلی زیاد باشد، ممکن است الگوریتم کمینه محلی را از دست دهد و حتی به افزایش خود ادامه دهد. بنابراین، محاسبه‌ی θ−γυ_t-1  تقریبی از مقدار بعدی بردار پارامترها را به دست می‌دهد (گرادیان که در میزان تغییرات موثر است در اینجا در نظر گرفته نشده)؛ با این کار درکی مناسب از مقادیر بعدی پارامترها به دست می‌آوریم. اکنون می‌توانیم با محاسبه گرادیان نسبت به مقدار تقریبی بعدی پارامترها، نه مقدار فعلی آن‌ها، به طور موثری مقدار بعدی داده‌ها را در محاسبات دخیل کنیم:

امکان به‌روزرسانی پارامترها با استفاده از  نیز وجود دارد.

مزایا:

1. کمینه محلی را از دست نمی‌دهد.
2. اگر کمینه‌ای در کار باشد، آهسته‌تر عمل می‌کند.

معایب:

1. هایپرپارامتر کماکان باید به صورت دستی انتخاب شود.

روش گرادیان انطباقی (AdaGrad)

یکی از معایب همه بهینه‌سازهایی که تا بدین‌جا توضیح داده شد، این است که نرخ یادگیری در همه پارامترها و چرخه‌ها ثابت است. روش فعلی، نرخ یادگیری  را برای هر پارامتر و هر بازه زمانی  تغییر می‌دهد و یک الگوریتم بهینه‌سازی مرتبه دوم به شمار می‌آید که با مشتق تابع خطا کار می‌کند.

مشتق تابع زیانِ پارامترهای مشخص در زمانی مشخص t

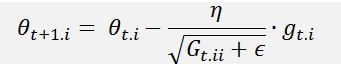
به‌روزرسانی پارامترها با ورودی مشخص i و زمان/تکرار t

در اینجا، η نرخ یادگیری است که بر اساس گرادیان‌های پیشین، در پارامتر θ(i) و زمانی مشخص تغییر می‌یابد. هر درایه‌ی قطری i,i جمع مربعات گرادیان‌ها نسبت به θi در گام زمانی t است و ϵ یک ضریب هموارسازی است که از ایجاد صفر در مخرج جلوگیری می‌کند (معمولا در مقیاس 10-8 است). جالب است که بدون جذر گرفتن، الگوریتم عملکرد بسیار ضعیف‌تری دارد.

مزایا:

1. تغییر نرخ یادگیری در هر پارامتر آموزش
2. عدم نیاز به تنظیم دستیِ نرخ یادگیری
3. امکان آموزش با داده‌های پراکنده

معایب:

1. نیاز به محاسبات سنگین در هنگام محاسبه مشتق مرتبه دوم
2. کاهش نرخ یادگیری در پی آموزش کُند

AdaDelta

روش AdaDelta بسطی از روش AdaGrad است که هدف آن کمتر کردن کاهش فزاینده و یکنواخت نزخ یادگیری در این روش است. به جای تجمع مربعات همه‌ی گرادیان‌های قبلی، روش AdaDelta تعداد مربعات جمع شده را به تعداد محدودی مثل w محدود می‌کند. به جای ذخیره‌ی غیربهینه‌ی wتا از مربعات گرادیان‌ها، جمع گرادیان به صورت بازگشتی، میانگین میراشونده‌ی همه‌ی مربعات گرادیان‌های قبلی تعریف می‌شود. میانگین در لحظه‌ی t یعنی E[g2]t فقط (با یک کسر γ که شبیه به ثابت شتاب است) به میانگین قبلی و گرادیان فعلی بستگی دارد:

به γ مقداری شبیه به ثابت سرعت یعنی حدود 9/0 می‌دهیم.

مزایا:

1. حال، نرخ یادگیری کاهش نمی‌یابد و آموزش متوقف نمی‌شود.

معایب:

1. نیازمند محاسبات زیاد

روش Adam

روش تخمین تکانه تطبیق‌پذیر (Adam) با تکانه‌های مرتبه اول و دوم کار می‌کند. علاوه بر ذخیره کردن میانگین میراشونده‌ی نمایی مربعات گرادیان‌های قبلی، یعنی vt مثل روش‌های AdaDelta و RMSprop، روش Adam میانگین میراشونده‌ی نمایی گرادیان ها mt را هم مثل روش شتاب حفظ می‌کند. mt و vt به ترتیب تخمین تکانه اول (میانگین) و تکانه دوم (واریانس غیرمرکزی) گرادیان‌ها هستند که نام‌گذاری روش هم به همین خاطر است. به خاطر این که حالت اولیه ی بردارهای mt و vt صفر است، سازندگان روش مشاهده کردند که نتایج به صفر متمایل می‌شوند، به خصوص در گام‌های اولیه و مخصوصاً وقتی نرخ میراشوندگی کوچک است (یا به عبارت دیگر β1 و β2 نزدیک 1 هستند).

به‌روزرسانی پارامترها:

مقادیر پیشفرض 9/0 برای β1، 999/0 برای β2 و  ^8-10 برای ϵ پیشنهاد شده است.

مزایا:

1. این روش بسیار سریع است و به سرعت همگرایی پیدا می‌کند.
2. نرخ یادگیری و واریانس بالا را اصلاح می‌کند.

معایب:

1. هزینه‌های محاسباتی بالا

جمع‌بندی

در این مقاله انواع مختلف بهینه‌سازها و مزایای آنها برای آموزش شبکه عصبی توضیح داده شد. Adam بهترین الگوریتم بهینه‌سازی است. با Adam می‌توانید آموزش شبکه عصبی را در زمان کمتر و کارایی بالاتر انجام دهید.