
بررسی یادگیری ماشین کوانتومی با استفاده از «TensorFlow Quantum»
مقالۀ حاضر بر آن است تا یادگیری ماشین کوانتومی را برای مبتدیان توضیح دهد. این فناوری، آیندهی ناگزیری برای ایدههای یادگیری ماشینی رقم خواهد زد. در این مقاله، حوزههایی معرفی میشود که ادغام یادگیری ماشینی و محاسبه کوانتومی در آنها میتواند نقش مفیدی در حل مسائل داشته باشد. لذا مقاله به گونه ساماندهی شده است که در ابتدا به توصیف مفهوم محاسبه کوانتومی در رابطه با مسئله پرداخته شده و سپس از راهحلِ ارائه شده از سوی تیم کوانتوم هوش مصنوعی گوگل رونمایی میشود. افزون براین، تحقیقات پیشینِ کارشناسان کوانتوم هوش مصنوعی گوگل با همکاریِ دانشگاه واترلو، Alphabet’s X، و فولکسواگن پیرامون یادگیری ماشین کوانتومی با استفاده از «Tensorflow Quantum» بررسی میشود.
پیش از اینکه کارِ بررسی برخی از مسائل را آغاز کنیم، در ابتدا لازم میدانیم «Tensorflow Quantum» را معرفی کنیم. این کتابخانه منبع باز برای انجام محاسبات در دادههای کوانتومی و ساخت مدلهای یادگیری ترکیبیِ کوانتومی-کلاسیک مورد استفاده قرار میگیرد. مقالههای متعددی درباره جزئیات فنی این کتابخانه منتشر شده است که میتوانید به راحتی به آنها دسترسی پیدا کنید.
برای انجام محاسبات کوانتومی نیاز به مدارهای کوانتومی داریم که آنها یک محاسبه بوسیله توالی از گیتهای کوانتومی quantum gates انجام میشود. «Tensorflow Quantum» از «Cirq» برای طراحی منطق این مدارهای کوانتومی استفاده میکند. پیش از اینکه بحث را ادامه دهیم، توصیه میکنیم اطلاعاتی درباره رابط برنامهنویسی کاربردی «AIP» در «Tensorflow Quantum» و Cirq بدست بیاورید.
دستهبندی دوتاییِ دادههای کوانتومی
برای انجام این کار باید یک شبکه عصبی ترکیبی (کوانتومی-کلاسیک) طراحی کنیم تا امکانِ دستهبندی در میان منابع داده کوانتومی فراهم شود. دادههای کوانتومی از «Bloch sphere» به دست میآیند. در Bloch sphere، در ابتدا دو پرتو در صفحه XZ انتخاب کرده و سپس نقاطی را که به صورت تصادفی پیرامون پرتوها توزیع شدهاند، انتخاب میکنیم. پس کار اصلی این است که دو حباب حاصل از انتخاب پرتوهای فوق را جداسازی کنیم. عکسهای مربوط به دو زاویه مختلف در زیر نشان داده شده است: θ و ϕ. هر دوی این زوایا در صفحه XZ قرار دارند و با توجه به قسمت مثبت محور X اندازهگیری میشوند. در عکسهای زیر، θ زاویۀ ایجاد شده با پرتو آبی با محور X مثبت در صفحه XZ و ϕ به منزلۀ پرتو نارنجی است.
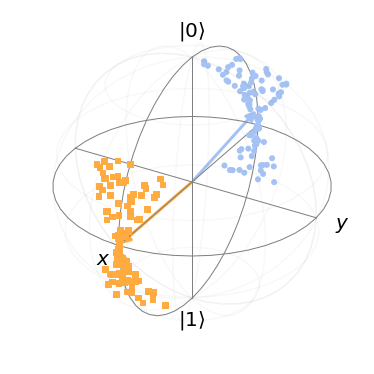

پس به این نتیجه میرسیم که امکان ساخت هر گونه حالت کوانتومی با استفاده از چرخش X و چرخش Z در «Bloch sphere» وجود دارد. یک مدل شبکه عصبیِ ترکیبی (کوانتومی-کلاسیک) برای کارِ دستهبندی فوق طراحی شده است. نمای کلیِ این شبکه در عکس زیر نشان داده شده است.

دادههای کوانتومی که در این مورد ایجاد میشوند، در واقع نقاطی در سطح فضای Bloch هستند. سپس یک مدار کوانتومی با استفاده از گِیتهای کوانتومی Cirq تحت عنوان Û با پارامترهای Φ ایجاد میشود. بعد از آن یک لایه نیز از کتابخانه «Tensorflow Quantum» انتخاب میشود تا محاسبات را در قالب کیوبیتها qubits در مدل کوانتومی انجام دهد. به مجرد اینکه محاسبه کوانتومی به پایان رسید، امید ریاضی expectation لایه خروجی بوسیله نمونهبرداری یا اندازهگیری میانگین مقادیر بدست آمده از کیوبیتها محاسبه میشوند. این کارِ اندازهگیری باعث حذف ماهیت کوانتومی کیوبیتها شده و به یک متغیر کلاسیک ختم میشود. این متغیر کلاسیک در اختیار یک مدل شبکه عصبی کلاسیک قرار داده میشود تا در نهایت از احتمالات پیشبینی خروجی گرفته شود. در عکس زیر، نمودار زیانِ شبکه عصبی ترکیبی نشان داده شده است. این شبکه برای دستهبندی نقاط پیرامون دو پرتو در سطح فضای Bloch آموزش داده میشود.کاهش خطای دستهبندی در طول آموزش و زیان نهایی 0.00085 در پایان آموزش نشان میدهد که شبکه عصبی ترکیبیِ پیشنهادی عملکرد موفقی در دستهبندیِ دادههای کوانتومی داشته است.
[irp posts=”15939″]
شبکههای عصبی بازگشتی گراف کوانتومی (QGRNN)
در این بخش میخواهیم دینامیک هدفHamiltonian را با استفاده از شبکه عصبی QGRNN در مدل Ising توضیح دهیم. مدل Ising در اینجا همان نسخۀ مدل کلاسیک Ising است که در ترمودینامیک و مغناطیس به کار برده میشود. هدفHamiltonian مدل Ising به صورت زیر است:

مدل Ising در محاسبات کوانتومی یک ساختار مشبک با اسپین کیوبیت است که در شکل فوق با حرف Z نشان داده شده است. J یک ضریب کوپلینگ است که قدرت برهمکنشهای میان جفت اسپینهای کیوبیت را نشان میدهد، در حالیکه B ضریب بایاس یا انحراف برای کیوبیت است. عبارتِ X با این هدف اضافه شده که تاثیر نسبی فیلدهای بیرونی را در کیوبیت نشان دهد. برهمکنش میان اسپینها میتواند نقش مفیدی در شبیهسازیِ چندین مدل یادگیری ماشینی داشته باشد. از جمله این مدلها میتوان به شبکههای هاپفیلد Hopfield networks و ماشینهای بولتزمن Boltzmann machines اشاره کرد (شولد و پتروسیون، سال 2018). علاوه بر این، مدل Ising از اصول ریاضیِ مسائل موسوم به «بهینهسازیِ دوتایی بیقید درجه دوم (QUBO)» تقلید میکند. با معرفی مدل Ising و Hamiltonian، مراحلی را در بخش زیر توضیح خواهیم داد که برای درک قابلیتهای دینامیک مدل Ising ضروری هستند.
آمادهسازیِ دادههای کوانتومی با ابزار حل کوانتومی Eigensolver در مدل Ising

حالا نوبت به ساخت ابزار حل کوانتومی (VQE) رسیده تا حالت انرژی پایینی نزدیک به حالت پایه پیدا کنیم؛ بدین ترتیب، میتوان از آن به عنوان حالت اولیۀ مدل Ising و QGRNN استفاده کرد. روش VQE راهکاری برای یافتن حالتهای انرژی پایه پیدا میکند. در بخش زیر، حالات انرژی پایینی که با آموزش VQE بدست آمده، نشان داده شده است.

ساخت مدل Ising و QGRNN
باید مقادیر نمایی Hamiltonians را برای ساخت مدل Ising محاسبه کنیم. با این حال، مقادیر نماییِ دو مورد قابلمشاهده با مقادیر نماییِ مجموع آنها برابر نیست. Suzuki-Trotter expansion برای حل این مسئله انتخاب شده است زیرا راهحلهای تقریبی ارائه میکند و نقش مهمی در آسان کردنِ مراحل محاسبه دارد. اکنون باید مدل QGRNN را راهاندازی کنیم. چون Hamiltonian در مدل QGRNN معلوم نیست، از یک نمودار تصادفی در QGRNN استفاده کردیم.
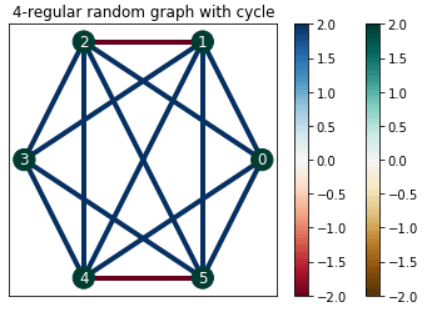
آموزش و نتایج حاصل از QGRNN


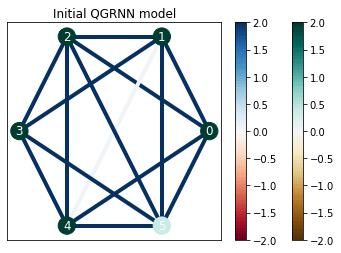

با توجه به تصاویر فوق میتوان دریافت که QGRNN ویژگیهای دینامیکی تکامل زمانی را از روی دادههای کوانتومی یاد میگیرد.
[irp posts=”10184″]ابزار Thermalizer کوانتومی VQT
در این بخش از TensorFlow Quantum برای بررسی ترکیب محاسبه کوانتومی و مدلهای کلاسیکِ انرژیمحور استفاده میشود. در اینجا، مدل دوبعدی هازینبرگ را بررسی کرده و از ابزار VQT برای ایجاد حالات گرمایی (Thermal) در مدل استفاده میشود. میتوانید در مقالههای مختلف به جزئیات VQT دسترسی پیدا کرده و آنها را مطالعه کنید.

مدلهای یادگیریِ مبتنی بر انرژی (EBM)
بر اساس مفهوم فیزیک و گروههای نمایی، از ماشین بولتزمن برای یادگیری دینامیکِ مدل دوبعدی هازینبرگ استفاده خواهد شد. مدل کلاسیک ماشین بولتزمن میتواند در صورت تعویض با عملگر پائولی Z به سرعت به مدل مکانیک کوانتومی Ising تبدیل شود. به محض اینکه ansatz با در نظر گرفتن همبستگی صفر میان کیوبیتها ایجاد شد، ماشین بولتزمن به چند توزیع بِرنولی مستقل در چند مجموعه کیوبیت تقلیل داده میشود. بنابراین، باید در وهله اول به اجرای Bernoulli EBM در VQT بپردازیم. در همین راستا میتوان از تابع زیان VQT استفاده کرد.
نتایج VQT با تبدیل Bernoulli EBM به مدل Ising
















از نتایجِ بدست آمده این چنین استنباط میشود که روشهای مبتنی بر انرژی در یادگیری دینامیک Hamiltonian در مدل دوبعدی هازینبرگ عملکرد موفقی داشتند. هدف ما در مقاله حاضر این بود که یادگیری ماشین کوانتومی را برای مبتدیان معرفی کرده وکاربرد محاسبه کوانتومی را در مسائل مختلف بررسی کنیم. توجه داشته باشید که باید همواره دانشتان را در خصوص یادگیری ماشین کوانتومی بهروز نگه دارید و مطالعه مقالههای مختلف در این زمینه به اولویتتان تبدیل شود.






