تأثیر اندازه بسته شبکه بر آموزش شبکه عصبی

تیم تحریریه
۹ آبان ۱۴۰۰

زمان مطالعه: 11 دقیقه

در این مقاله می‌خواهیم تأثیر اندازه بسته شبکه را بر آموزش شبکه‌های عصبی بیشتر بشناسیم. فهرست مطالب بدین صورت است:

اندازه بسته شبکه چیست؟
دلیل اهمیت اندازه بسته شبکه چیست؟
بسته‌های کوچک و بزرگ از نظر تجربی چگونه عمل می‌کنند؟
چرا بسته‌های بزرگتر عملکرد ضعیف‌تری دارند و چطور می‌توانیم آن را جبران کنیم؟

فهرست مقاله پنهان

1 اندازه بسته شبکه چیست؟

2 دلیل اهمیت اندازه بسته شبکه چیست؟

3 آزمایش‌ها چطور طراحی می‌شوند؟

4 اندازه بسته شبکه چه تأثیری بر آموزش دارد؟

5 چرا عملکرد بسته‌های کوچکتر بهتر است؟

6 آیا می‌توانیم با افزایش نرخ یادگیری عملکرد بسته‌های بزرگ را بهبود ببخشیم؟

7 آیا آموزش بسته‌های کوچک همیشه بهتر از آموزش بسته‌های بزرگ عمل می‌کند؟

اندازه بسته شبکه چیست؟

شبکه‌های عصبی به نحوی آموزش دیده‌اند که توابع زیان به شکل زیر را کمینه کنند:

شکل 1 تابع زیان منبع (1): Keskar et al.

در فرمول بالا:

پارامترهای مدل را نشان می‌دهد.
m تعداد نمونه داده‌های آموزشی است.
هر مقدار i معرف یک نمونه داده آموزشی واحد است.
نشان‌دهنده تابع زیانی است که برای یک نمونه آموزشیِ واحد اجرا شده است.

به حداقل رساندن تابع زیان معمولاً با کاهش گرادیان Gradient descent، یعنی محاسبه گردایان تابع زیان با توجه به پارامترها، انجام می‌شود. کاهش تدریجی گرادیان، گرادیان یک زیرمجموعه از داده‌های آموزشی ( $B_{k}$ ) را به جای همه داده‌های دیتاست محاسبه می‌کند.

شکل 2 معادله‌ جدید کاهش تدریجی گرادیان منبع (1)

$B_{k}$ بسته‌ای است که به‌عنوان نمونه از داده‌های دیتاست آموزشی گرفته شده و اندازه آن از 1 تا m (شمار کلی نقاط داده‌ای آموزشی) متغیر است (1). به این مرحله اصطلاحاً «آموزش خرده‌بسته Mini-batch» با اندازه $B_{k}$ گفته می‌شود. می‌توان این گرادیان‌های در سطح بسته‌ای Batch-level gradients را برآورد گرادیان «واقعی» در نظر گرفت (گرادیان واقعی یعنی گرادیان کل تابع زیان با توجه به θ). به این خاطر از خرده‌بسته‌ها استفاده می‌کنیم که تمایل به همگرایی در آن‌ها زیاد است، زیرا نیازی به اینکه برای به‌روزرسانی وزن‌های خود به‌طور کامل از داده‌های آموزشی بگذرند، ندارند.

[irp posts=”5325″]

دلیل اهمیت اندازه بسته شبکه چیست؟

کسکارKeskar و همکارانش در کار خود متوجه شدند که فرآیند گرادیان کاهشی تصادفی متوالی بوده و از خرده‌بسته‌ها استفاده می‌کند، بنابراین نمی‌توان به‌راحتی آن‌ها را موازی‌سازی کرد (1). استفاده از بسته‌هایی با اندازه‌های بزرگتر تا حد زیادی به ما امکان موازی‌سازی محاسبات را می‌دهد، زیرا می‌توانیم نمونه‌های آموزشی را بین گره‌های مختلف کارگر Worker nodes تقسیم کنیم. در نتیجه این قابلیت می‌توان به آموزش مدل سرعت بخشید.

در حالیکه میزان خطای آموزشی در بسته‌های بزرگتر به اندازه بسته‌های کوچکتر است، این بسته‌ها قابلیت تعمیمپذیری ضعیف‌تری به داده‌های آزمون دارند (1). به فاصله بین خطای آموزش و خطای آزمون، «فاصله تعمیم‌پذیری Generalization gap» گفته می‌شود.

بنابراین می‌توان گفت ایده‌آل این است که خطای آزمون در حد خطای بسته‌های کوچکتر باشد. در این صورت می‌توانیم سرعت آموزش را بدون از دست دادن دقت مدل به طرز معناداری افزایش دهیم.

آزمایش‌ها چطور طراحی می‌شوند؟

همان‌طور که در اولین مقاله در مورد بهینه‌سازها توضیح داده شد، یکی از شبکه های عصبی را با استفاده از بسته‌هایی با اندازه‌های گوناگون آموزش می‌دهیم و سپس عملکرد آن‌ها را با هم مقایسه می‌کنیم.

دیتاست: از دیتاست‌های گربه و سگ که شامل 23262 تصویر از گربه و سگ است استفاده می‌کنیم و این تصاویر را به صورت نصف نصف در دو دسته تقسیم می‌کنیم. از آنجایی که اندازه تصاویر با هم متفاوت است، همه آن‌ها را هم‌اندازه می‌کنیم. از 20% داده‌های دیتاست به‌عنوان داده‌های اعتباریابی Validation data (dev set) و از بقیه به‌عنوان داده‌های آموزشی استفاده می‌کنیم.
معیار ارزیابیEvaluation metric: معیار اصلی ما، تابع زیان آنتروپی متقاطع دوسویهBinary cross-entropy است که به‌منظور اعتباریابی داده‌ها استفاده می‌شود.

شکل 3 نمونه‌هایی از تصاویر گربه‌ها و سگ‌ها در داده‌ها

مدل پایهBase model : یک مدل پایه تعریف می‌کنیم که وام گرفته از معماری VGG16 است و در آن، با استفاده از تابع فعال‌سازی ReLU عملیات‌ها را مکرراً انجام می‌دهیم (convolution ->max-pool). سپس حجم خروجی را صاف کرده و آن را وارد دو لایه کاملاً متصل و درنهایت وارد یک لایه تک-نورونی One-neuron layer با فعال‌سازی سیگموئید Sigmoid activation می‌کنیم که خروجی‌هایی بین 0 تا 1 به دست می‌دهد. این خروجی‌ها به ما می‌گویند که مدل گربه (0) پیش‌بینی می‌کند یا سگ (1).

آموزش: از گرادیان کاهشی تصادفی (SGD) با نرخ یادگیری 0/01 استفاده می‌کنیم. سپس مدل را تا 100 مرحله و تا زمانی که تابع زیان اعتباریابی Validation loss دیگر قادر به تولید مقادیر بهتری نباشد، آموزش می‌دهیم.

اندازه بسته شبکه چه تأثیری بر آموزش دارد؟

بیایید با استفاده از داده‌های دیتاست سگ و گربه که پیشتر توضیح داده شد، اندازه‌بسته‌های گوناگون را امتحان کنیم و عملکرد آن‌ها را مشاهده کنیم.

شکل 5 منحنی‌های زیان اعتباریابی و آموزش برای اندازه بسته‌های گوناگون

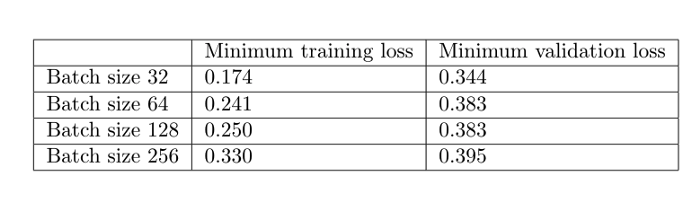
شکل 6 بهترین توابع زیان به دست آمده برای هر اندازه بسته

شکل 7 چپ: میانگین زمان بر حسب دوره وسط: تعداد دوره تا زمان همگرایی تابع زیان اعتباریابی راست: زمان کلی آموزش تا زمان همگرایی تابع زیان اعتباریابی

از توابع بالا می‌توان نتیجه گرفت که هرچه اندازه بسته شبکه بزرگتر باشد:

سرعت کاهش تابع زیان آموزش Training loss کمتر خواهد بود.
تابع زیان اعتباریابی بالاتر خواهد بود.
برای آموزش هر دورهepoch زمان کمتری نیاز است.
تعداد دوره‌های بیشتری برای ایجاد تابع زیان حداقلی اعتبار لازم است.

اکنون به هرکدام از این موارد به صورت جداگانه می‌پردازیم؛ از آموزش بسته شبکه شروع می‌کنیم: تابع زیان آموزش به آهستگی کاهش می‌یابد (در تصویر هم از تفاوت کاهش شیب خط قرمز در اندازه‌نمونه 256 و خط آبی در اندازه‌نمونه 32 متوجه این موضوع می‌شوید).

دوماً گفتیم که تابع زیان حداقلی آموزش در بسته‌های بزرگتر در مقایسه با بسته‌های کوچکتر ضعیف‌تر است. برای مثال اندازه بسته شبکه 256 زیان اعتباری حداقلی 0/395 به دست می‌آورد در حالی‌که برای اندازه بسته شبکه 32 این مقدار برابر است با 0/34.

[irp posts=”22559″]

مورد سوم به زمان لازم برای آموزش هر دوره اشاره داشت که برای بسته‌های بزرگتر تا حدی کمتر است. مثلاً برای اندازه بسته شبکه 256 برابر است با 7/7 ثانیه، در حالی‌که برای اندازه بسته شبکه 32، 12/4 ثانیه است. این موضوع به ما نشان می‌دهد اگر تعداد کمی بسته شبکه بزرگ را بارگذاری کنیم، در مقایسه با زمانی‌که تعداد زیادی بسته کوچک را به صورت متوالی بارگذاری کنیم، مشکلات کمتری رخ می‌دهد. درصورتی‌که آموزش را با استفاده از چند GPU موازی‌سازی کنیم این تفاوت زمانی محسوس‌تر هم خواهد شد.

با این حال آموزش بسته‌های بزرگتر به تعداد دوره‌های بیشتری نیاز دارد که به سمت کمینه همگرا شوند (958 دوره برای اندازه بسته شبکه 256 و 158 برای اندازه بسته 32). به همین خاطر آموزش بسته‌های بزرگتر در کل بیشتر طول کشید (انداره بسته 256 تقریباً 4 برابر بیشتر از اندازه بسته شبکه 32 زمان برد). توجه داشته باشید که ما آموزش را در اینجا موازی‌سازی نکردیم. اگر این کار را انجام داده بودیم، احتمالاً زمان آموزش بسته‌های بزرگ هم به اندازه بسته‌های کوچک کوتاه می‌شد.

اگر اجرای آموزش‌ها را موازی کنیم چه اتفاقی می‌افتد؟ برای یافتن پاسخ این سؤال، با استفاده از روش انعکاسیMirrored method در نرم‌افزار تنسورفلو آموزش را بر روی 4 GPU موازی کردیم:

with tf.distribute.MirroredStrategy().scope():
   # Create, compile, and fit model
   # ...

روش انعکاسی همه متغیرهای مدل را روی هر GPU کپی کرده و محاسبه گذر به جلو و عقب Forward/backward pass computation در یک بسته شبکه را در همه GPUها توزیع می‌کند. سپس از طریق عملیات all-reduce از هر GPU گرادیان‌ها را جمع‌آوری کرده و نتایج را در کپی هر GPU از مدل پیاده می‌کند. به بیان ساده می‌توان گفت که این روش بسته شبکه را تکه تکه می‌کند و هر قطعه را به یک GPU می‌دهد.

متوجه شدیم که موازی‌سازی باعث می‌شود سرعت آموزش بر حسب دوره در خرده‌بسته‌ها کاهش یابد، در حالی‌که سرعت آموزش بسته‌های بزرگ را بالا می‌برد؛ به نحوی که برای اندازه بسته شبکه 256 زمان آموزش هر دوره از 7/70 ثانیه به 3/97 ثانیه رسید. حتی با وجود افزایش سرعت بر حسب دوره، این روش نمی‌تواند زمان آموزش کل را به سرعت اندازه بسته شبکه 32 برساند. یعنی اگر در تعداد کل دوره‌ها (958) را ضرب کنیم به مقدار تقریبی 3700 ثانیه می‌رسیم که باز هم بسیار بیشتر از زمان اندازه بسته شبکه 32 (یعنی 1915 ثانیه) است.

شکل 8 میانگین زمان بر حسب دوره در حالی‌که موازی‌سازی در 4 GPU انجام می‌گیرد.

با آنچه تاکنون خواندیم به نظر نمی‌رسد آموزش بسته‌های بزرگ به‌صرفه و منطقی باشد؛ زیرا هم زمان لازم برای آموزش آن‌ها بیشتر است و هم تابع زیان آموزش و اعتباریابی بدتری برایشان به دست می‌آید. اکنون می‌خواهیم بدانیم چرا این‌طور است و آیا راهی هست که به کمک آن بتوان این فاصله در عملکرد را جبران کرد؟

چرا عملکرد بسته‌های کوچکتر بهتر است؟

کسکار و همکارانش در مقاله خود برای این تفاوت عملکرد که بین بسته‌های کوچک و بزرگ وجود دارد یک توجیه پیدا کرده‌اند: آموزش بسته‌های کوچک تمایل دارند به هم نزدیک شده و کمینه‌های مسطح Flat minimizers را به وجود آورند که تنها در همان نزدیکی کمینه تغییرات محدودی دارند، اما بسته‌های بزرگ به هم نزدیک شده و کمینه‌های تیزSharp minimizers را ایجاد می‌کنند که می‌توانند تغییرات گسترده‌ای داشته باشند (1). کمینه‌های مسطح قابلیت تعمیم‌پذیری بهتری دارند زیرا در تغییرات بین آموزش و مجموعه آزمون‌ها قویتر عمل می‌کنند (1).

شکل 9 تصویری مفهومی از کمینه‌های مسطح و تیز برگرفته از مقاله کسکار و دستیاران

این نویسندگان همچنین به این نتیجه رسیدند که کمینه‌هایی که طی آموزش بسته‌های کوچک به دست می‌آیند، از وزن‌های تعریف شده دورتر هستند؛ به بیان دیگر، طی آموزش بسته‌های کوچک ممکن است مقداری نویز تولید شود که منجر به خروج آموزش از کمینه‌های تیز توابع زیان شده و به جای آن وارد کمینه‌های مسطحی شود که ممکن است در فاصله دورتری قرار داشته باشند.

اکنون به اعتباریابی این فرضیه‌ها می‌پردازیم.

فرضیه اول: کمینه بسته کوچک نسبت به کمینه بسته بزرگ، از وزن‌های تعریف شده فاصله بیشتری دارد

ابتدا فاصله اقلیدسیEuclidean بین وزن‌های تعریف شده و کمینه‌های هر مدل را اندازه می‌گیریم.

به‌طور کلی می‌توان گفت هرچه اندازه‌ بسته شبکه بزگ‌تر باشد، کمینه به وزن‌های تعریف‌شده نزدیک‌تر است (به استثناء اندازه بسته‌ شبکه 128 که کمینه‌ آن نسبت به اندازه بسته شبکه‌ 64، دورتر از وزن‌های تعریف‌شده قرار دارد). همان‌طور که در شکل 11 مشاهده می‌کنید، این نکته در مورد لایه‌های مختلف مدل نیز صدق می‌کند.

[irp posts=”15659″]

اما سؤال اینجاست که چرا آموزش بسته‌های بزرگ به وزن‌های تعریف‌شده نزدیک‌تر می‌شود. آیا به این خاطر است که گام‌های به‌روزرسانی آن کوچک‌تر هستند؟ برای یافتن پاسخ این سؤال فاصله‌ دور (فاصله‌ بین وزن‌های نهایی در هر دور i و وزن‌های ابتدایی در هر دور i) را در اندازه بسته‌های 32 و 256 اندازه می‌گیریم.

شکل 12 چپ: فواصل دوره‌ای برحسب اندازه راست: نسبت فواصل دوره‌ای

اولین نمودار نشان می‌دهد اندازه بسته‌های بزرگتر فواصل کمتری را در هر دوره می‌پیمایند. فاصله/دوره آموزش در اندازه بسته شبکه 32 بین 0/15 تا 0/4 است، در حالی‌که این مقدار برای بسته شبکه 256 بین 0/2 تا 0/4 است و نمودار دوم هم نشان می‌دهد که نسبت فواصل دورهای به مرور زمان افزایش می‌یابد.

حالا این سؤال مطرح می‌شود که چرا آموزش بسته‌های بزرگ فواصل کمتری را در هر دوره طی می‌کند. آیا به این خاطر این است که تعداد بسته‌های کمتر و در نتیجه تعداد کمتری به‌روزرسانی در هر دوره داریم؟ یا به این دلیل که به‌روزرسانی همه بسته‌ها فاصله کمتری می‌پیماید؟ شاید هم پاسخ در ترکیب این دو باشد.

برای یافتن جواب این سؤال باید اندازه به‌روزرسانی هر بسته شبکه را بسنجیم.

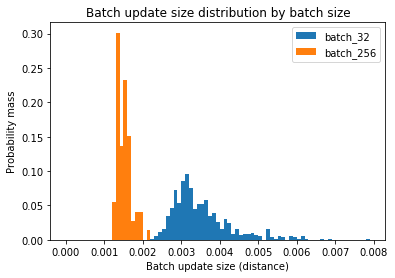
شکل 13 توزیع اندازه‌های به‌روزرسانی بسته‌ها

(میانه به‌روزرسانی بسته برای اندازه بسته 32= 3.3e-3

میانه به‌روزرسانی برای اندازه بسته 256= 1.5e-3)

همان‌طور که مشاهده می‌کنید به‌روزرسانی هر بسته شبکه با اندازه آن نسبت عکس دارد (یعنی برای بسته‌های بزرگتر، کوچکتر است). دلیل آن چیست؟

برای درک بهتر این رفتار یک سناریوی ساختگی را مثال می‌زنیم: دو بُردار گرادیانGradient vector به نام‌های a و b داریم که هرکدام معرف گرادیان یک نمونه آموزشی هستند. حال توضیح می‌دهیم چطور میانگین اندازه به‌روزرسانی بسته برای اندازه بسته شبکه 1 با همین مقدار برای اندازه بسته شبکه 2 مقایسه می‌شود.

شکل 14 مقایسه بین مراحل به‌روزرسانی بین اندازه بسته‌ 1 (a+b) و اندازه بسته 2 ((a+b)/2).

اگر بسته‌ای با اندازه یک انتخاب کنیم، در جهت a و سپس b پیش رفته‌ایم و در نهایت به نقطه‌ای می‌رسیم که با a+b نشان داده شده است (از نظر فنی می‌توان گفت که گرادیان برای بردار b بعد از اجرای a مجدداً محاسبه خواهد شد؛ اما فعلاً به سراغ این نکته نمی‌رویم). این جریان منجر به این می‌شود که میانگین اندازه به‌روزرسانی بسته،(( +)/2) شود (که جمع اندازه‌های به‌روزرسانی بسته‌هاست تقسیم بر تعداد به‌روزرسانی بسته‌ها).

از سوی دیگر اگر از اندازه بسته 2 استفاده کنیم، به‌روزرسانی بسته توسط بردار ((a+b)/2) نشان داده می‌شود (بردار قرمز در شکل 14) و بنابراین میانگین اندازه به‌روزرسانی بسته برابر می‌شود با $|\frac{a+b}{2}|/1=|a+b|/2$ حالا دو اندازه میانگین به‌روزرسانی بسته‌ها را با هم مقایسه کنیم:

شکل 15 مقایسه‌ میانگین اندازه‌ به‌روزرسانی برای اندازه بسته 1 و 2

در خط آخر معادله بالا از نامعادله مثلثی Triangle inequality استفاده کردیم تا نشان دهیم میانگین اندازه به‌روزرسانی برای اندازه بسته شبکه 1 همیشه برابر با همین مقدار برای اندازه بسته شبکه 2 یا بزرگتر از آن است.

به بیان دیگر برای اینکه میانگین اندازه برای اندازه بسته 1 و اندازه بسته شبکه 2 برابر باشد، بردارهای a و b باید هم‌جهت باشند ( $|a|+|b|=|a+b|$ ). همین منطق را می‌توان برای n بردار نیز پیاده کرد؛ بدین معنی که هرگاه همه n بردار هم‌جهت باشند، میانگین اندازه‌های به‌روزرسانی‌های بسته برای اندازه بسته شبکه 1 و اندازه بسته شبکه n برابر خواهد بود. با این حال این حالت به‌ندرت پیش می‌آید، زیرا احتمال اینکه بردارهای گرادیان همگی یک جهت داشته باشند پایین است.

با در نظر گرفتن معادله به‌روزرسانی خرده بسته می‌توان گفت زمانی‌که اندازه بسته شبکه $B_{k}$ را افزایش دهیم، بزرگی مجموع اندازه‌های گرادیان‌ها نیز، هرچند با سرعت کمتر، افزایش می‌یابد. دلیل آنچه گفته شد این است که بردارهای گرادیان جهت‌های متفاوتی دارند و بنابراین افزایش دوبرابری اندازه بسته شبکه (که تعداد بردارهای گرادیانی است که با هم جمع می‌شوند) مقدار مجموع این بردارها را به دو برابر افزایش نخواهد داد. علاوه بر این از آنجایی که هم‌زمان داریم بر مخرجی تقسیم می‌کنیم که دوبرابر بزرگتر شده، مقدار به‌روزرسانی کمتر هم خواهد شد.

این توضیحات می‌تواند این مسئله را نیز روشن کند که چرا اندازه به‌روزرسانی بسته برای اندازه بسته‌های بزرگتر، کوچکتر است. یعنی مجموع بردارهای گردیان بیشتر می‌شود، اما نمی‌تواند مخرج بزرگتر شده $B_{k}$ را جبران کند.

[irp posts=”23025″]

فرضیه دوم: آموزش بسته کوچک کمینه‌های مسطح‌‌تری به دست می‌دهد

حالا می‌خواهیم مقدار تیزی کمینه‌ها را اندازه بگیریم و این گفته را که آموزش بسته‌های کوچک کمینه‌های مسطح‌تر به دست می‌دهد، بیازماییم (توجه داشته باشید که این فرضیه بدون تأیید فرضیه اول نیز موجودیت دارد و به یکدیگر وابسته نیستند). بدین منظور دو روش را از مقاله کسکار و دستیارانش وام گرفته‌ایم.

در روش اول تابع زیان آموزش و اعتباریابی را برای کمینه‌های دو اندازه بسته شبکه 32 و 256 رسم می‌کنیم. فرمول مربوطه بدین صورت است:

شکل 17 درون‌یابی بین کمینه اندازه بسته‌ کوچک و بزرگ منبع: کسکار و دستیاران

در این فرمول مربوط به کمینه بسته بزرگ و مربوط به بسته کوچک است. هم ضریبی است با مقدار بین 1- تا 2.

شکل 18 درون‌یابی خطی بین کمینه‌ بسته‌ کوچک (∝=0) و بسته‌ بزرگ (∝=1) کمینه‌ بسته‌ بزرگ بسیار تیزتر است.

همان‌طور که در نمودار بالا مشاهده کردید کمینه بسته کوچک ( $\alpha =0$ ) از کمینه بسته بزرگ ( $\alpha =1$ ) خیلی مسطح‌تر است (کمینه بسته بزرگ تغییرات تیزتری دارد).

این روش، راه ساده‌انگارانه‌ای برای اندازه‌گیری تیزی است، زیرا فقط یک جهت را در نظر می‌گیرد. به همین دلیل هم کسکار و همکارانش در مقاله خود معیاری برای سنجش تیزی ارائه دادند که میزان تغییرات تابع زیان در همسایگی یک کمینه را اندازه می‌گیرد. در این روش ابتدا این همسایگی را با استفاده از فرمول زیر محاسبه می‌کنیم:

شکل 19 کادر محصورشده‌ای که در آن تابع زیان بیشینه می‌شود. منبع: کسکار و همکاران

در این فرمول اپسیلون پارامتری است که اندازه همسایگی را تعریف می‌کند و x نشان‌دهنده کمینه است (وزن‌ها).

در قدم بعدی معیار تیزی را به‌عنوان تابع زیان بیشینه در همسایگی کمینه که پیشتر اندازه گرفتیم، تعریف می‌کنیم.

شکل 20 تعریف معیار تیزی منبع: کسکار و همکاران

در این معادله f تابع زیانی است که ورودی آن وزن‌ها هستند.

با توجه به تعریفی که بالا از معیار تیزی ارائه شد می‌توانیم میزان تیزی کمینه‌ها را برای بسته‌های گوناگون، با مقدار اپسیلون 1e-3 محاسبه کنیم.

بر این اساس می‌توان گفت همان‌طور که در نمودار نشان داده شده، کمینه‌های بسته‌های بزرگ تیزتر هستند.

در آخر می‌خواهیم کمینه‌ها را با تصویرسازی تابع زیانی که از نظر فیلترها نرمال‌سازی شده، نشان دهیم. این نوع نمودار دو جهت را به صورت تصادفی انتخاب می‌کند که ابعاد یکسانی را به‌عنوان وزن‌های مدل خود دارند و سپس هر فیلتر کانولوشن نرمال‌سازی می‌شود (در لایههای FC به جای فیلتر از نورون استفاده می‌شود)، بدین منظور که بتوان در وزن‌های مدل، یک نرم (هنجار) یکسان را به‌عنوان فیلتر داشت. بدین ترتیب می‌توانیم اطمینان حاصل کنیم که تیزی یک کمینه تحت تاثیر بزرگی وزن‌هایش قرار نمی‌گیرد. سپس تابع زیان درراستای این دو جهت به صورتی رسم می‌شود که مرکز نمودار کمینه موردنظر باشد.

شکل 22 نمودار نرمال‌سازی شده بر اساس فیلتر D2 برای اندازه بسته‌ 32 (تصویر سمت چپ) و اندازه‌ بسته‌ 256 (تصویر سمت راست)

با مشاهده نمودارهای کانتور متوجه می‌شویم که تابع زیان کمینه‌های بسته‌های بزرگ تغییرات شدیدتری دارد.

آیا می‌توانیم با افزایش نرخ یادگیری عملکرد بسته‌های بزرگ را بهبود ببخشیم؟

در فرضیه اول دیدیم که هم اندازه به‌روزرسانی و هم فراوانی به‌روزرسانی بر حسب دوره در بسته‌های بزرگ پایین‌تر بودند و در فرضیه دوم هم دریافتیم بسته‌های بزرگتر نمی‌توانند مانند بسته‌های کوچک منطقه بزرگی را جستجو کنند. با این حال سوالی که مطرح می‌شود این است که آیا می‌توانیم با افزایش نرخ یادگیری، عملکرد بسته‌های بزرگ را بهبود ببخشیم؟

قانون مقیاس‌پذیری خطی: زمانی‌که اندازه خرده بسته در k ضرب شده، نرخ یادگیری را هم در k ضرب می‌کنیم.

می‌خواهیم این روش را برای اندازه بسته‌های 32، 64، 128 و 256 امتحان کنیم. از نرخ یادگیری پایه 0/01 برای اندازه بسته شبکه 32 استفاده می‌کنیم و این مقدار را برای سایر بسته‌ها هم به همین نسبت محاسبه می‌کنیم.

شکل 23 آموزش و اعتباریابی توابع زیان برای اندازه بسته‌های متفاوت با نرخ‌های یادگیری تطابق یافته

شکل 24 توابع زیان حداقلی آموزش و اعتباریابی برای اندازه بسته‌های متفاوت

دریافتیم که سازگار کردن نرخ یادگیری، تفاوت بین عملکرد بسته‌های کوچک و بزرگ را از بین می‌برد. بدین ترتیب برای تابع زیان اعتباریابی اندازه بسته 256 مقدار 0/352 به دست می‌آید (به جای 0/395) و به مقدار به دست آمده برای اندازه بسته 32 که 0/345 است نزدیکتر می‌شود.

سؤالی که مطرح می‌شود این است که افزایش نرخ یادگیری چطور بر زمان آموزش تأثیر می‌گذارد؟ از آنجایی که آموزش بسته‌های بزرگ به تعداد تکرارهای لازم برای آموزش بسته‌های کوچک نزدیک تقریباً شده، مدت زمان لازم برای آموزش کمتر می‌شود (در نمودار سمت چپ تصویر پایین قابل مشاهده است)؛ به نحوی که برای اندازه بسته 256، به 2197 ثانیه می‌رسد که به زمان 3156 ثانیه‌ای اندازه بسته 32 نزدیکتر است. در صورتی که از موازی‌سازی بر روی 4 GPU استفاده کنیم، این افزایش سرعت ملموس‌تر هم خواهد بود.

شکل 25 چپ: تعداد دوره‌های آموزشی لازم تا زمانی که تابع زیان اعتباریابی هم‌گرا می‌شود. راست: زمان آموزش کلی موردنیاز تا زمان همگرایی.

آیا آن‌چه گفتیم بدین معنی است که حالا دیگر اندازه بسته‌های بزرگ به سمت کمینه‌های مسطح همگرا می‌شوند؟ اگر از مقادیر تیزیSharpness scores نموداری تهیه کنیم، درمی‌یابیم که این مسئله درست بوده و سازگار کردن نرخ یادگیری منجر به مسطح شدن کمینه‌های اندازه بسته‌های بزرگ می‌شود.

شکل 26 مقایسه‌ تیزی کمینه‌ها همراه و بدون تطبیق نرخ یادگیری

نکته جالب اینجاست که با اینکه تطبیق نرخ یادگیری باعث مسطح‌تر شدن کمینه‌های بسته‌های بزرگ می‌شود، این کمینه‌ها (بین 4-7) هنوز نسبت به بسته‌های کوچک (1.14) تیزتر هستند. چرایی این مسئله پرسشی است که تحقیقات آینده باید به آن بپردازند.

[irp posts=”15709″]

آیا تعداد اجراهای آموزشی بسته‌های بزرگ به اندازه بسته‌های کوچک از وزن‌های تعریف‌شده فاصله دارند؟

شکل 27 فاصله از وزن‌های تعریف شده برای اندازه بسته‌های متفاوت، قبل و بعد از تطبیق نرخ یادگیری

پاسخ این سؤال مثبت است. با توجه به نمودار بالا می‌توان گفت سازگاری نرخ یادگیری تفاوت اندازه بسته‌های کوچک و بزرگ را از نظر فاصله آن‌ها از وزن‌های تعریف شده کاهش می‌دهد (اندازه بسته 128 از این روند پیشروی نمی‌کند و افزایش نرخ یادگیری در آن باعث کاهش فاصله می‌شود؛ این مسئله هم نیازمند تحقیقات بعدی است).

آیا آموزش بسته‌های کوچک همیشه بهتر از آموزش بسته‌های بزرگ عمل می‌کند؟

با توجه به یافته‌های بالا و پیشینه پژوهش‌های انجام شده در این حوزه، اینطور انتظار می‌رود که در صورت ثابت نگه داشتن نرخ یادگیری، آموزش بسته‌های کوچک همیشه از آموزش بسته‌های بزرگ عملکرد بهتری داشته باشند. اما واقعیت چیز دیگری است. برای مثال زمانی که از نرخ یادگیری 0/08 استفاده می‌کنیم این توابع به دست می‌آید:

شکل 28 تابع زیان اعتباریابی با نرخ یادگیری بالاتر بر اساس اندازه‌ بسته

همان‌طور که مشاهده می‌کنید اندازه بسته شبکه 64 عملکرد بهتری از اندازه بسته شبکه 32 دارد! به این خاطر که نرخ یادگیری و اندازه بسته‌ها ارتباط نزدیکی با یکدیگر دارند؛ بدین صورت که اندازه بسته‌های کوچکتر زمانی بهترین عملکرد را از خود نشان می‌دهند که نرخ یادگیری هم پایین باشد و اندازه بسته‌های بزرگ زمانی که نرخ یادگیری بالا باشد. این پدیده در شکل زیر ترسیم شده است:

شکل 29 تأثیر نرخ یادگیری بر تابع زیان اعتباریابی برای اندازه بسته‌های متفاوت

همان‌طور که می‌بینید نرخ یادگیری 0/01 برای اندازه بسته 32 و نرخ یادگیری 0/08 برای اندازه بسته‌های دیگر بهتر است.

بنابراین اگر با وجود نرخ یادگیری یکسان، اندازه بسته‌های بزرگ عملکرد بهتری از اندازه بسته‌های کوچک دارند، می‌تواند به این دلیل باشد که نرخ یادگیری بزرگتر از میزان بهینه برای اندازه بسته‌های کوچک است.

نتیجه‌گیری

معنای همه آنچه گفته شد چیست؟ از همه این طرح‌ها و آزمایشات چه نتیجه‌ای می‌توان گرفت؟

قانون مقیاسپذیری خطی: زمانی که اندازه خرده‌بسته در k ضرب می‌شود، نرخ یادگیری را هم در k ضرب می‌کنیم. با اینکه معمولاً مشاهده می‌کنیم اندازه بسته‌های بزرگتر عملکرد ضعیفتری دارند، با افزایش نرخ یادگیری می‌توانیم عمده این تفاوت را از بین ببریم. همان‌طور که گفتیم این موضوع بدین خاطر است که اندازه بسته‌های بزرگ، به دلیل رقابت گرادیانی Gradient competition بین بردارهای گرادیانِ یک بسته شبکه، به‌روزرسانی‌های بسته‌های کوچکتر را به کار می‌برند.

اگر نرخ یادگیری مناسبی انتخاب کنیم، سرعت آموزش اندازه بسته‌های بزرگتر، به‌خصوص در صورتی که موازی‌سازی رخ داده باشد، بیشتر خواهد شد. در کار با بسته‌های بزرگتر با محدودیت کمتری از جانب به‌روزرسانی‌های SGD روبرو خواهیم بود، زیرا با مشکلاتی که بارگذاری متوالی تعداد زیادی بسته کوچک در حافظه به همراه دارد روبرو نخواهیم بود. علاوه بر این قادر خواهیم بود محاسبات را در میان نمونه‌های آموزشی موازی‌سازی کنیم.

بااین‌حال زمانی که نرخ یادگیری برای سازگاری با اندازه بسته‌های بزرگ افزایش نیافته باشد، زمان لازم برای آموزش می‌تواند حتی از بسته‌های کوچک هم بیشتر شود. زیرا به تعداد دوره‌های بیشتری برای همگرا شدن نیاز دارد. بنابراین لازم است نرخ یادگیری را سازگار کنیم تا منجر به افزایش سرعت اندازه بسته های بزرگتر و موازی‌سازی شویم.

حتی در صورتی که از نرخ یادگیری سازگار شده استفاده کنیم، اندازه بسته‌های بزرگ تا حدودی عملکرد ضعیف‌تری را در آزمایشات ما از خود نشان دادند. با این حال برای تصمیم‌گیری قطعی در این مورد نیاز به داده‌های بیشتری خواهد بود. هنوز هم بین عملکرد اندازه بسته کوچک (تابع زیان اعتباریابی= 0/343) و اندازه بسته بزرگ (تابع زیان اعتباریابی=0/352) تفاوت اندکی وجود دارد. برخی معتقدند بسته‌های کوچک نوعی خاصیت تنظیم‌کنندگی دارند، زیرا به به‌روزرسانی‌ها نویز وارد می‌کنند و باعث می‌شوند آموزش از کمینه‌های محلی زیربهینهBasins of attraction od suboptimal local minima فراتر رود (1). با این وجود یافته‌های این آزمایشات نشان می‌دهد تفاوت بین عملکردهای این بسته‌ها نسبتاً کم است (یا لااقل در این داده‌های این دیتاست این‌طور بوده است). بدین ترتیب می‌توان گفت اگر نرخ یادگیری مناسب اندازه بسته را پیدا کنید، می‌توانید بر سایر جنبه‌های آموزش تمرکز کنید که می‌توانند تأثیر بیشتری بر عملکرد داشته باشند.