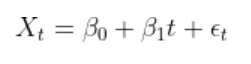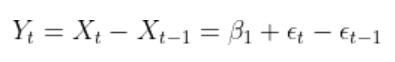راهنمای کامل سری های زمانی
در این مقاله به سؤالات زیر در خصوص سری های زمانی پاسخ میدهیم:
سریزمانی چیست؟
هدف اصلی سریزمانی چیست؟
سریزمانی چه تفاوتی با رگرسیون دارد؟
چگونه به صورت ریاضیاتی سری زمانی را مدل کنیم؟
چرا باید سریزمانی مانا باشد؟
مدلسازی ARIMA چیست؟
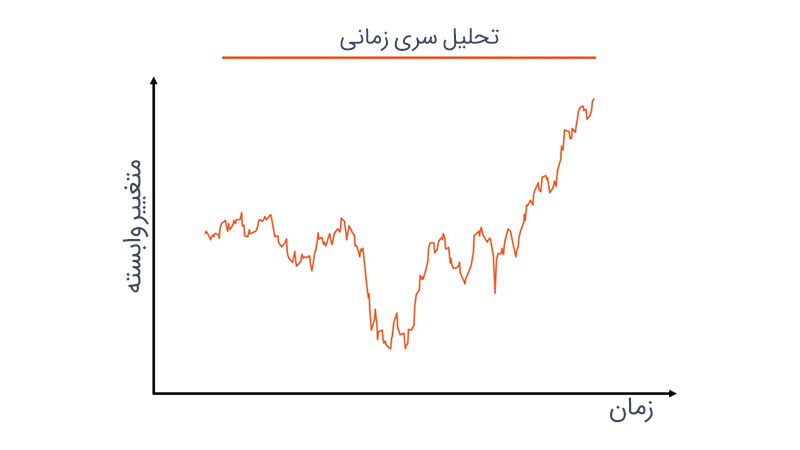
سری زمانی چیست؟
به دنبالهای از دادهها که در بازهای از نقاط زمانی گسسته توزیع شدهاند، سری زمانی میگویند.
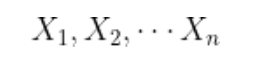
در اصطلاح احتمال، X «متغیر تصادفی» نام دارد.
سریزمانی یکی از موارد کاربردِ فرایند تصادفی در احتمال است.
هدف اصلی تحلیل سریزمانی چیست؟
هدف اصلی تحلیل سریزمانی پیشبینی است که با اندازهگیری و تخمین وابستگی بین نقطهدادهها به دست میآید.
سریزمانی چه تفاوتی با رگرسیون معمول دارد؟
فرمول رگرسیون:
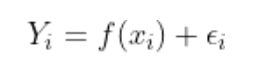
یکی از مفروضههای اصلی رگرسیون این است که موارد خطا مستقل از یکدیگر هستند و بهتبع آن نقطهدادهها نیز مستقل هستند (مانند نویز سفید).
اما سریزمانی بر این مفروضه استوار است که در گذر زمان خطاها به یکدیگر وابسته هستند؛
بنابراین، تکنیکهای متداول رگرسون در تحلیل سری های زمانی کاربردی ندارد.
چگونه به صورت ریاضیاتی سری زمانی را مدل کنیم؟
برای مدلسازی سریزمانی به زبان ریاضی، به موارد زیر احتیاج داریم
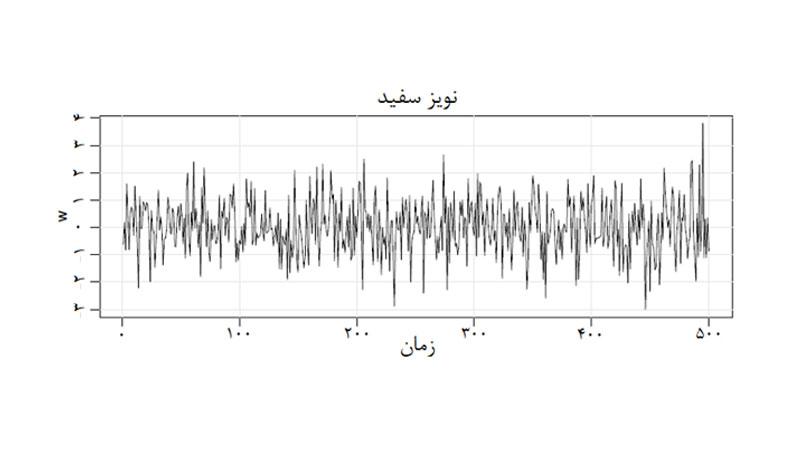
1- نویز سفید (برای مدلسازی توابع تصادفی)
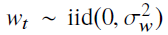
نویز سفید در طیف زمان به چه شکلی است؟
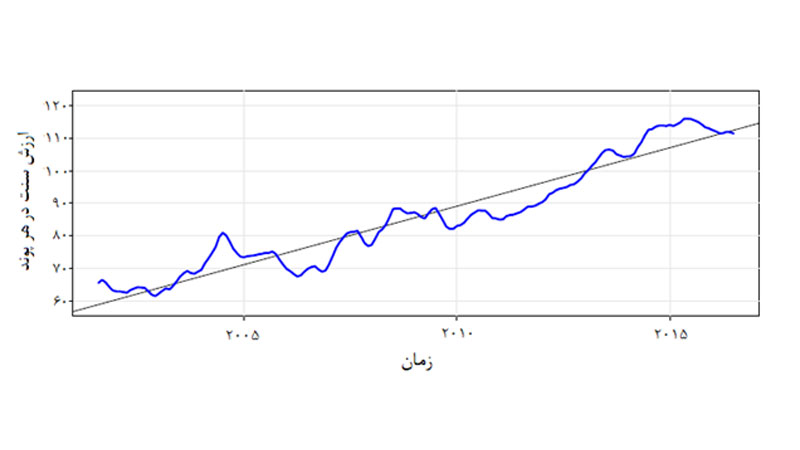
2- روند، نوسانات فصلی، و روندزدایی سریزمانی
منظور از روند تابع f(x) است. روند رفتار کلی سریزمانی را نشان میدهد.
با محاسبات ریاضی میتوان روند سریزمانی را مشخص کرد.
روابط روند ممکن است بسیار پیچیده باشد، زیرا این احتمال وجود دارد که یک سریزمانی به سریزمانی دیگری وابسته باشد؛ به این ترتیب سریزمانی علاوه بر مؤلفههای اضافی روند خود به دلیل وابستگی به دیگر سری های زمانی ممکن است مؤلفههای دیگری نیز داشته باشد.
چگونه میتوان این مشکل را حل کرد؟
برای حل پیچیدگی روند لازم است «روندزدایی» کرده، یعنی روند را حذف کنیم و باقیمانده را تحلیل کنیم.
مهمترین قسمت تحلیل سریزمانی مدلسازی روند نیست بلکه مدلسازی خطاهای وابسته به آن است.
در ادامه یکی از روشهای رفع پیچیدگی روند را توضیح میدهیم.
- تفاضلگیری
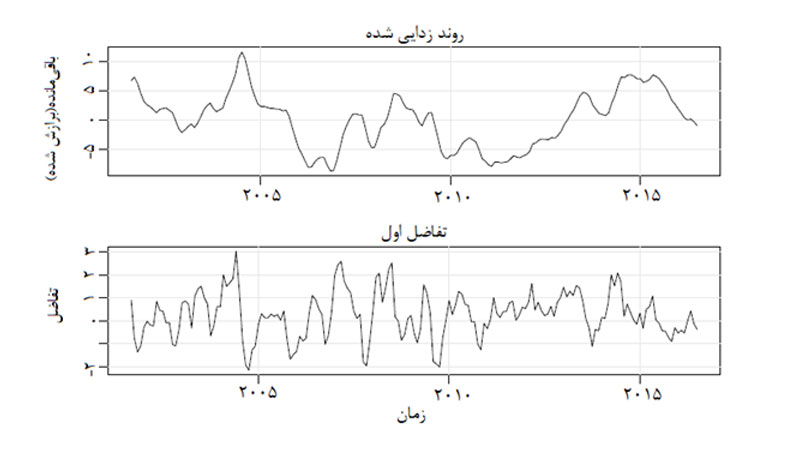
اکنون با کم کردن معادله روند و با تفاضلگیری، روند را حذف میکنیم.
همانطور که مشاهده میکنید روند همچنان دارای نظم است (با معادله خطی) در حالی که تفاضل اول همانند خطا تصادفی است.
علت تصادفی بودن باقیمانده این است که با تفاضل، نوسانات فصلی سریزمانی را نیز لحاظ کردهایم.
این کار جنبه I در مدل ARIMA را شکل میدهد. مبحث ARIMA را در نوشتاری دیگر بهطور کامل توضیح خواهیم داد.
پس از روندزدایی کُلِ سریزمانی، باقیمانده یا خطاهای نمونه بر جا میمانند که ساختاری وابسته و ویژگیهای خوبی برای بررسی دارد.
3- ساختار وابستگی خطای نقطهدادهها (وجهه تمایز با رگرسیون)
همانند آمار کلاسیک و با استفاده از مفاهیم کوواریانس و همبستگی، میتوان با انجام محاسبات آماری نشان داد که بین خطاهای دو نقطهداده وابستگی وجود دارد.
تابع کوواریانس خودکار
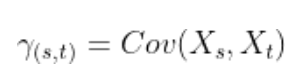
تابع کوواریانس خودکار وابستگی بین خطاهای دو نقطهداده را در زمانهای t و s محاسبه میکند.
کوواریانس ممکن است بسیار بزرگ باشد. بنابراین لازم است آن را نرمالسازی کرده و به تابع خودهمبستگی تبدیل کنیم.
تابع خودهمبستگی
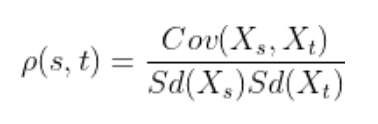
تابع خودهمبستگی (ACF) وابستگی نرمالِ بین خطاهای دو نقطهداده را در زمانهای t و s محاسبه میکند. مقدار این تابع بین 1 و 1- است.
توجه داشته باشید که باید ACF را از دادهها و با استفاده از ضریب همبستگی بهدستآمده برای نمونه تخمین بزنیم.
4- ویژگیهای خطای خوب (قابل پیشبینی)در دادههای سریزمانی
خطای خوب یا بهعبارتی خطای قابل پیشبینیِ سری های زمانی «مانا» است.زمانی میتوان گفت یک سریزمانی (یا بهعبارتی خطاهای یک سریزمانی) بهخوبی رفتار کرده است که تمام مجموعههای آن در گذر زمان بهلحاظ آماری بدون تغییر بماند (مانایی).
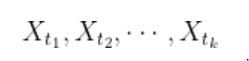
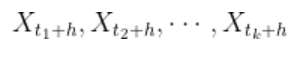
این دو مجموعه از نقطهدادهها باید بهلحاظ آماری رفتار یکسانی داشته باشند (یا بهعبارتی مانا باشند).
اما این امر در دنیای واقعی بهندرت اتفاق میافتد و بررسی کردن آن نیز دشوار است.
بنابراین دو شرط زیر را مدنظر قرار میهیم که به موجب آنها میتوانیم رفتار گشتاور مرتبه اول (میانگین) و گشتاور وابستگی مرتبه دوم (کوواریانس) را بررسی کنیم.
- تابع مقدار میانگین باید در گذر زمان ثابت باشد و با کم کردن یک مقدار ثابت از آن، بتوانیم همواره آن را صفر کنیم.
- تابع کوواریانس خودکارِ (ساختار وابسته) دو نقطهداده در زمانهای t و s، باید فقط در وقفه زمانی |t-s| وابسته باشند.
روند بهخودیخود مانا نیست، زیرا در روند تابع میانگین با گذر زمان تغییر میکند. بنابراین برای رسیدن به مانایی باید آن را روندزدایی کنیم.
برقراری دو شرط بالا نشان میدهد که عملکرد تابع وابستگی خطا مبتنی بر ویژگی رفتاری مناسب، یعنی همان مانایی است.
در ادامه روشهای مختلف و جالبی برای مدلسازی وابستگی با کمک ACF ارائه خواهیم کرد.
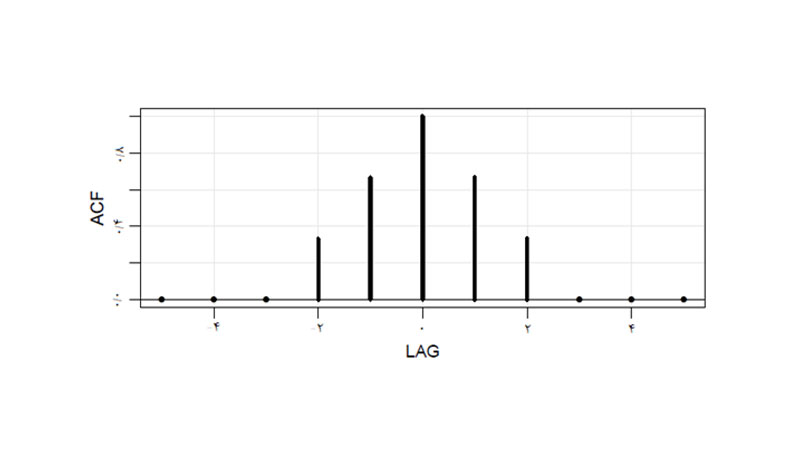
در موارد مانا، تابع ACF به تابع وقفه زمانی (h) تبدیل میشود.
تابع خودهمبستگی در گذر زمان کاهش مییابد.
کاهش تابع همبستگی به معنای آن است که به طور شهودی به این معنی است که نقاط داده دور از هم به سختی مرتبط و وابسته به یکدیگر هستند.
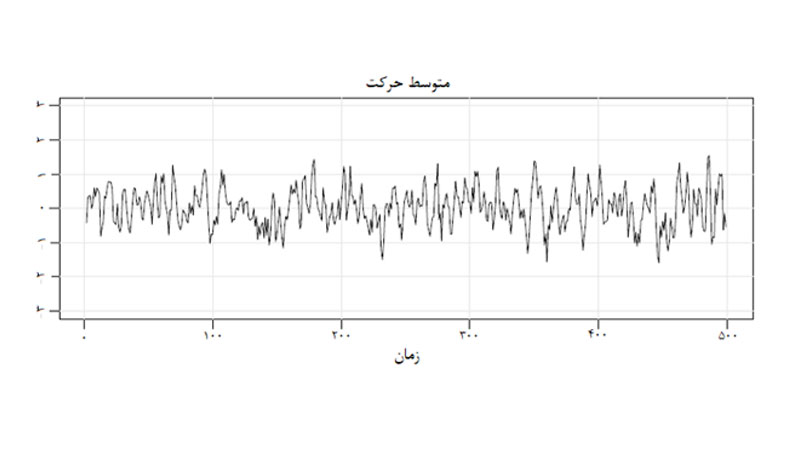
چرا باید سریزمانی مانا باشد؟
مانایی سری های زمانی کمک میکند ساختار وابستگی و رفتار میانگین تمام نمونههای ممکن را بهطور تقریبی محاسبه کنیم.
تخمین ساختار وابستگی و میانگین مجموعهها کمک میکند بفهمیم نقطهدادهها (بر حسب وقفههای زمانی) تا چه حد با یکدیگر ارتباط دارند. همین مباحث مبنای AR و MA در مدلهای ARIMA را تشکیل میدهد.
خلاصه مطالب
سریزمانی = روند + نوسانات فصلی + خطای وابستگی
گام اول:
دادهها را به دادههای مانا تبدیل کنید.
- در روندهای چندجملهای میتوانیم برای روندزدایی چندین مرتبه تفاضلگیری کنیم.
- در روندهای نمایی باید قبل از تفاضلگیری روند را ابتدا با یک تبدیل غیرخطی به یک روند چند جملهای تبدیل کنیم.
- روشهای دیگری نیز برای روندزدایی وجود دارد.
- روشهای ساده دیگری برای درک روند و سپس روندزدای آن وجود دارد (مانند روش برآوردگر نادریا واتسون).
- بررسی نمودارهای مختلف سری های زمانی به شما کمک میکند، تا درک بهتری از آنها داشته باشید. برای بررسی مانایی، اطلاعات آماری آنها را بررسی کنید.
این موارد را بهطور کامل در مقاله دیگری توضیح خواهیم داد. در ادامه دادهها را برای درک ساختار وابستگی ِگام دوم آماده میکنیم.
گام دوم:
مدلسازی و پیشبینی ساختار وابستگیِ خطاها
مدلسازی وابستگی با دو روش معروف زیر صورت میگیرد:
- AR
- MA
خلاصهای از مدل ARIMA
- از طریق تبدیل و تفاضلگیری دادهها را به دادههای مانا تبدیل کنید.
- با اجرای مدلهای AR و MA ساختار وابستگی سریزمانی تفاضلگیریشده را محاسبه کرده و پیشبینی را انجام دهید.
- به عبارت دیگر: AR + I + MA = ARIMA