چرا قضیه حد مرکزی برای متخصصین علوم داده اهمیت دارد؟
قضیه حد مرکزی Central Limit Theorem در کانون استنباط آماری Statistical inference قرار دارد که متخصصین علوم داده و تحلیلگران داده هر روز با آن سر و کار دارند.
در مقاله پیشرو به مطالعه و بررسی قضیه حد مرکزی و چیستی آن میپردازیم؟ دلایل اهمیت آن چیست؟ قضیه حد مرکزی چه تفاوتی با قانون اعداد بزرگ Law of Large Numbers دارد؟
قضیه حد مرکزی چیست؟
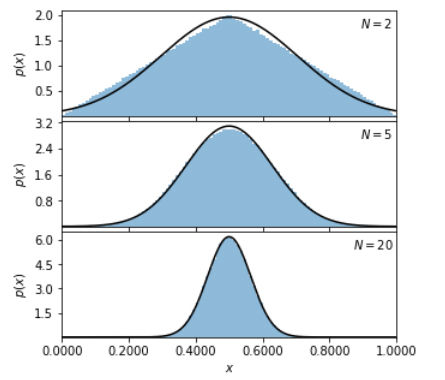
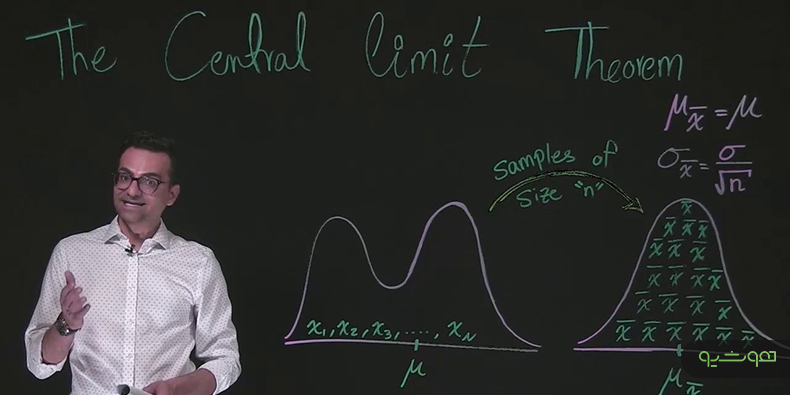
یکی از قضیههای مهم و کاربردی در آمار و احتمالات قضیه حد مرکزی است. این قضیه بیان میدارد همزمان با افزایش حجم نمونهها، توزیع میانگین (Mean) تعدادی از نمونهها به سمت توزیع گوسی میل میکند.
فرض کنید آزمایشی انجام میدهیم و در این آزمایش دادههایی به دست میآوریم و یا مشاهداتی ثبت میکنیم. با تکرار این آزمایش میتوانیم مشاهده مستقل دیگری به دست آوریم. از تجمیع کلیه این دادهها به نمونهای از مشاهدات دست پیدا میکنیم.
اگر میانگین یک نمونه را محاسبه کنیم، این میانگین نزدیک به میانگین توزیع جامعه خواهد بود. این میانگین ممکن است همیشه درست نباشد و خطا داشته باشد. در صورتیکه نمونههای مستقل زیادی داشته باشیم و میانگین آنها را محاسبه کنیم، توزیع آنها، به سمت توزیع گوسی میل میکند.
تمامی آزمایشاتی که انجام میدهیم و خروجی آن یک مشاهده است، باید به صورت مستقل انجام شود و روند انجام آنها یکسان باشد. دلیل آن هم این است که مطمئن شویم نمونه از یک جامعه آماری مشخص به دست آمده است . در اصطلاح تخصصی از این شرط با عنوان توزیع نامشخص و یا مجموعهای از گزارههای مقایسهای یاد میشود.
دلایل اهمیت قضیه حد مرکزی چیست؟
CLT بر مبنای تخمینهای (برآوردها) ما، توزیع خاصی ترسیم میکند. با استفاده از این توزیع میتوانیم صحت و درستی احتمالات برآوردی خود را بررسی کنیم. برای مثال، فرض کنید میخواهیم نتایج انتخابات را پیشبینی کنیم.
فرض کنید نتایج حاصل از یک نظرسنجی نشان میدهد که 30% از نمونههای آماری (افراد شرکتکننده در نظرسنجی) نامزد انتخاباتی A را بر نامزد انتخاباتی B ترجیح میدهند. طبیعتاً ما فقط از نمونه کوچکی از کل جمعیت نظرسنجی کردهایم و میخواهیم بدانیم آیا میشود نتایج این نظرسنجی را به کل جامعه تعمیم داد و در صورتی که امکان تعمیم نتایج به کل جمعیت وجود نداشته باشد، میخواهیم بدانیم نتایج حاصل از نظرسنجی ما چقدر خطا دارد.
در این حالت CLT به ما نشان میدهد اگر این نظرسنجی را بارها و بارها تکرار کنیم، توزیع فرضیات بعدی در کل جامعه آماری نرمال خواهد بود.
در CLT توزیع احتمالات از مرکز به سمت دُم است. به عبارت دیگر، در صورتیکه نزدیک به مرکز توزیع قرار داشته باشید، حدود دو سوم از نتایج حاصل در فاصله یک انحراف از معیار استاندارد از میانگین قرار میگیرند و حتی با تعداد نمونههای کمتر میتوانید مطمئن باشید که نتایج شما قابل تعمیم هستند.
از سوی دیگر، چنانچه در فاصله دمهای توزیع، کل نتایج حاصل در فاصله پنج انحراف معیار از میانگین قرار داشته باشند حتی اگر حجم نمونههایی که در اختیار دارید، کافی باشد باز هم نمیتوانید نتایج حاصل از نظرسنجی را به کل جامعه آماری تعمیم دهید.
چنانچه توزیعی واریانس نامتناهی داشته باشد، CLT عملکرد خوبی ندارد. چنین مواردی به ندرت رخ میدهد اما در برخی از زمینهها چنین توزیعهایی دور از ذهن نیست.
قضیه حد مرکزی چه تفاوتی با قانون اعداد بزرگ دارد؟
معمولاً افراد مبتدی CLT را با قانون اعداد بزرگ اشتباه میگیرند. CLT و LLN با یکدیگر تفاوت دارند و تفاوت کلیدی میان این دو این است که LLN به حجم یک نمونه و CLT به تعداد نمونهها بستگی دارد.
LLN بیان میدارد میانگینهای نمونه مشاهدات مستقل و نامشخص، به یک مقدار خاص متمایل است و CLT توزیع اختلاف میان میانگینهای نمونه و مقدار را ترسیم میکند.
دلایل اهمیت قضیه حد مرکزی در استنباط آماری
CLT نقش تعیینکنندهای در استنباط آماری دارد. CLT نشان میدهد برای کاهش خطای نمونهگیری، حجم نمونه را تا چه اندازه باید افزایش دهیم. خطای نمونهگیری اطلاعاتی راجع به دقت و حاشیه خطای برآوردهای آماری که بر مبنای نمونهها انجام دادهایم (برای مثال بر حسب درصد) در اختیار ما میگذارد.
از تجمیع حجم نسبتاً بالایی از متغیرهای تصادفی مستقل، یک نمونه تصادفی ایجاد میشود که توزیع آن تقریباً نرمال است.
در گذر از نمونه به جامعه، احتمال اهمیت بسزایی دارد و به زبان ساده اگر به جای مطالعه کل جامعه آماری، بخشی از آن را مطالعه کنیم و بتوانیم نتایج حاصل از آن را به کل جامعه تعمیم دهیم، از روشهایی استفاده کردهایم که موضوع استنباط آماری است. با این توصیفات چگونه میتوانیم مطمئن شویم روابطی (یا نسبتی) که در یک نمونه مشاهده کردهایم صرفاً بر پایه احتمالات نیست؟
در همین راستا آزمونهای معناداری تهیه و تدوین شدهاند تا معیارهایی معرفی کنند و ما بتوانیم بر مبنای آنها امکان تعمیم نتایج به کل جامعه آماری را بسنجیم. برای مثال، ممکن است فردی متوجه شود رابطهای منفی میان سطح تحصیلات و درآمد وجود دارد. گرچه به اطلاعات بیشتری نیاز است تا اثبات کنیم این نتیجهگیری صرفاً بر پایه احتمال نبوده ولی به لحاظ آماری اهمیت آن را هم نمیتوانیم نادیده بگیریم.
منظور از توزیع نرمال قضیه حد مرکزی چیست؟
CLT توزیع گوسی را نوعی توزیع طبیعی و حدی در نظر میگیرد و بسیاری از فرضیههای آماری را موجه میداند، برای مثال، توزیع نرمال جملههای خطا در رگرسیون خطی مستقل از متغیرهای تصادفی زیادی است که واریانس پایین و خطاهای غیرقابل تشخیص دارند و به همین دلیل انتظار میرود که توزیع آن نرمال باشد.
اگر دادههایی دارید و نمیدانید توزیع آنها به چه صورت است، میتوانید از CLT استفاده کنید و توزیع آن را نرمال فرض کنید.
نقاط ضعف قضیه حد مرکزی
یکی از نقاط ضعف CLT این است که اغلب بدون رفع و بررسی حاشیه خطا مورد استفاده قرار میگیرد و این مشکلی است که حوزه مالی مدتی با آن درگیر بوده، در این حوزه فرض بر این بوده که بازده نرمال است، در حالی که دمهای توزیع کشیده
Fat-tailed distribution بوده؛ آسیبهایی اینگونه توزیعها بیشتر از توزیعهای نرمال است.
نقض قضیه حد مرکزی
زمانیکه با مجموعهای از متغیرهای تصادفی وابسته، مجموعهای از متغیرهای تصادفی با توزیع نامشخص و یا مجموعهای از متغیرهای تصادفی وابسته با توزیع نامشخص سروکار دارید، CLT عملکرد خوبی ندارد.
نمونههای دیگری از CLT وجود دارد که در آنها لازم نیست هر دو شرط فوق رعایت شود (متغیرهای وابسته و متغیرهایی با توزیع نامشخص) . برای نمونه میتوان به قضیه لیندبرگ فلر Lindberg-Feller theorem اشاره کرد؛ در این قضیه متغیرها حتماً باید مستقل باشند اما نامشخص بودن توزیع متغیرها شرطی اساسی و ضروری نیست.
آیا در قضیه حد مرکزی فقط میانگین اهمیت دارد؟
از CLT برای استنباط میانگین استفاده میشود. CLT بیان میدارد میتوان برای میانگین (های) یک نمونه بزرگ که واریانس کوچکی دارند، توزیع نرمال در نظر گرفت. اندازه نمونه قبل از برآورد خوب است و بستگی به توزیع دارد، در نتیجه اگر داده پرت نداشته باشیم، میتوانیم از میانگین نمونه به عنوان نمونه جامعه استفاده کنیم تا احتمال خطا را به دست بیاوریم.
قضیه حد مرکزی – جزئی از طبیعت
CLT موضوعی چالشبرانگیز است. حتی با وجود اینکه میتوانیم آزمونهای زیادی بگیریم و نمونههای زیادی بیاوریم، CLT باز هم مبهم است. شاید عجب به نظر برسد که توزیع گوسی یک توزیع حدی است. اما به هر حال بخشی از طبیعت است و باید آن را بپذیریم. از این روی، توزیع گوسی تقریباً شبیه نیروی جاذبه است. هرچند انسانها CLT را اختراع نکردهاند ، اما بدون شک آن را اثبات کردهاند.
قضیه حد مرکزی در حل چه مشکلاتی میتواند به ما کمک کند؟
توزیع نرمال مدلی ساده با توزیع متقارن و با یک پیک به دست میدهد. برای از بین بردن ناهمسانی واریانس و مقایسبندی، نیاز به بازتعریف مقیاس متغیرها داریم. علاوه بر این، CLT در تشخیص تغییرات و بازتعریف متغیرها نیز کاربرد دارد. مقایسه جمعیتهایی که بر روی توزیع آنها روش انتقال انجام شده را میتوان به سادگی و با تجزیه و تحلیل واریانس مدل نرمال انجام داد. واریانس این مدل هنجار در برابر انحراف معیار مقاوم است، اما ناهمسانی واریانس بر نتایج تأثیر میگذارد).
یکی دیگر از کاربردهای رایج توزیع نرمال این است که به عنوان (هنجار) مدل خطا برای بررسی تناسب سایر مدلها استفاده میشود. به همین دلیل از مجذورات مدل مورد نظر (مدلی که آزمایش و بررسی میکنیم) استفاده میکند.
موارد کاربرد قضیه حد مرکزی در دنیای واقعی
شاید بتوان گفت CLT پرکاربردترین قضیه در تمامی علوم است. بسیاری از علوم از جمله نجوم، روانشناسی، اقتصاد و غیره به استفاده از این قضیه رغبت دارند. هر وقت دیدید در تلویزیون نتایج حاصل از یک نظرسنجی را با فاصله اطمینان گزارش میدهند، مطمئن باشید در این نظرسنجی از قضیه حد مرکزی استفاده شده است.
CLT در تمامی نمونهها، نظرسنجیها، آزمایشهای بالینی، تجزیه و تحلیلهای تجربی، آزمایش تصادفی کنترلشده Randomized intervention و غیره مورد استفاده قرار میگیرد.
نتیجهگیری
CLT ابزار قدرتمندی است و صرف نظر از اینکه داده ها از مجموعه توزیعها به دست آمدهاند یا خیر، چنانچه میانگین و واریانس آنها یکسان باشد، میتوانیم از این قضیه استفاده کنیم.
CLT بیان میدارد که میانگین نمونه به سوی میانگین جمعیت میل میکند و سپس فاصله میان آنها کم میشود تا توزیع به سمت نرمال میل کند؛ در این حالت همزمان با افزایش حجم نمونهها، واریانس آن با واریانس جمعیت برابر میشود. این موضوع در استفاده از آمار و درک طبیعت اهمیت دارد.