مدیریت دیتاست‌های نامتوازن در مسائل رده‌بندی دودویی (بخش سوم)

در مقالات قبلی این مجموعه، تکنیک‌هایی را معرفی کردیم که برای مدیریت دیتاست های نامتوازن در مسائل رده‌بندی دودویی به کار می‌روند. در قسمت اول برخی از روش‌های بازنمونه‌گیری توضیح داده شد و قسمت دوم بر اصلاح الگوریتم از طریق تغییر مقدار آستانه‌ای (نقطه‌برش) تمرکز داشت. (لینک قسمت‌های قبل در انتهای مطلب در دسترس است)

در این نوشتار که قسمت سوم است، یکی دیگر از روش‌هایی را بررسی می‌کنیم که مستقیماً بر روی خود الگوریتم مداخله می‌کند؛ این تکنیک با تابع زیان الگوریتم سروکار دارد.

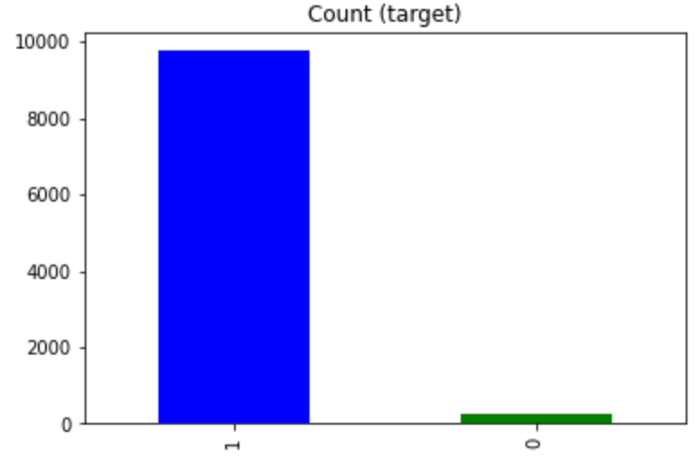
ایده‌ کلی این تکنیک، مشابه با روش نقطه‌برش است که در قسمت قبلی توضیح دادیم. اگر چنین دیتاست نامتوازنی داشته باشیم:

هدف این است که الگوریتم قادر باشد منفی‌ها (نمونه‌های کلاس 0) را نیز به‌درستی و با احتمال بالا تشخیص دهد و رده‌بندی کند، حتی اگر این کار به قیمت رده‌بندی اشتباه چند نمونه از کلاس مثبت (کلاس 1) تمام شود. این کار را می‌توان با نامتقارن کردن تابع زیان انجام داد.

در این مثال، از تابع زیان آنتروپی متقاطع دودویی استفاده می‌کنیم، چون مسئله‌ای که در دست داریم، یک مسئله‌ رده‌بندی دودویی است:

توجه داشته باشید که p(x) مقدار پیش‌بینی‌شده‌ y است. اینجا p(x) را احتمال قرارگیری نمونه در کلاس 1 در نظر می‌گیریم و احتمال قرارگیری در کلاس 0 مکمل این مقدار یعنی 1-p(x) است.

هدف این است که مثبت‌های کاذب را بیشتر از منفی‌های کاذب جریمه کنیم؛ چون می‌خواهیم الگوریتم را وادار کنیم، منفی‌های حقیقی را به‌درستی رده‌بندی کند. بدین منظور، می‌توانیم دو جزء تابع آنتروپی متقاطع را به نحوی وزن‌دهی کنیم که جزء دوم سنگین‌تر باشد:

در این معادله، w_2>w_1

برای درک بهتر تغییرات جریمه‌ مربوط به یک نمونه‌ مثبت کاذب، به تصاویر زیر دقت کنید:

یک نمونه‌ پیش‌بینی‌شده از y داریم: 8/0=p(red)؛ پس با اینکه این نمونه در واقع متعلق به کلاس 0 است، ولی در کلاس 1 زده بندی شده است (مثبت کاذب). در شکل سمت راست، جریمه‌ تابع زیان متقارن را می‌بینید که کمتر از تابع زیان نامتقارن است (61/1 < 22/3). دلیل این مسئله این است که می‌خواهیم خطای چنین رده‌بندی اشتباهی را خیلی بیشتر از خطای یک منفی کاذب جریمه کنیم.

پیاده‌سازی در پایتون

برای پیاده‌سازی در پایتون از Keras به‌عنوان یک رده بند دودویی برای داده‌های مصنوعی خود استفاده می‌کنیم. بدین ترتیب، به‌سادگی می‌توانیم هنگام کامپایل کردن مدل، یک تابع سفارشی را به‌عنوان تابع زیان وارد کنیم.

ابتدا دیتاست نامتوازن خود را تعریف می‌کنیم و آن را به دو مجموعه‌ آموزشی و آزمایشی تقسیم می‌کنیم:

from sklearn.datasets import make_classification
import pandas as pdX, y_tmp = make_classification(
    n_classes=2, class_sep=1, weights=[0.98, 0.02],
    n_informative=10, n_redundant=0,n_repeated=0, 
    n_features=10,  
    n_samples=10000, random_state=123
)#little trick for terminlogy purpose (positive class = 1, negative class = 0)y = y_tmp.copy()
for i in range(len(y_tmp)):
  if y_tmp[i]==0:
    y[i] = 1
  else:
    y[i] = 0#splittingfrom sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(
       X, y, test_size=0.33, random_state=42)from 
from sklearn.metrics import classification_report, confusion_matrix

import numpy as np
import tensorflow as tf
from tensorflow import keras
import pandas as pdmodel = keras.Sequential([
  keras.layers.Dense(
    units=36,
    activation='relu',
    input_shape=(X_train.shape[-1],)
  ),
  keras.layers.BatchNormalization(),
  keras.layers.Dense(units=1, activation='sigmoid'),
])

حال یک مدل متوالی خیلی ساده را از طریق Keras تعریف می‌کنیم.

ابتدا می‌خواهیم نتایج تابع زیان متقارن را بررسی کنیم؛ به همین دلیل، مدل را با تابع آنتروپی متقاطع دودویی استاندارد کامپایل می‌کنیم:

model.compile(
  optimizer=keras.optimizers.Adam(lr=0.001),
  loss=keras.losses.BinaryCrossentropy(),
  metrics="Accuracy"
)history = model.fit(
    X_train,
    y_train,
    epochs=20,
    validation_split=0.05,
    shuffle=True,
    verbose=0
)model.evaluate(X_test, y_test)

همان‌طور که مشاهده می‌کنید، دقت مدل 98 درصد است. بااین‌حال، همان‌طور که در مقاله‌ قبلی نشان دادیم، این می‌تواند یکی از عوارض جانبی رده‌بندی اشتباه کلاس اقلیت باشد. ماتریس درهم‌ریختگی این نتیجه را هم مشاهده می‌کنیم:

import matplotlib.pyplot as pltpreds = model.predict(X_test)
y_pred = np.where(preds>0.5,1,0)cm = confusion_matrix(y_test, y_pred)fig, ax = plt.subplots(figsize=(8, 8))
ax.imshow(cm)
ax.grid(False)
ax.xaxis.set(ticks=(0, 1), ticklabels=('Predicted 0s', 'Predicted 1s'))
ax.yaxis.set(ticks=(0, 1), ticklabels=('Actual 0s', 'Actual 1s'))
ax.set_ylim(1.5, -0.5)
for i in range(2):
    for j in range(2):
        ax.text(j, i, cm[i, j], ha='center', va='center', color='red')
plt.show()

با اینکه این الگوریتم از رگرسیون لوجیستیک بهتر است، اما همچنان 54 نمونه‌ منفی حقیقی را به اشتباه رده‌بندی کرده است! پس باید راهی برای تشخیص این نمونه‌ها پیدا کنیم. بنابراین، از رویکرد تابع زیان سفارشی استفاده می‌کنیم:

import keras.backend as Kdef weighted_binary_crossentropy(y_true, y_pred):
  weights = (tf.math.abs(y_true-1) * 59.) + 1.
  bce = K.binary_crossentropy(y_true, y_pred)
  weighted_bce = K.mean(bce * weights)
  return weighted_bce

اینجا با استفاده از آنتروپی متقاطع تعبیه‌شده (همراه کمی تغییر)، یک ترفند هوشمندانه را به کار بردیم: یک تنسور از وزن‌ها را به نحوی تعریف کردیم که ورودی‌های منفی، وزن بیشتری (=60) را به نسبت وردی های مثبت دریافت کند. دریافت کنند و بدین ترتیب، جریمه‌ رده‌بندی اشتباه آن‌ها نیز سنگین‌تر شود.

model.compile(
  optimizer=keras.optimizers.Adam(lr=0.001),
  loss=weighted_binary_crossentropy,
  metrics="Accuracy"
)model.fit(
    X_train,
    y_train,
    epochs=20,
    validation_split=0.05,
    shuffle=True,
    verbose=0
)

حال مدل را با این تابع جدید کامپایل می‌کنیم:

به ماتریس درهم‌ریختگی به‌دست‌آمده توجه کنید:

همان‌طور که ماتریس بالا نشان می‌دهد، مدل اکنون می‌تواند 57 نمونه‌ منفی (27 تا بیشتر از قبل) را به‌درستی رده‌بندی کند. می‌توانید مقادیر گوناگون و فرایندهای وزن‌دهی متفاوتی را امتحان کنید، تا به نتیجه‌ دلخواه خود برسید (که البته بستگی دارد به مسئله‌ای که در دست دارید). در ازای رسیدن به این نتیجه، چندین نمونه مثبت کاذب (317) به دست آورده‌ایم؛ اینکه این نوع رده‌بندی اشتباه (افزایش مثبت‌های کاذب) برای شما قابل‌قبول است یا خیر به مسئله‌ شما و کاربرد آن بستگی دارد.

جمع‌بندی

سفارشی کردن تابع زیان، روش خوبی برای مدیریت داده‌های نامتوازن است. البته این فرایند (همچون تغییر نقطه‌برش‌ها) هزینه‌ای دارد و آن هم کاهش دقت کلی مدل است؛ اما باید به یک نکته توجه کرد؛ آن شرکت بیمه‌ای که قرار است از این الگوریتم استفاده کند، در صورتی احساس امنیت بیشتری خواهد داشت که الگوریتم بتواند معاملات کلاهبرداری را تشخیص دهد (هر چند به قیمت رده‌بندی اشتباه چند معامله‌ واقعی باشد) یا اگر الگوریتم از نظر اسمی دقت بالایی داشته باشد، اما بیشتر معاملات کلاهبرداری را نادیده بگیرد؟

پس می‌توان گفت، ابتدا باید اولویت‌ها در مسئله‌ موجود مشخص شود و سپس راهکاری مناسب انتخاب شود.

از طریق لینک زیر می‌توانید به بخش‌های اول و دوم دسترسی داشته باشید:

مدیریت دیتاست‌های نامتوازن در مسائل رده‌بندی دودویی (بخش اول)

مدیریت دیتاست‌های نامتوزان در مسائل رده‌بندی دودویی (بخش دوم)