معرفی ده الگوریتم بهینه‌سازی گرادیان کاهشی تصادفی به همراه چیت‌شیت

الگوریتم‌های بهینه‌سازی گرادیان کاهشی تصادفی که برای یادگیری عمیق ضروری هستند

(در وبلاگ نویسنده چیت‌شیتی از بهینه‌سازها از جمله RAdam قرار دارد)

گرادیان کاهشی یک روش بهینه‌سازی است که به‌منظور یافتن کمینه‌ تابع زیان استفاده می‌شود. مدل‌های یادگیری عمیق برای به‌روزرسانی وزن‌ها طی پس‌انتشار، از این روش استفاده می‌کنند.

هدف از این نوشتار، معرفی الگوریتم‌های رایج بهینه‌سازی گرادیان کاهشی است که در چارچوب‌های محبوب یادگیری عمیق (همچون TenserFlow، Keras، PyTorch) به کار می‌روند. امیدواریم با تکنیک‌هایی که برای نام‌گذاری پارامترها و متغیرها به کار برده‌ایم، درک فرمول‌ها برای مخاطبان آسان‌تر شده باشد. در انتهای این مقاله، یک چیت‌شیت نیز درج شده است.

فرض نویسنده بر این بوده است که خوانندگان با مباحث گرادیان کاهشی و گرادیان کاهشی تصادفی تا حدودی آشنایی دارند.

در این لینک، دمویی از کاربرد بهینه‌سازهای گرادیان کاهشی (مثل SGD، مومنتوم و Adam) در یک مسئله‌ رگرسیون خطی را مشاهده می‌کنید.

کارکرد بهینه‌سازهای گرادیان کاهشی تصادفی

در نسخه‌ ساده‌ SGD (گرادیان کاهشی تصادفی)، برای به‌روزرسانی وزن‌ها، یکی از عوامل مربوط به گرادیان (یعنی  یا نرخ یادگیری) از وزن‌های فعلی تفریق می‌شود.

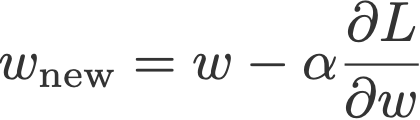
متغیرهای معادله‌ بالا را عموماً به نام بهینه‌سازهای گرادیان کاهشی تصادفی می‌شناسند. سه تفاوت اساسی بین این بهینه‌ساز‌ها وجود دارد:

1. تغییر « متن artificial »  (∂L/∂w)

برخلاف روش گرادیان کاهشی تصادفی ساده که برای به‌روزرسانی وزن‌ها تنها از یک گرادیان استفاده می‌کند، در اینجا چندین گرادیان را با هم ادغام می‌کنیم. به بیان دیگر، در این بهینه‌سازها از میانگین متحرک نمایی گرادیان‌ها استفاده می‌شود.

• تغییر « مؤلفه‌ گرادیانیGradient component » (α)

در اینجا نرخ یادگیری ثابت نگه داشته نمی‌شود، بلکه مقدار آن هماهنگ با اندازه‌ گرادیان(ها) انطباق می‌یابد.

• موارد (۱) و (۲)

هردو مؤلفه‌ گرادیانی و نرخ یادگیری به کار می‌روند.

همان‌طور که در بخش‌های بعدی مقاله بیان خواهیم کرد، این بهینه‌سازها سعی دارند مقدار اطلاعاتی را که برای به‌روزرسانی وزن‌ها به کار می‌رود، ارتقا دهند و بدین منظور، علاوه بر گرادیان‌های موجود، از گرادیان‌های گذشته (و آینده) نیز استفاده می‌کنند.

در جدول زیر، مؤلفه‌های به‌کاررفته در هر کدام از بهینه‌سازها را به‌صورت خلاصه به نمایش گذاشته‌ایم:

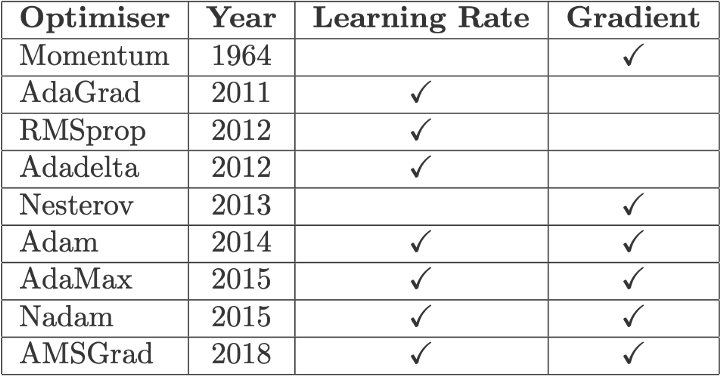
فهرست محتوا

1. گرادیان کاهشی تصادفی
2. ممنتومMomentum
3. AdaGrad
4. RMSprop
5. Adadelta
6. NAG
7. AdaMax
8. Nadam
9. AMSGra

ضمیمه ۱: چیت‌شیت

ضمیمه ۲: اطلاعات بیشتر

ضمیمه ۳: مقایسه‌ زمان‌بندهای نرخ یادگیریLearning rate schedulers با بهینه‌سازهای گرادیان کاهشی تصادفی

نمادها

• t: گام زمانیTime step
• w: وزن/ پارامتری که می‌خواهیم به‌روزرسانی کنیم
• : نرخ یادگیری
• ·        ∂L/∂w: گرادیان L (تابع زیانی که باید نسبت به w به حداقل برسانیم)

علاوه بر این‌ها، نویسنده نمادها و حروف یونانی به‌کاررفته در مقاله‌ اصلی را نیز استانداردسازی کرده‌ است، تا درک مطالب برای خوانندگان آسان‌تر شود؛ به همین دلیل، ممکن است این نمادها نسبت به مقالات و مطالب دیگری که مطالعه می‌کنید متفاوت باشند.

1. گرادیان کاهشی تصادفی (SGD)

همان‌طور که پیش‌تر توضیح داده شد، روش ساده‌ SGD برای به‌روزرسانی وزن، گرادیان فعلی ∂L/∂w را بر عاملی به نام نرخ یادگیری () تقسیم می‌کند.

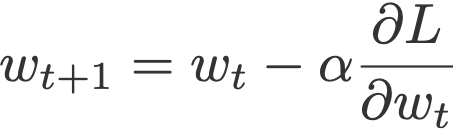
• ممنتوم

روش ممنتوم ( پلیاکPolyak ، ۱۹۶۴) برای به‌روزرسانی وزن تنها وابسته به گرادیان فعلی وابسته نیست، بلکه از مؤلفه‌ای به نام ممنتوم (m) که جمع گرادیان‌هاست نیز استفاده می‌کند. ممنتوم در واقع میانگین متحرک نمایی گرادیان‌های فعلی و گذشته (تا زمان t) است. در ادامه مشاهده خواهید کرد که بیشتر بهینه‌سازها برای به‌روزرسانی گرادیان از ممنتوم استفاده می‌کنند.

در این فرمول،

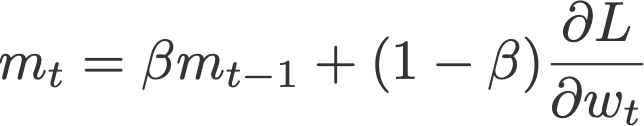
و به m مقدار صفر داده می‌شود.

مقدار پیش‌فرض معمول:

β = ۰.۹

ریشه‌ ممنتوم:

خیلی از مقالات روش ممنتوم را به نینج کیانNing Qian (۱۹۹۹) منتسب می‌کنند؛ اما مقاله‌ ساتسکور و دستیاران روش ممنتوم قدیمی را مربوط به کار پلیاک (۱۹۶۴) می‌داند.

• AdaGrad

روش گرادیان انطباقیAdaptive Gradient یا AdaGrad ( دوچی و دستیارانDuchi et al ، ۲۰۱۱) بر اساس مؤلفه‌ «نرخ یادگیری» عمل می‌کند؛ در این روش، نرخ یادگیری بر جذر v (جمع تراکمی مجذورات گرادیان‌های گذشته و فعلی تا زمان t) تقسیم می‌شود. توجه داشته باشید که در روش SGD، گرادیان ثابت و بدون تغییر باقی می‌ماند.

در این فرمول:

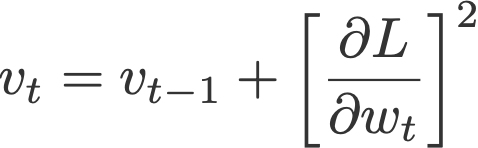
و به v مقدار صفر داده می‌شود.

بهε  که به مخرج اضافه شده است، توجه کنید. Keras این مؤلفه را fuzz factor می‌خواند؛ این عامل یک مقدار نقطه‌ای شناورA floating point value است که اطمینان حاصل می‌کند مخرج کسر هیچ‌گاه صفر نباشد.

مقادیر پیش‌فرض (برگرفته از Keras):

• α = ۰.۰۱
• ε = ۱۰⁻⁷
• RMSprop

RMSprop یا انتشار ریشه‌ میانگین مجذوراتRoot mean square propagation ( هینتون و دستیارانHinton et al ، ۲۰۱۲) یک نرخ یادگیری انطباقی دیگر است که برای ارتقای روش AdaGrad معرفی شده است. در این روش، به جای محاسبه‌ جمع تراکمی مجذورات گرادیان‌ها (مثل روش AdaGrad) از میانگین متحرک نمایی این گرادیان‌ها استفاده می‌شود. این روش نیز همچون روش ممنتوم در بیشتر بهینه‌سازها کاربرد دارد.

در این معادله،

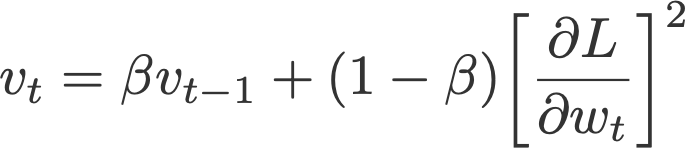
و به v مقدار صفر داده می‌شود.

مقادیر پیش‌فرض معمول (برگرفته از Keras):

• α = ۰.۰۰۱
• β = ۰.۹ (recommended by the authors of the paper)
• ε = ۱۰⁻⁶
• Adadelta

روش Adadelta ( زیلرZeiler ، ۲۰۱۲) نیز بر نرخ یادگیری تمرکز دارد و همچون روش RMSprop نسخه‌ ارتقایافته‌ روش AdaGrad محسوب می‌شود. نام این روش احتمالاً مخفف adaptive delta یا دلتای انطباقی است؛ دلتا نشان‌دهنده‌ تفاوت بین وزن فعلی و وزن به‌روزرسانی شده است.

تفاوت بین روش Adadelta و RMSprop این است که Adadelta پارامتر نرخ یادگیری را کاملاً کنار گذاشته و به جای آن از D ( میانگین متحرک نمایی مجذور دلتاهاExponential moving average of squared deltas ) استفاده می‌کند.

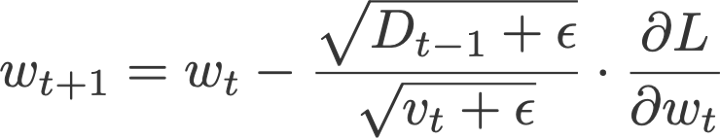
در این فرمول،

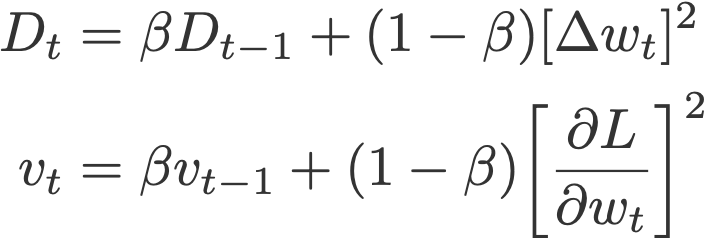
به D و v نیز مقدار صفر داده می‌شود.

مقادیر پیش‌فرض (برگرفته از Keras):

• β = ۰.۹۵
• ε = ۱۰⁻⁶
• گرادیان شتاب‌یافته‌ نستروفNestrov Accelerated Gradient (NAG)

پس از معرفی روش ممنتوم از سوی پولیاک، یک نسخه‌ مشابه ولی ارتقایافته از آن، با استفاده از گرادیان شتاب‌یافته‌ نستروف ( ساتسکور و دستیارانSutskever et al ، ۲۰۱۳)، پیاده‌سازی شد. این روش از m یعنی میانگین متحرک نمایی مؤلفه‌ای استفاده می‌کند که در این مقاله آن را گرادیان‌های پیش‌بینی‌شدهProjected gradients می‌نامیم.

در این فرمول،

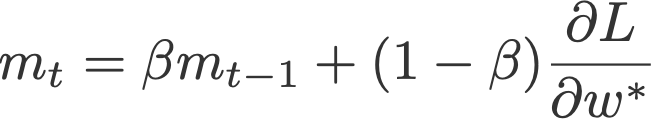
به m مقدار صفر داده می‌شود.

جمله‌ آخر این معادله نشان‌دهنده‌ گرادیان پیش‌بینی‌شده است. اگر با سرعت قبلی یک گام جلو برویم، به این مقدار می‌رسیم (معادله‌ پایین)؛ بدین معنی که در گام زمانی t، قبل از اجرای پس‌انتشار نهایی، باید یک انتشار به جلوی دیگر انجام دهیم. پس گام‌های اجرایی را می‌توان بدین ترتیب برشمرد:

1. به‌روزرسانی وزن کنونی w به وزن پیش‌بینی‌شده w*  بر اساس سرعت قبلی:

• اجرای انتشار روبه‌جلو با استفاده از وزن جدید؛
  • محاسبه‌ گرادیان پیش‌بینی‌شده‌ ∂L/∂w*؛
  • محاسبه‌ V و w .

مقدار پیش‌فرض معمول:

β = ۰.۹

ریشه‌ روش NAG

مقاله‌ اصلی گردایان شتاب‌یافته‌ نستروفNestrov Accelerated Gradient Paper (نستروف، ۱۹۸۳) درباره‌ گرادیان کاهشی تصادفی نیست و صراحتاً از معادله‌ گرادیان کاهشی استفاده نمی‌کند. به همین دلیل شاید بتوان مقاله‌ ساتسکور و دستیاران (۲۰۱۳) را منبع موثق‌تری برای این روش در نظر گرفت؛ این مقاله کاربرد NAG را در گرادیان کاهشی تصادفی توضیح می‌دهد.

• Adam

تخمین انطباقی گشتاورAdaptive moment estimation یا Adam ( کینگمن و باKingman and Ba ، ۲۰۱۴) را می‌توان ترکیبی از روش ممنتوم و RMSprop دانست. این روش بر این اساس عمل می‌کند:

1. مؤلفه‌ گرادیان: استفاده از m که میانگین متحرک نماییExponential moving average گرادیان‌هاست، همچون روش ممنتوم؛
2. مؤلفه‌ نرخ یادگیریLearning rate component : با تقسیم نرخ یادگیری α بر جذر v (میانگین نمایی متحرک مجذور گرادیان‌ها)، همچون روش RMSprop.

در این معادله،

این فرمول‌ها برای اصلاح سوگیری‌هاBias corrections به کار می‌روند و،

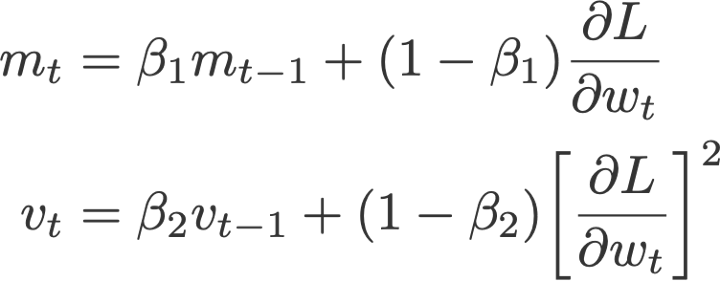
مقدار m و v صفر تعریف می‌شود.

مقادیر پیش‌فرض پیشنهادی:

• α = ۰.۰۰۱
• β₁ = ۰.۹
• β₂ = ۰.۹۹۹
• ε = ۱۰⁻⁸
• AdaMax

نویسندگان مقاله‌ بهینه‌ساز Adam (کینگمن و باو) با استفاده از نرم‌های بی‌نهایتInfinity norms (max)، روش Adamax (2015) را معرفی می‌کنند. m میانگین متحرک نمایی گرادیان‌ها و v میانگین متحرک نمایی p-norm  گذشته از گرادیان‌هاست که به تابع بیشینه‌ تقریب (همگرا) داده می‌شود (معادله‌ زیر). برای مشاهده‌ اثبات همگرایی به خود مقاله مراجعه نمایید.

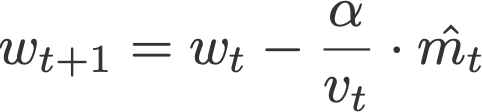
در این معادله،

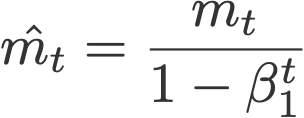
برای اصلاح سوگیری m استفاده می‌شود و

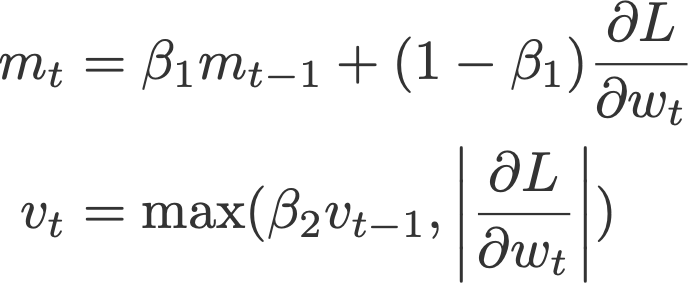
به m و v مقدار صفر داده می‌شود.

مقادیر پیش‌فرض پیشنهادی:

• α = ۰.۰۰۲
• β₁ = ۰.۹
• β₂ = ۰.۹۹۹
• Nadam

روش Nadam ( دوزاتDozat ، ۲۰۱۵) حاصل ترکیب بهینه‌سازهای Nesterov و Adam است؛ اما در این روش، مؤلفه‌ نستروف (نسبت به کاربرد خود در روش Nesterov) اصلاح و کارآمدتر شده است.

ابتدا به این نکته توجه کنید که معادله‌ بهینه‌ساز Adam را می‌توان بدین شکل هم نوشت:

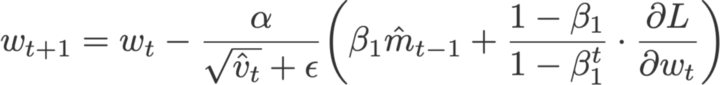
روش Nadam برای این‌که گرادیان را به اندازه‌ یک گام زمانی به‌روزرسانی کند، از بهینه‌ساز نستروف استفاده کرده و بدین منظور  در معادله‌ بالا را با  کنونی جایگزین می‌نماید:

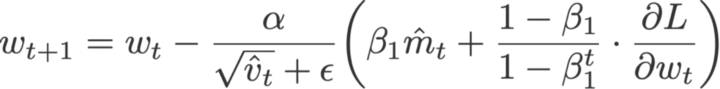
در این معادله،

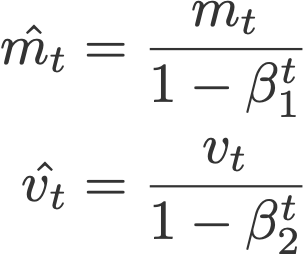
و

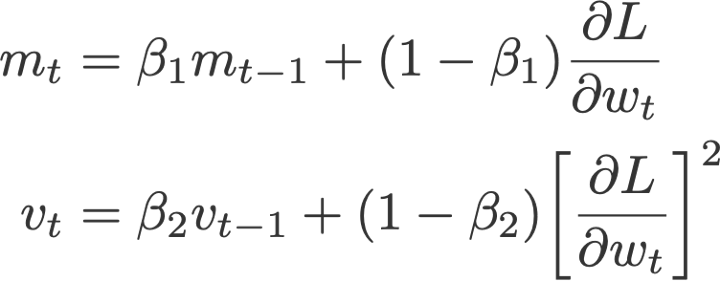
به m و v مقدار صفر داده می‌شود.

مقادیر پیش‌فرض (برگرفته از Keras):

• α = ۰.۰۰۲
• β₁ = ۰.۹
• β₂ = ۰.۹۹۹
• ε = ۱۰⁻⁷
• AMSGrad

AMSGrad ( ردی و دستیارانRedid et al ، ۲۰۱۸) نسخه‌ای دیگر از روش Adam است. این روش مجدداً از مؤلفه‌ نرخ یادگیری تطابقی (که در روش Adam مطرح شد) استفاده کرده و آن را  به‌نحوی تغییر می‌دهد که مطمئن شود v کنونی از v قبلی همواره بزرگ‌تر خواهد بود.

در این معادله،

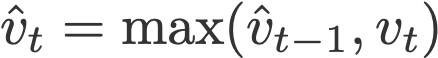
و

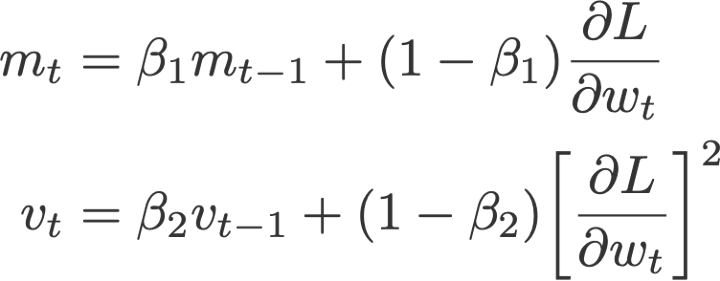
به m و v نیز مقدار صفر داده می‌شود.

مقادیر پیش‌فرض (برگرفته از Keras):

• α = ۰.۰۰۱
• β₁ = ۰.۹
• β₂ = ۰.۹۹۹
• ε = ۱۰⁻⁷

ضمیمه‌ ۱: چیت‌شیت

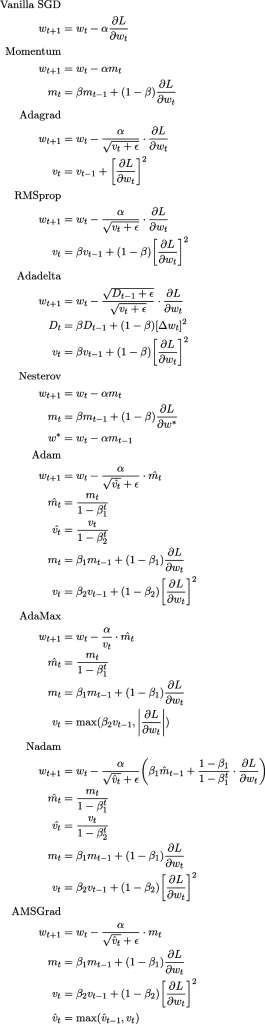
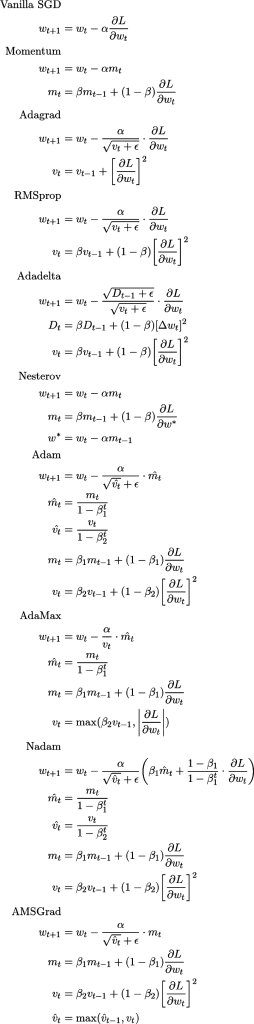
توضیح این قسمت را می‌توانید در این لینک مشاهده کنید؛ این تصویر با استفاده از QuickLaTeX تولید شده است.

ضمیمه‌ ۲: اطلاعات بیشتر

چرا بهینه‌سازهای گرادیان کاهشی از میانگین متحرک نمایی برای مؤلفه‌ گرادیان و از جذر میانگین برای مؤلفه‌ نرخ یادگیری استفاده می‌کنند؟ در این قسمت به این سؤال پاسخ خواهیم داد.

دلیل استفاده از میانگین متحرک‌نمایی گرادیان‌ها

همان‌طور که می‌دانید، هدف اصلی به‌روزرسانی وزن‌هاست و بدین منظور باید از مقادیر و مؤلفه‌هایی استفاده شود. تنها مقداری که قابل‌دسترس است، مقدار گرادیان فعلی است، پس برای به‌روزرسانی وزن باید از همین مقدار استفاده کنیم.

اما از آنجایی که می‌خواهیم به‌روزرسانی‌ها به‌خوبی انجام گیرند، استفاده از مقدار گرادیان فعلی به‌تنهایی کافی نخواهد بود. به همین دلیل با جمع گرادیان‌های قبلی و فعلی، از اطلاعات قبلی گرادیان‌ها نیز استفاده می‌کنیم.

یک راه برای جمع گرادیان‌ها محاسبه‌ میانگین سادهSimple average آن‌هاست؛ اما این کار به‌معنی یکسان در نظر گرفتن وزن همه‌ گرادیان‌هاست (در حالی ‌که از صحت این قضیه مطمئن نیستیم).

به همین دلیل، میانگین متحرک نمایی را محاسبه می‌کنیم و بدین طریق به مقادیر گرادیان‌های قبلی وزن (اهمیت) بیشتری می‌دهیم. با اختصاص وزن کمتر به گرادیان‌های کنونی، اطمینان حاصل می‌کنیم که فرایند به‌روزرسانی وزن‌ها به گرادیان‌های فعلی حساس نخواهد بود.

دلیل تقسیم نرخ یادگیری بر جذر میانگین‌نمایی مجذور گرادیان‌ها

هدف از به‌کارگیری نرخ یادگیری، هوشمندتر کردن بهینه‌سازهاست؛ به همین منظور، نرخ یادگیری را بر جذر میانگین مجذورات چندین گرادیان تقسیم می‌کنیم. اینجا چند سؤال مطرح می‌شود:

1. چرا چندین گرادیان؟
   1. چرا تقسیم؟
   1. چرا جذر میانگین متحرک نمایی مجذورات گرادیان‌ها؟

پاسخ به سؤال اول در قسمت قبل توضیح داده شد: می‌خواهیم علاوه بر مقادیر گرادیان‌های فعلی، از اطلاعات گرادیان‌های قبلی هم استفاده کنیم.

برای پاسخ به سؤال دوم، ابتدا یک موقعیت ساده را مجسم کنید که در آن میانگین گرادیان‌ها طی چند دور اخیر، ۰۱/۰ بوده است. این مقدار نزدیک ۰ است، بدین معنی که روی سطح تقریباً صافی (در نمای سه‌بُعدی تابع زیان) قرار داشته‌ایم. پس با سطح اطمینان خوبی می‌توانیم در این منطقه حرکت کنیم؛ اما می‌خواهیم به سرعت از این منطقه خارج شده و به دنبال یک شیب رو به پایین بگردیم که می‌تواند ما را به مقدار کمینه‌ کلیGlobal minima برساند (ممکن است به مقالاتی بربخورید که معتقدند این امر تأثیر شتاب‌بخشی و تسریع‌کنندگی دارد). به همین دلیل در شرایطی که مقدار گرادیان‌ها کم است، باید مؤلفه‌ نرخ یادگیری را افزایش دهیم (یعنی سرعت آموزش را بیشتر کنیم). پس می‌توان گفت یک رابطه‌ معکوس وجود دارد که برای نشان دادن آن، نرخ یادگیری ثابت α  را بر میانگین مقدار گرادیان‌ها تقسیم می‌کنیم. با تقسیم این نرخ یادگیری انطباق‌یافته (که اکنون مقدار بزرگی دارد) بر مؤلفه‌ گرادیان، وزن‌ها به‌خوبی به‌روزرسانی می‌شوند (مثبت یا منفی).

عکس این نکته هم صدق می‌کند: فرض کنید میانگین گرادیان‌ها خیلی بزرگ است (تقریباً ۲.۷)، بدین معنی که روی شیب‌های تندی قرار داریم. برای اینکه جانب احتیاط را حفظ کنیم، باید قدم‌های کوچک بر‌داریم؛ این کار هم با عملیات تقسیمی که توضیح داده شد، امکان‌پذیر خواهد بود.

دلیل استفاده از میانگین متحرک نمایی را در قسمت قبلی توضیح دادیم. استفاده از مجذور گرادیان‌ها نیز دلیل واضحی دارد: چون وقتی با مؤلفه‌ نرخ یادگیری سروکار داریم، بزرگی و مقدار آن برای ما مهم است. بنابراین یکی از بدیهی‌ترین راه‌حل‌ها این است که جذر این پارامتر را به کار ببریم. البته آنچه گفته شد، صرفاً یک توضیح ساده و مقدماتی بود و اصل این عملیات، ریشه در ریاضیات دارد.

ضمیمه‌ ۳: مقایسه‌ زمان‌بندهای نرخ یادگیری با بهینه‌سازهای گرادیان کاهشی تصادفی

شاید از خود بپرسید تفاوت بین زمان‌بندهای نرخ یادگیری و بهینه‌سازهای گرادیان‌ کاهشی تصادفی چیست؟ تفاوت اصلی بین این دو را می‌توان در این دانست که بهینه‌سازهای گرادیان کاهشی تصادفی از مؤلفه‌ نرخ یادگیری (با تقسیم نرخ یادگیری بر تابع گرادیان‌ها) استفاده می‌کنند، اما زمان‌بندهای نرخ یادگیری، نرخ یادگیری را در یک عامل (تابعی از گام زمانی و یا یک مقدار ثابت) ضرب می‌کنند.