متدهایی برای ارزیابی عملکرد مدل طبقه بندی

در این نوشتار قصد داریم تعدادی از متدهای ارزیابی عملکرد مدل طبقه بندی را به شما معرفی کنیم:

• Cross Validation مدل
• ماتریس در هم ریختگی(Confusion Matrix)
• منحنی ROC
• امتیازCohen’s κ

import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import warnings

warnings.filterwarnings('ignore')

در گام اول، دیتاست‌های ساده‌ای ایجاد می‌کنیم که سه ستون ویژگی دارند و با برچسب‌هایی باینری (دودویی) برچسب‌گذاری شده‌اند:

from sklearn.model_selection import train_test_split

# Creating the dataset
N = 1000 # number of samples
data = {'A': np.random.normal(100, 8, N),
        'B': np.random.normal(60, 5, N),
        'C': np.random.choice([1, 2, 3], size=N, p=[0.2, 0.3, 0.5])}
df = pd.DataFrame(data=data)

# Labeling 
def get_label(A, B, C):
    if A < 95:
        return 1
    elif C == 1:
        return 1
    elif B > 68 or B < 52:
        return 1
    return 0

df['label'] = df.apply(lambda row: 
get_label(row['A'],row['B'],row['C']),axis=1)

# Dividing to train and test set
X = np.asarray(df[['A', 'B', 'C']])
y = np.asarray(df['label'])
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)

برای نمایش نتایج از یک رگرسیون خطی ساده استفاده می‌کنیم:

from sklearn import linear_model
from sklearn.model_selection import cross_val_score

clf = linear_model.LogisticRegression()
clf.fit(X_train, y_train)

print(">> Score of the classifier on the train set is: 
", round(clf.score(X_test, y_test),2))

>> Score of the classifier on the train set is:  0.74

Cross Validation

یکی از متدهای ارزیابی عملکرد مدل طبقه بندی متد Cross Validation است که بسیار ساده است: مقداری برای k انتخاب می‌کنیم، معمولاً k=5 یا k=10 ( در کتابخانه sklearn، 5 مقدار پیش‌فرض است). سپس داده‌ها را به k بخش مساوی تقسیم می‌کنیم و مدل را بر روی k-1 تا از بخش‌های مذکور آموزش می‌دهیم و عملکرد آن را بر روی بخش‌های باقیمانده ارزیابی و بررسی می‌کنیم. این عملیات را k دفعه انجام می‌دهیم و میانگین نمرات را محاسبه می‌کنیم، مقدار میانگین برابر است با امتیاز CV.

مزایا: متدCV نحوه عملکرد مدل‌تان را به شما نشان می‌دهد. این متد بسیار قدرتمند است (بر خلاف متدهایی که در آن‌ها دیتاست را به دو بخش آموزشی و آزمایشی تقسیم می‌کنیم). با استفاده از این متد می‌توانیم اَبَرپارامترها را به صورت دقیق تنظیم کنیم: به بیان دیگر، اگر یک پارامتر داشته باشیم، با استفاده از امتیاز CV می‌توانیم مقدار آن را بهینه‌سازی کنیم.

امتیاز CV مثالی که ذکر کردیم بدین شکل خواهد بود:

scores = cross_val_score(clf, X_train, y_train, cv=10)
print('>> Mean CV score is: ', round(np.mean(scores),3))
pltt = sns.distplot(pd.Series(scores,name='CV scores 
distribution'), color='r')

>> Mean CV score is:  0.729

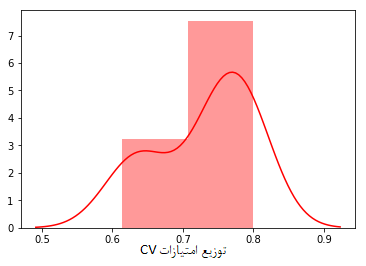
علاوه بر این، به کمک مقادیرِ امتیازات CV می‌توانیم فاصله اطمینان را به دست بیاوریم و در این فاصله می‌توانیم امتیاز واقعی را با احتمال بالایی پیدا کنیم.

ماتریس در هم ریختگی(Confusion Matrix)

ماتریس در هم‌ ریختگی نسبتاً ساده است. هدف از استفاده از این ماتریس این است که مثبت صحیح (TP)، منفی‌های صحیح (TN)، مثبت‌های کاذب (FP) و منفی‌های کاذب (FN) را نشان دهیم. فرض کنید تعدادی برچسب داریم؛ با استفاده از این ماتریس می‌توانیم تعداد نقطه‌ها داده‌هایی که با برچسب i برچسب‌گذاری شده‌اند اما در کلاس j طبقه‌بندی شده‌اند را نشان می‌دهیم. این عدد به صورت (i.j) تعریف می‌شود و ورودی ماتریس در هم ریختگی خواهد بود.

from sklearn.metrics import confusion_matrix
C = confusion_matrix(clf.predict(X_test),y_test)
df_cm = pd.DataFrame(C, range(2),range(2))
sns.set(font_scale=1.4)
pltt = sns.heatmap(df_cm, annot=True,annot_kws={"size":
16}, cmap="YlGnBu",  fmt='g')

منحنی ROC

در این قسمت، نگاه دقیق‌تری به ماتریس در هم ریختگی خواهیم داشت. پیش از این، مفاهیم مثبت‌های کاذب (TP) و مثبت‌های کاذب (FP) را توضیح دادیم. طبیعتاً اگر FP برابر با 1  باشد، TP هم برابر با 1 خواهد بود. به طور کلی، اگر مقدار TP و FP با هم برابر باشد، پیش‌بینی‌مان به خوبی یک حدس تصادفی خواهد بود.

منحنی ROC نموداری است که در آن TP نسبت به (به عنوان تابعی از) FP سنجیده می‌شود. لذا، با توجه به آنچه گفتیم، منحنی ROC در قسمت بالای خط y=x قرار خواهد گرفت.

منحنی ROC بر مبنای احتمالاتی ترسیم می‌شود که کلاسیفایرها به هر یک از نقاط تخصیص داده‌اند؛ برای هر نقطه‌داده xi که برچسب li∈{0,1} برای آن پیش‌بینی شده، احتمال pi∈[0,1]  را به شکل yi=li خواهیم داشت.

from sklearn.metrics import confusion_matrix, 
accuracy_score, roc_auc_score, roc_curve
pltt = plot_ROC(y_train, clf.predict_proba(X_train)
[:,1], y_test, clf.predict_proba(X_test)[:,1])

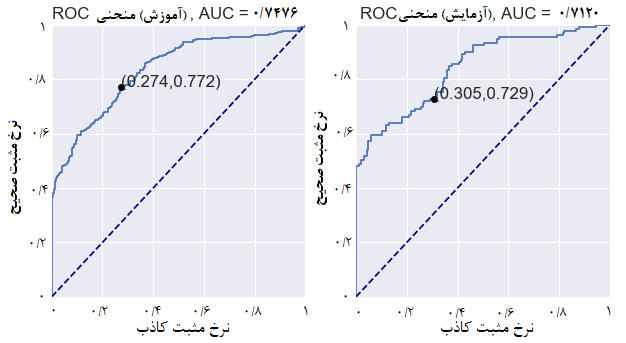
در منحنی ROC به چند نکته مهم باید توجه داشته باشید:

• مساحت زیرمنحنی (AUC) معیار مهمی برای سنجش کیفیت کلاسیفایر است. AUC یک حدس تصادفی برابر با AUC=∫xdx=1/2 است، بنابراین، انتظار داریم امتیاز یک کلاسیفایر مشخص score >1/2 باشد. معمولاً از AUC منحنی ROC در یادگیری ماشین استفاده می‌شود. در این حالت می‌توانیم بگوییم که مثبت‌های تصادفی (به لحاظ احتمال مدل) بیشتر از منفی‌های تصادفی بوده‌اند.
• نقاطی که بر روی نمودار مشخص شده‌اند، نرخ‌های TP و FP هستند.
• اگر منحنی ROC زیر خط y=x باشد، به این معناست که اگر نتایج کلاسیفایر را معکوس کنیم، یک کلاسیفایر آموزنده به دست خواهیم آورد. با اجرای کد زیر می‌توانید منحنی ROC را ترسیم کنید:

def plot_ROC(y_train_true, y_train_prob, y_test_true, 
y_test_prob):
    '''
    a funciton to plot the ROC curve for train labels and test labels.
    Use the best threshold found in train set to classify items in test set.
    '''
    fpr_train, tpr_train, thresholds_train = roc_curve(y_train_true, y_train_prob, pos_label =True)
    sum_sensitivity_specificity_train = tpr_train + (1-fpr_train)
    best_threshold_id_train = np.argmax(sum_sensitivity_specificity_train)
    best_threshold = thresholds_train[best_threshold_id_train]
    best_fpr_train = fpr_train[best_threshold_id_train]
    best_tpr_train = tpr_train[best_threshold_id_train]
    y_train = y_train_prob > best_threshold

    cm_train = confusion_matrix(y_train_true, y_train)
    acc_train = accuracy_score(y_train_true, y_train)
    auc_train = roc_auc_score(y_train_true, y_train)

    fig = plt.figure(figsize=(10,5))
    ax = fig.add_subplot(121)
    curve1 = ax.plot(fpr_train, tpr_train)
    curve2 = ax.plot([0, 1], [0, 1], color='navy', linestyle='--')
    dot = ax.plot(best_fpr_train, best_tpr_train, marker='o', color='black')
    ax.text(best_fpr_train, best_tpr_train, s = '(%.3f,%.3f)' %(best_fpr_train, best_tpr_train))
    plt.xlim([0.0, 1.0])
    plt.ylim([0.0, 1.0])
    plt.xlabel('False Positive Rate')
    plt.ylabel('True Positive Rate')
    plt.title('ROC curve (Train), AUC = %.4f'%auc_train)

    fpr_test, tpr_test, thresholds_test = roc_curve(y_test_true, y_test_prob, pos_label =True)

    y_test = y_test_prob > best_threshold

    cm_test = confusion_matrix(y_test_true, y_test)
    acc_test = accuracy_score(y_test_true, y_test)
    auc_test = roc_auc_score(y_test_true, y_test)

    tpr_score = float(cm_test[1][1])/(cm_test[1][1] + cm_test[1][0])
    fpr_score = float(cm_test[0][1])/(cm_test[0][0]+ cm_test[0][1])

    ax2 = fig.add_subplot(122)
    curve1 = ax2.plot(fpr_test, tpr_test)
    curve2 = ax2.plot([0, 1], [0, 1], color='navy', linestyle='--')
    dot = ax2.plot(fpr_score, tpr_score, marker='o', color='black')
    ax2.text(fpr_score, tpr_score, s = '(%.3f,%.3f)' %(fpr_score, tpr_score))
    plt.xlim([0.0, 1.0])
    plt.ylim([0.0, 1.0])
    plt.xlabel('False Positive Rate')
    plt.ylabel('True Positive Rate')
    plt.title('ROC curve (Test), AUC = %.4f'%auc_test)
    plt.savefig('ROC', dpi = 500)
    plt.show()

    return best_threshold

امتیاز Cohen’s κ

ضریب کاپای کوهن میزان توافق دو کلاسیفایر بر روی داده‌های یکسان را نشان می‌دهد. ضریب کاپا بدین شکل تعریف می‌شود: κ=1−(1−po)/(1−pe). در این معادله po نشان‌دهنده احتمال توافق و pe احتمال تصادفی توافق است.

به این مثال توجه کنید. در اینجا لازم است از یک کلاسیفایر دیگر هم استفاده کنیم:

from sklearn import svm

clf2 = svm.SVC()
clf2.fit(X_train, y_train)

print(">> Score of the classifier on the train set is: 
", round(clf2.score(X_test, y_test),2))

>> Score of the classifier on the train set is:  0.74

ضریب κ را  دیتاست آموزشی محاسبه می‌کنیم.

y = clf.predict(X_test)
y2 = clf2.predict(X_test)
n = len(y)

p_o = sum(y==y2)/n # observed agreement

p_e = sum(y)*sum(y2)/(n**2)+sum(1-y)*sum(1-y2)/(n**2) # random agreement: both 1 or both 0

kappa = 1-(1-p_o)/(1-p_e)

print(">> Cohen's Kappa score is: ", round(kappa,2))

>> Cohen's Kappa score is:  0.4

که توافق میان دو کلاسیفایر را نشان می‌دهد. κ=0 به این معناست که دو کلاسیفایر با هم توافق ندارند و κ<0 نیز عدم توافق میان دو کلاسیفایر را نشان می‌دهد.

نتیجه‌گیری

در این نوشتار که مربوط به ارزیابی عملکرد مدل طبقه بندی بود، به معرفی چندین معیار برای سنجش و مقایسه عملکرد یک مدل با مدل‌های دیگر پرداختیم. این معیارها در زمان استفاده از الگوریتم‌های ML و مقایسه عملکرد آن‌ها یا یکدیگر اهمیت زیادی دارند.