
آزمایش بیزی AB ــ قسمت اول: تبدیلها
در این مقاله، درباره محاسبات و نحوه پیادهسازی آزمایش بیزی AB در دنیای واقعی بحث میشود. فهرستی از مطالبی که در این متن توضیح داده میشود از این قرار است:
- مدلسازی و تجزیهوتحلیل معیارهای آزمایشی مبتنی بر تبدیل (معیارهای نرخی (Rate Metrics))
- مدلسازی و تجزیه و تحلیل معیارهای آزمایشی مبتنی بر درآمد
- محاسبه دوره آزمایش
- انتخاب پیشین مناسب
- اجرای آزمایش با چندین متغیر
بستر آزمایش
فرض کنید اخیراً در پیامرسانی روی صفحه پرفروشها تغییراتی ایجاد شده است و اکنون قرار است قبل از آنکه این تغییرات به شکل گستردهتری بین کاربران منتشر شود، در چارچوب AB آن را آزمایش کنیم. فرض میکنیم که تغییراتی که اعمال شده به نرخ تبدیل بسیار بهتری منجر خواهد شد.
مشابه با روشهای فراوانی (Frequentist Method)، میتوان هر تبدیل روی صفحه پرفروشها را با X به صورت متغیر تصادفی برنولی (Bernoulli random variable) با احتمال تبدیل ? مدل کرد:
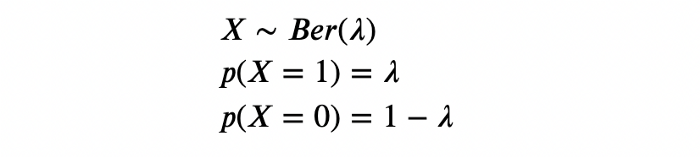
در شیوه فراوانی، ? مقدار ثابتی فرض میشد، اما در شیوه بیزی، این پارامتر یک متغیر تصادفی در نظر گرفته میشود که توزیع احتمالات خودش را دارد. گام اول، انتخاب برآوردی مناسب برای این توزیع با استفاده از دادههای گذشته است. به این توزیع، توزیع پیشین (Prior Distribution) ? گفته میشود.
سپس آستانه زیان تعیین میشود. آستانه زیان بیشترین مقدار زیان قابلانتظار است که در صورت خطا همچنان قابل قبول خواهد بود. روشهای آزمایشی بیزی، نیز مثل بسیاری از مدلهای آماری دیگر، مبتنی بر برآورد دادههای دنیای واقعی هستند. به همین دلیل، همیشه احتمال نتیجهگیری اشتباه از آزمایشها وجود دارد. آستانه زیان تضمین میکند، حتی در صورت نتیجهگیری اشتباه، نرخ تبدیل بیشتر از حد مجاز تعیینشده، افت نخواهد کرد.
سرانجام، نمونهها در قالب آزمایشی تصادفی توصیف میشوند و از آنها برای بهروزرسانی این توزیع احتمال استفاده میشود. بدین ترتیب، باورها راجع به مقدار ? در گروه کنترل و تیمار (Treatment) نیز اصلاح خواهد شد. از این توزیعهای پسین برای محاسبه احتمال برتری نسبت به کنترل (عدم تیمار) و زیان موردانتظار (در صورت انتخاب اشتباه تیمار) استفاده میشود.
پس، اولین گام برای انتخاب توزیع پیشین ? بررسی دادههایی است که اخیراً (طی چند هفته گذشته) درباره نرخ تبدیل جمعآوری شده است. در ادامه دیتاستی که از نمونههای پیشین تولیدشده آمده است که میتوان از آن برای این تمرین استفاده کرد.
import pandas as pd
prior_data = pd.read_csv('prior_data.csv')

از آنجایی که این دیتاست به شکل مصنوعی تولید شده است، از پیش قالب آن برای این تمرین ایدئال است، در دنیای واقعی، احتمالاً لازم است مقداری عملیات استخراج، تبدیل، بارگذاری (ETL) انجام شود تا دادهها به این قالب درآیند. توضیح این عملیات خارج از حوصله این نوشتار است.
همانطور که مشاهده میکنید اندازه نمونه ما 5268 نفر است. برای هر کاربر، قابل مشاهده است که آیا او به این صفحه راغب شده است یا خیر. این رویه با محاسبه نرخ تبدیل پیشین ادامه مییابد.
conversion_rate = prior_data['converted'].sum()/prior_data.shape[0]print(f'Prior Conversion Rate is {round(conversion_rate, 3)}')

انتخاب توزیع پیشین
نرخ تبدیلی که بر اساس دادههای پیشین به دست آمد حدود 30% است. حال میتوان از این مقدار برای انتخاب توزیع پیشین برای ? استفاده کرد. انتخاب توزیع پیشین، از جنبههای مهم شیوههای آزمایش بیزی است که درخور مقالهای جداگانه است. در هر صورت، با توجه به هدف این مقاله، از روشی تقریبی برای انتخاب پیشین استفاده شده است.
اینجا از توزیع بتا (Beta distribution) برای مدلسازی نرخ تبدیل استفاده شده است، زیرا توزیعی انعطافپذیر در بازه است و علاوهبراین، یک پیشین مزدوج (Conjugate prior) مناسب به شمار میرود. این توزیع، محاسبات را در کار با توزیعهای پسین با دادههای آزمایشی آسانتر میکند.
هنگام انتخاب یک توزیع پیشین برای تبدیل، بهترین کار این است که یک پیشین ضعیفتر از چیزی که دادههای پیشین نشان میدهند، انتخاب کنیم. انتخاب یک پیشین زیادی قوی ممکن است باعث شود توزیعهای پسین غلط باشند و در نتیجه محاسبات و نتیجهگیریهای آن نادرست از کار در بیاید.
با توجه به این نکته، پیشینهای بالقوه با قوههای مختلف را در ادامه بررسی میکنیم:
import numpy as np
from scipy.stats import beta
import matplotlib.pyplot as pltfig, ax = plt.subplots(1, 1)x = np.linspace(0,1,1000)beta_weak = beta(round(conversion_rate, 1)*10 + 1, 10 + 1 - round(conversion_rate, 1)*10)beta_mid = beta(round(conversion_rate, 1)*50 + 1, 50 + 1 - round(conversion_rate, 1)*50)beta_strong = beta(round(conversion_rate, 2)*100 + 1, 100 + 1 - round(conversion_rate, 2)*100)ax.plot(x, beta_weak.pdf(x), label=f'weak Beta({int(round(conversion_rate, 1)*10) + 1}, {10 + 1 - int(round(conversion_rate, 1)*10)})')ax.plot(x, beta_mid.pdf(x), label=f'mid Beta({int(round(conversion_rate, 1)*50) + 1}, {50 + 1 - int(round(conversion_rate, 1)*50)})')ax.plot(x, beta_strong.pdf(x), label=f'strong Beta({int(round(conversion_rate, 2)*100) + 1}, {100 + 1 - int(round(conversion_rate, 2)*100)})')ax.set_xlabel('Conversion Probability')
ax.set_ylabel('Density')
ax.set_title('Choice of Priors')
ax.legend()
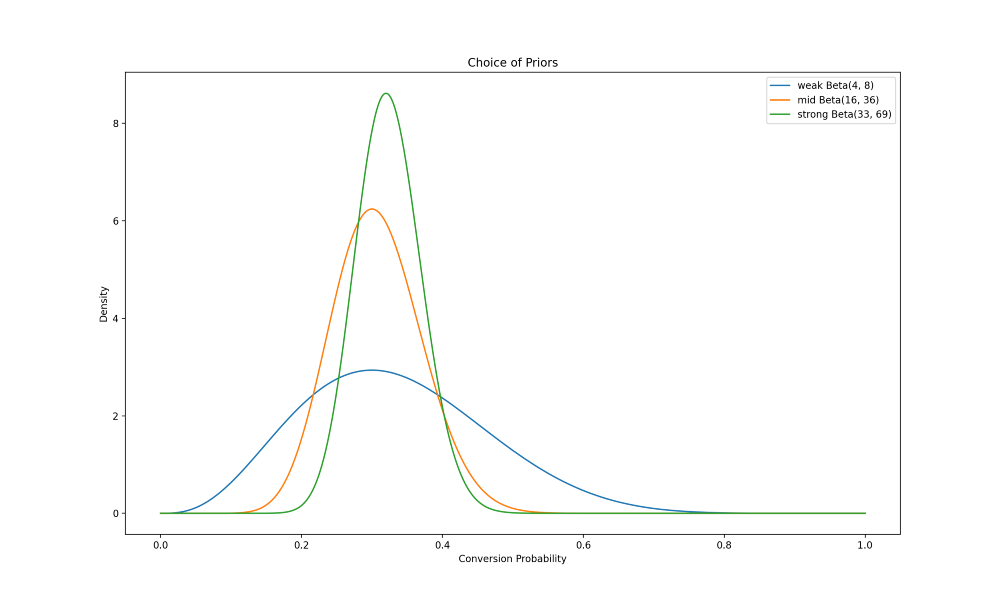
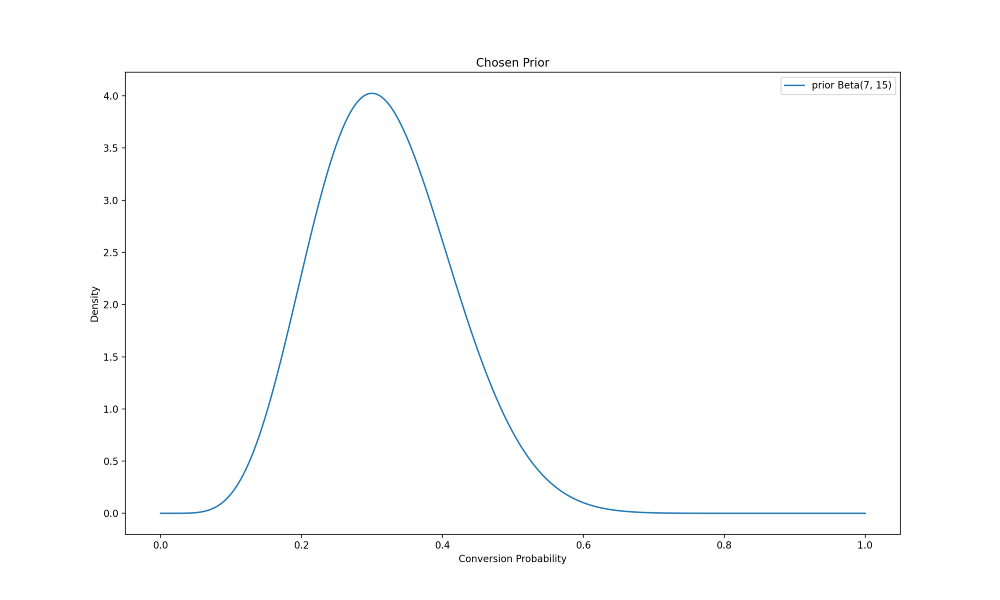
اینجا سه توزیع پیشین میبینیم که میانگین نرخ تبدیل آنها حدود 30% است (مثل دادههای اولیه). هر سه توزیع از توزیع واقعی دادههای اولیه بسیار ضعیفترند.
توزیع پیشین انتخابی چیزی بین ضعیفترین توزیع پیشین و توزیع پیشین میانی در این نمودار است؛ یعنی، Beta(7,15).
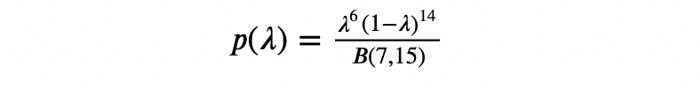
B(a,b) تابع بتا است که به این صورت تعریف میشود:
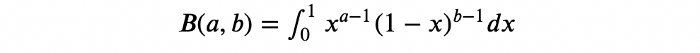
خاصیت تابع بتا این است که
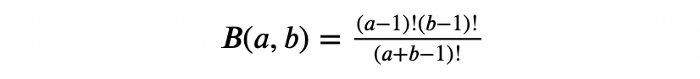
prior_alpha = round(conversion_rate, 1)*20 + 1
prior_beta = 20 + 1 - round(conversion_rate, 1)*20prior = beta(prior_alpha, prior_beta)fig, ax = plt.subplots(1, 1)x = np.linspace(0,1,1000)ax.plot(x, prior.pdf(x), label=f'prior Beta({int(round(conversion_rate, 1)*20) + 1}, {20 + 1 - int(round(conversion_rate, 1)*20)})')
ax.set_xlabel('Conversion Probability')
ax.set_ylabel('Density')
ax.set_title('Chosen Prior')
ax.legend()
تعیین آستانه زیان
بعد از انتخاب توزیع پیشین، باید ? را، یا بالاترین زیان مورد انتظار که میتوان در صورت بروز اشتباه در انتخاب گونه پذیرفت، مشخص کرد. فرض کنید که این تبدیل برای ما مهم است و میخواهیم در انتخاب ? بسیار دقیق و سختگیر باشیم. نمیخواهیم زیان موردانتظار مربوطه بیش از 0.5% باشد، پس مقدار آن را قرار میدهیم.
حالا که توزیع پیشین و آستانه زیان مشخص شد، میتوان آزمایش را اجرا کرد و دادههای حاصل از آن را جمعآوری نمود.
نتایج آزمایش
فرض کنید چند هفته آزمایشها در حالت اجرا (Running) گذاشته شده است و اکنون میخواهیم بررسی کنیم که آیا میشود از آنها نتیجهای گرفت. برای این کار باید از دادههای آزمایش برای محاسبه توزیعهای پسین استفاده کرد. توزیعهای پسین در گامهای بعد برای محاسبه میزان احتمال بهبود متغیرها و مقدار زیان مورد انتظار (در صورت انتخاب اشتباه متغیرها) به کار میروند.
برای این تمرین یک نمونه دیتاست آزمایشی تولید شده است. در اینجا دیتاست بررسی و تجمیع شده و نرخهای تبدیل برای هر متغیر به دست میآید.
experiment_data = pd.read_csv('experiment_data.csv')print(experiment_data.head())
print(experiment_data.shape)

همانطور که میبینید، این دیتاست شبیه به دیتاست پیشین است، با این تفاوت که ستونی اضافه در آن هست. این ستون مشخص میکند چه گروهی به کاربر تخصیص داده شده و در نتیجه، او چه گونهای را دیده است. مجدداً اشاره کنیم که از آنجایی که این دیتاست به شکل مصنوعی تولید شده است، شکل ایدهآلی برای این آزمایش دارد و لازم نیست عملیات اضافی ETL روی آن انجام شود.
در اینجا فرآیند ادامه یافته است و دادهها تجمیع شدهاند:
results = experiment_data.groupby('group').agg({'userId': pd.Series.nunique, 'converted': sum})results.rename({'userId': 'sampleSize'}, axis=1, inplace=True)results['conversionRate'] = results['converted']/results['sampleSize']print(results)

از طریق بازبینی میشود گفت که نرخ تبدیل در اثر تیمار بهتر شده است، اما باید محاسبات بیشتری انجام شود تا باورهایمان از احتمال تبدیل مربوطه ?_? و ?_? در گونههای کنترل و تیمار بهروزرسانی شود.
اکنون، با استفاده از این دادههای آزمایشی، میتوان توزیعهای پسین مربوط به هر گونه را محاسبه کرد. اما قبل از انجام این کار، با مرور مبانی ریاضی ببینیم که این کار چگونه تنها با اطلاعاتی که در دست داریم ممکن است. با استفاده از قضیه [1] فرض کنید احتمال پیشین را داریم:
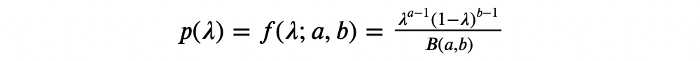
فرض کنید یک گونه برای n بازدیدکننده نمایش داده میشود و c نفر متقاعد میشوند، آنگاه توزیع احتمال پسین این گونه از طریق زیر به دست میآید:
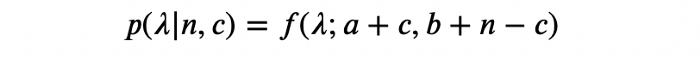
معادله بالا را میتوانیم با استفاده از قضیه بیز (Bayes theorem) اثبات کنیم:
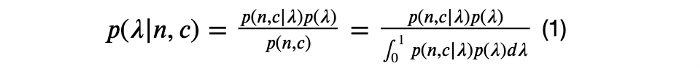
از آنجایی که هر تبدیل به صورت یک متغیر تصادفی برنولی (Bernoulli RV) با مقدار احتمال ? مدل شده است، با فرض داشتن ?، میتوان نتیجه نمایش یک گونه برای n بازدیدکننده را به صورت متغیر تصادفی دوجملهای (Binominal RV) مدلسازی کرد. پس
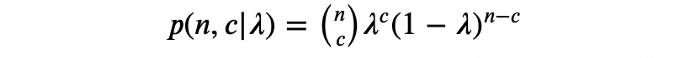
بدین ترتیب، با استفاده از تعریف توزیع پیشین:
![]()
حالا اگر تنها ضرایب در نظر گرفته شود:
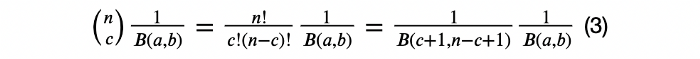
بر اساس تعریف تابع بتا میتوان نوشت:
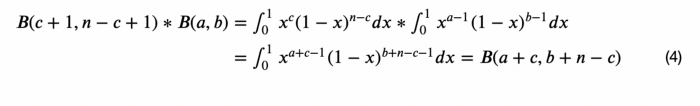
با جانشانی 3 و 4 در 2
![]()
و با جانشانی 5 در 1
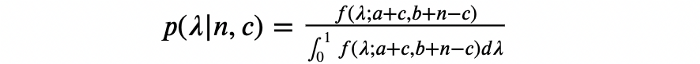
چون ?(?;?+?,?+?−?) توزیعی روی بازه [0,1] است، مخرج 1 خواهد بود و اثبات تمام میشود.
حالا با این پیشزمینه ریاضی، میتوان توزیعهای پسین را محاسبه کرد.
control = beta(prior_alpha + results.loc['control', 'converted'], prior_beta + results.loc['control', 'sampleSize'] - results.loc['control', 'converted'])treatment = beta(prior_alpha + results.loc['treatment', 'converted'], prior_beta + results.loc['treatment', 'sampleSize'] - results.loc['treatment', 'converted'])fig, ax = plt.subplots()x = np.linspace(0.26,0.42,1000)ax.plot(x, control.pdf(x), label='control')
ax.plot(x, treatment.pdf(x), label='treatment')
ax.set_xlabel('Conversion Probability')
ax.set_ylabel('Density')
ax.set_title('Experiment Posteriors')
ax.legend()
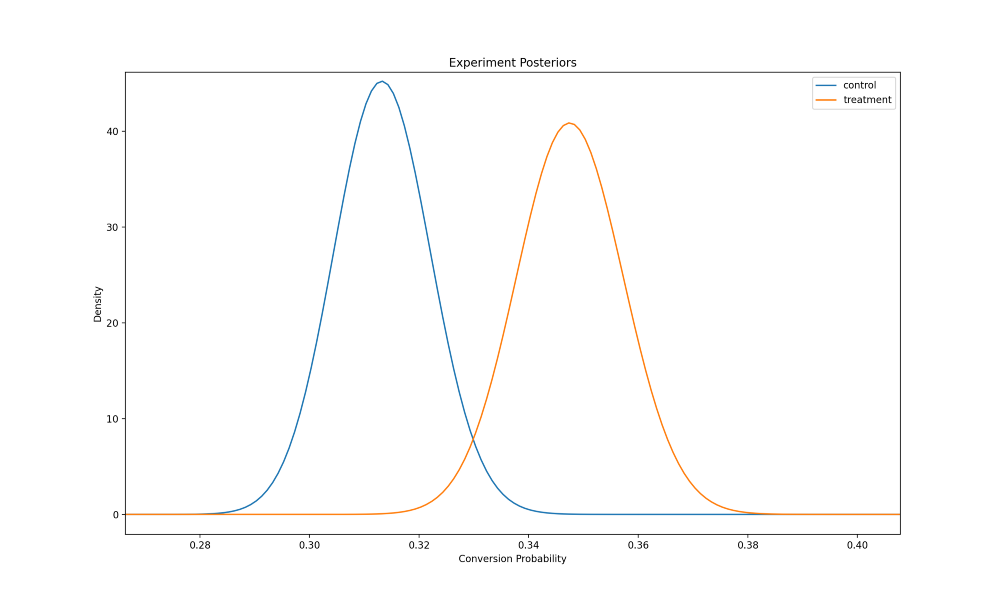
پس از محاسبه توزیعهای پسین، نوبت به محاسبه پسین توأم (Joint posterior) میرسد. از آنجایی که، آزمایشهای تصادفی مبتنی بر انتساب تصادفی (Random Assignment) یک کاربر به یک گونه ساخته میشوند، میتوان فرض کرد این دو توزیع مستقلاند. البته باید توجه داشته باشید که این مسئله همیشه صدق نمیکند. مثلاً، ممکن است موقعیتی پیش آید که تأثیرات شبکهای (Network Effects) روی نتایج نقش داشته باشند، در این حالت، باید این مسئله را در نظر گرفت. همچنین، این فرض به این بستگی دارد که روند انتساب تصادفی بهخوبی کار کند.
فرض کنید شیوه انتساب تصادفی در این آزمایش خوب کار میکند و هیچ تأثیر شبکهای وجود ندارد. با این فرض میتوان گفت:
![]()
از این رابطه برای محاسبه توزیع پسین توأم استفاده میکنیم:
import seaborn as snsjoint_dist_for_plot = []
for i in np.linspace(0.26,0.42,161):
for j in np.linspace(0.26,0.42,161):
joint_dist_for_plot.append([i, j, control.pdf(i)*treatment.pdf(j)])joint_dist_for_plot = pd.DataFrame(joint_dist_for_plot)joint_dist_for_plot.rename({0: 'control_cr', 1: 'treatment_cr', 2: 'joint_density'}, axis=1, inplace=True)tick_locations = range(0, 160, 10)
tick_labels = [round(0.26 + i*0.01, 2) for i in range(16)]heatmap_df = pd.pivot_table(joint_dist_for_plot, values='joint_density', index='treatment_cr', columns='control_cr')ax = sns.heatmap(heatmap_df)
ax.set_xticks(tick_locations)
ax.set_xticklabels(tick_labels)
ax.set_yticks(tick_locations)
ax.set_yticklabels(tick_labels)
ax.invert_yaxis()
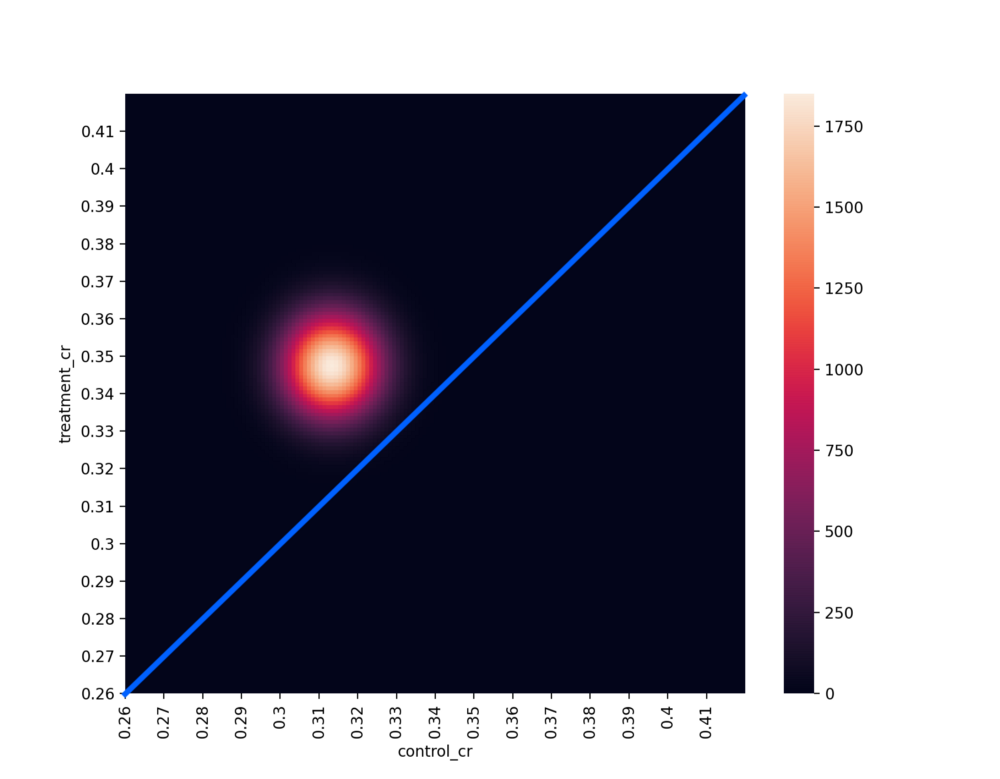
خط آبی در نمودار بالا خطی است که ?_?=?_? را بازنمایی میکند. از آنجایی که پسین توأم بالای این خط آبی است، میتوان گفت این نمودار به لحاظ بصری نشان میدهد که در واقع تیمار بهتر بوده است. اگر پسین توأم زیر این خط بود، میتوانستیم کاملاً مطمئن باشیم که کنترل بهتر است. اگر هر قسمتی از پسین توأم روی خط آبی قرار میگرفت، تردید بیشتری درباره اینکه کدام گونه بهتر بوده، وجود داشت.
برای کمیسازی آنچه گفته شد باید ?(?_?≥?_?) و ?[?](?) (زیان موردانتظار در صورت انتخاب تیمار اشتباه) را محاسبه کرد.
import decimal
decimal.getcontext().prec = 4control_simulation = np.random.beta(prior_alpha + results.loc['control', 'converted'], prior_beta + results.loc['control', 'sampleSize'] - results.loc['control', 'converted'], size=10000)treatment_simulation = np.random.beta(prior_alpha + results.loc['treatment', 'converted'], prior_beta + results.loc['treatment', 'sampleSize'] - results.loc['treatment', 'converted'], size=10000)treatment_won = [i <= j for i,j in zip(control_simulation, treatment_simulation)]chance_of_beating_control = np.mean(treatment_won)print(f'Chance of treatment beating control is {decimal.getcontext().create_decimal(chance_of_beating_control)}')
![]()
با توجه به شبیهسازیها میبینیم که ?(?_?≥?_?)=0.9718، بنابراین تیمار به احتمال 97% بهتر از کنترل است.
حالا که طبق محاسبات احتمال تیمار بهتر شده، باید ?[?](?) را محاسبه کرد. تابع زیان هر متغیر از رابطه زیر به دست میآید:
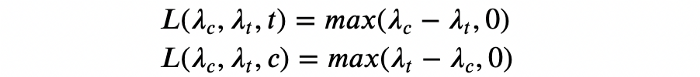
بدین ترتیب، تابع زیان موردانتظار برای هر گونه را میتوان از معادله زیر محاسبه کرد:
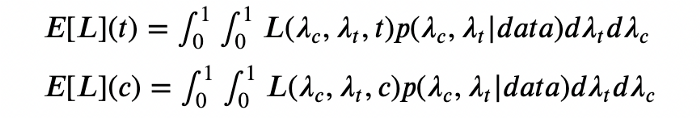
از این رابطه برای محاسبه زیان موردانتظار استفاده میکنیم:
decimal.getcontext().prec = 4loss_control = [max(j - i, 0) for i,j in zip(control_simulation, treatment_simulation)]loss_treatment = [max(i - j, 0) for i,j in zip(control_simulation, treatment_simulation)]all_loss_control = [int(i)*j for i,j in zip(treatment_won, loss_control)]all_loss_treatment = [(1 - int(i))*j for i,j in zip(treatment_won, loss_treatment)]expected_loss_control = np.mean(all_loss_control)
expected_loss_treatment = np.mean(all_loss_treatment)print(f'Expected loss of choosing control: {decimal.getcontext().create_decimal(expected_loss_control)}. Expected loss of choosing treatment: {decimal.getcontext().create_decimal(expected_loss_treatment)}')
با اجرای شبیهسازی میبینیم:
[?](?) = 0.0001369 < 0.0015 = ?
از آنجایی که زیان موردانتظار یک گونه، پایینتر از آستانهای است که در ابتدای آزمایش تعیین کردیم، میتوانیم بگوییم نتایج آزمایش معنادار بوده است. پس میتوانیم با اطمینان بالا نتیجهگیری کنیم که تیمار بهتر از کنترل است و زیان مورد انتظار در صورت انتخاب اشتباه تیمار از آنچه خود تعیین کردهایم بیشتر نخواهد بود. بدین ترتیب، قویاً توصیه میکنیم که گونه تیمار صفحه پرفروشها برای باقی کاربران نیز نمایش داده شود.





