
کدام توابع زیان و فعال سازی را باید در یادگیری عمیق به کار برد؟
در این نوشتار قصد داریم متناسب با هدف و مسئلهی موردنظر، توابع زیان و فعال سازی لایهی آخر شبکهی عصبی را معرفی کنیم.
فرض نویسنده بر این است که مخاطبان با توابع فعال سازی آشنایی دارند. برای آشنایی بیشتر با این حوزه میتوانید به این مقاله Deep Learning: Overview of Neurons and Activation Functions مراجعه کنید.

با چه مسئلهای روبرو هستید؟
همچون سایر مسائل یادگیری ماشینی، اینجا نیز هدف کار شیوه ارزیابی موفقیت را تعیین میکند.
- آیا میخواهید یک مقدار عددی پیشبینی کنید؟
مثال: پیشبینی قیمت مناسب برای یک محصول، یا پیشبینی میزان فروش در هرروز.
در این صورت، بخش رگرسیون: پیشبینی مقدار عددی را مطالعه نمایید.
- آیا میخواهید یک خروجی گسسته (ردهای) پیشبینی کنید؟
مثال: پیشبینی اشیای مشاهده شده در یک تصویر، یا پیشبینی موضوع یک مکالمه.
در این صورت باید تعداد ردههایی که در دست دارید و تعداد برچسبهای موردنظرتان را مشخص کنید.
اگر دادههای شما دودویی (چه به صورت ردهای و چه غیرردهای (مثل کلاهبرداری، تشخیص، احتمال خرید)) هستند به قسمت پیشبینی خروجی دودیی مراجعه نمایید.
در صورتی که چندین کلاس دارید (مثل اشیاء داخل یک تصویر، موضوعات ایمیلها، محصولات مناسب برای تبلیغات) و این کلاسها گسترده هستند (هر آیتم یک برچسب دارد) به قسمت پیشبینی برچسب واحد از چندین کلاس مراجعه کنید. اگر در دادههای خود چندین برچسب دارید، باید قسمت پیشبینی برچسبهای چندگانه از کلاسهای چندگانه را مطالعه کنید.
[irp posts=”21813″]رگرسیون: پیشبینی مقدار عددی
مثال: پیشبینی قیمت یک محصول
لایهی آخر شبکهی عصبی یک نورون داشته و مقداری که تولید میکند یک مقدار عددی پیوسته است.
برای قضاوت در مورد صحت پیشبینی، مقدار به دستآمده را با مقدار حقیقی (که خود نیز یک عدد پیوسته است) مقایسه میکنیم.

تابع فعال سازی نهایی
خطی: این تابع مقدار عددی موردنیاز را به دست میدهد.

یا
- ReLU: این تابع یک مقدار عددی بزرگتر از 0 تولید میکند.

تابع زیان
خطای مجذورات میانگین (MSE): این تابع، مجذورات میانگین تفاوتهای بین مقدار پیشبینی شده و مقدار حقیقی را پیدا میکند.

پیشبینی خروجی دودویی
مثال: پیشبینی جعل تراکنش
لایهی نهایی شبکهی عصبی یک نورون داشته و مقداری بین 0 و 1 تولید میکند که به صورت احتمال تفسیر میشود.
برای ارزیابی صحت پیشبینی، مقدار به دست آمده با مقدار واقعی مقایسه میشود. اگر دادهها در همان رده باشند، مقدار حقیقی 1 و در غیر این صورت 0 خواهد بود.

تابع فعال سازی نهایی
سیگموئید: این تابع مقداری بین 0 و 1 تولید میکند؛ این مقدار نشان میدهد مدل از قراردهی نمونه در ردهی مورد نظر چقدر اطمینان دارد.

تابع زیان
آنتروپی متقاطع دودویی: تابع آنتروپی متقاطع میزان تفاوت بین دو توزیع احتمال را تعیین میکند. مدل ما یک توزیع به شکل {p, 1-p} پیشبینی میکند زیرا یک توزیع دودویی داریم. از تابع آنتروپی متقاطع دودویی برای مقایسهی این توزیع با توزیع حقیقی{y, 1-y} استفاده میکنیم.
 [irp posts=”18831″]
[irp posts=”18831″]
پیشبینی یک برچسب واحد از چندین کلاس
مثال: پیشبینی موضوع یک سند
لایهی آخر شبکهی عصبی برای هر کلاس یک نورون دارد و مقداری بین 0 و 1 تولید میکند که میتواند به عنوان احتمال تفسیر شود. سپس یک توزیع احتمال از خروجی به دست میآید که مجموع آن 1 خواهد بود.
برای تشخیص صحت پیشبینی، هر خروجی با مقدار حقیقی خودش مقایسه میشود. مقادیر واقعی به صورت one-hot رمزگذاری شدهاند، بدین معنی که 1 در ستون مربوط به دستهی صحیح و 0 در ستون دیگر نمایان میشود.

تابع فعال سازی نهایی
سافتمکس: این تابع برای هر خروجی مقداری بین 0 تا 1 ارائه میدهد؛ حاصل جمع همهی این مقادیر با هم 1 است. بدین ترتیب در این مورد هم یک توزیع احتمال در دست داریم.

تابع زیان
آنتروپی متقاطع: تابع آنتروپی متقاطع میزان تفاوت بین دو توزیع احتمال را مشخص میکند. مدل ما یک توزیع مدل به صورت {p1, p2, p3} پیشبینی مینماید (که در آن p1+p2+p3 = 1). از تابع آنتروپی متقاطع برای مقایسهی این توزیع با توزیع حقیقی {y1, y2, y3} استفاده میکنیم.
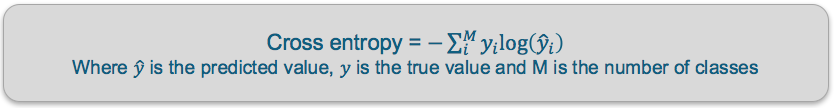
پیشبینی چندین برچسب از چندین کلاس
مثال: پیشبینی حضور حیوانات در یک تصویر
لایهی نهایی شبکهی عصبی برای هر کلاس یک نورون دارد و مقداری بین 0 تا 1 تولید میکند که به صورت احتمال در نظر گرفته میشود.
برای سنجش صحت پیشبینی، هر خروجی با مقدار حقیقی مربوط به خود مقایسه میشود. اگر در ستون مقادیر حقیقی، عدد 1 نمایش داده شود، یعنی دستهی مربوط به آن مقدار در ورودی حضور دارد؛ در غیر این صورت عدد 0 در آن ستون نمایش داده خواهد شد.

تابع فعال سازی نهایی
سیگموئید: این تابع مقداری بین 0 تا 1 به دست میدهد که نشان دهندهی میزان اطمینان مدل از حضور داده در آن کلاس میباشد.

تابع زیان
آنتروپی متقاطع دودویی: آنتروپی متقاطع تفاوت بین دو توزیع احتمال را مشخص میکند. مدل ما توزیع مدل به شکل {p, 1-p} (یک توزیع دودویی) را برای هر کدام از کلاسها پیشبینی مینماید. از آنتروپی متقاطع دودویی برای مقایسهی این توزیع با توزیع حقیقی {y, 1-y} در هر کلاس استفاده کرده و نتایج را با هم جمع میکنیم.
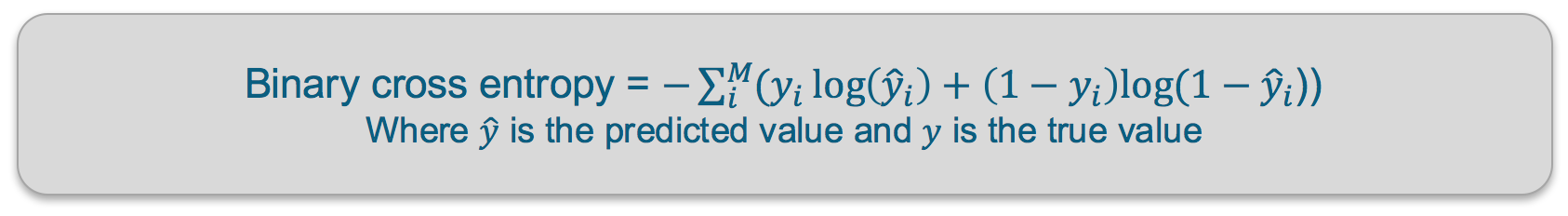
خلاصهی مطالب
جدول زیر اطلاعاتی را که تا اینجا بیان شد، جمعبندی میکند تا خوانندگان بتوانند تابع فعال سازی و تابع زیان لایهی نهایی را متناسب با مسئلهی خود و به سرعت پیدا کنند.







