مقدمه‌ای بر توابع پایه شعاعی: کرنل‌ها و شبکه‌های RBF

در این مقاله قصد داریم مقدمه‌ای بر تابع‌های پایه شعاعی را ارائه دهیم. در مقابل، مجموعه‌ای از داده‌های تک بُعدی را مشاهده می‌کنید. کاری که باید انجام دهید این است که راهی بیابید و این داده‌ها را به وسیله یک خط به دو کلاس جداگانه تقسیم کنید.

شاید در نگاه اول این کار غیرممکن به نظر برسد، اما فقط تا زمانی‌ اینگونه است که خودمان را به یک بُعد محدود کنیم.

در این بخش قصد داریم تابع موج‌دار  f(x) را به شما معرفی کنیم و سپس هر یک از مقادیر x را به خروجی مربوطه نگاشت کنیم. در نتیجه تعریف این تابع، تمامی نقاط آبی در قسمت فوقانی و تمامی نقاط قرمز در قسمت پایین و  در جای مناسب قرار خواهند گرفت. تنها کاری که لازم است انجام دهیم این است که یک خط افقی ترسیم کنیم و داده‌ها را به دو کلاس جداگانه تقسیم کنیم.

این راهکار کمی زیرکانه به نظر می رسد اما  با استفاده از توابع پایه شعاعی (RBF) می‌توانیم آن را تعمیم دهیم. با اینکه این توابع موارد کاربرد خاصی دارند اما نقاط آن‌ها فقط بر مبنای فاصله از مرکز تعریف می‌شوند. الگوی یادگیری میان تمامی متدهایی که از توابع RBF استفاده می‌کنند، یکسان است، اما با الگوی استاندارد ML تفاوت دارد و همین موضوع باعث قدرتمند شدن این توابع می‌شود.

برای مثال، منحنی زنگوله ای نمونه‌ای از RBF است، چراکه در این منحنی نقاط بر مبنای انحراف معیار از میانگین تعریف می‌شوند. بدین صورت می‌توانیم تابع RBF را تعریف کنیم:

توجه داشته باشید که double pipe (در این مورد) بدون در نظر گرفتن ابعاد x، نمایان‌گر «فاصله» است. برای مثال می‌تواند:

• مقدار مطلق در یک بُعد باشد: f(-3) = f(3) فاصله تا مبدأ (0) ،بدون در نظر گرفتن علامت، برابر با 3 خواهد بود.
• فاصله اقلیدسی در دو بُعد باشد: f([-3,4]) = f([3,-4]) . فاصله تا مبدأ ، بدون در نظر گرفتن موقعیت دقیق نقطه، برابر با 5 واحد خواهد بود.

این مورد همان «شعاعِ» توابع پایه شعاعی است. RBFها در اطراف مبدأ متقارن هستند.

مسئله‌ای که در قسمت بالا از آن صحبت کردیم – تقسیم نقاط با یک خط- با عنوان کرنل RBF شناخته می‌شود و در الگوریتم‌های Support Vector Machine (SVM) کاربرد دارد. هدف تکنیک «کَلَک کرنل» این است که نقاط را به فضایی با ابعاد بیشتر نگاشت کند و در فضای جدید با استفاده از متدهای خطی آن‌ها را جدا کند.

به این مثال ساده توجه کنید. فرض کنید فقط سه نقطه دارید و باید آن‌ها را از هم جدا کنید:

در این قسمت ، در مرکز هر یک از این نقاط یک توریع نرمال (یا یک تابع RBF دیگر) رسم می‌کنیم:

سپس می‌توانیم تمامی توابع RBF را برای نقطه‌داده‌های موجود در یک کلاس معکوس می‌کنیم:

در صورتی‌که تمامی مقادیر توابع RBF را به نقاط x اضافه کنیم، یک تابع میانجی global به شکل زیر به دست می‌آوریم:

تابع kernel trick موج‌دار (که آن را g(x) می‌نامیم) به دلیل ماهیت تابع RBF می‌تواند با هر نوع داده‌ای کار کند.

تابع RBF انتخابی ما، یعنی توزیع نرمال، در یکی از نواحی مرکزی چگالی بیشتری دارد و در نواحی دیگر چگالی کمتری دارد. به همین دلیل، زمانی‌که مقادیر x به موقعیت g(x)  نزدیک باشند، محاسبه مقدار آن همراه با نوسان خواهد بود و هرچه این فاصله افزایش پیدا کند، نوسان کمتر می‌شود. همین ویژگی باعث قدرتمند شدن توابع RBF می‌شود.

چنانچه تک تک نقاط اصلی در موقعیت x را به نقاط موجود در فضای دو بُعدی (x, g(x)) نگاشت کنیم، می‌توانیم داده‌ها را به سادگی و بدون اینکه نویز زیادی داشته باشند جدا کنیم. به دلیل همپوشانی توابع RBF نقاط اصلی بر طبق چگالی داده‌ها به نقاط جدید نگاشت می‌شوند.

در واقع، با استفاده از ترکیب خطی – ضرب و تقسیم- توابع RBF تقریباً می‌توانیم هر نوع تابعی را تخمین بزنیم.

تابعی (سیاه) که برای مدل‌سازی نقطه‌داده‌ها (بنفش) استفاده شده، شامل چندین تابع RBF است.

شبکه‌های پایه شعاعی، با اتکا بر همین مفهوم، «نورون‌های پایه شعاعی» را در یک شبکه دو لایه ساده به کار می‌گیرند:

بُردار ورودی یک ورودی n بُعدی است که عملیات طبقه‌بندی یا رگرسیون (فقط در نورون خروجی) در آن انجام می‌شود. یک کپی از بردار ورودی به نورون‌های شعاعی بعدی فرستاده می‌شود.

هر یک از نورون‌های RBF یک بُردار «مرکزی» را ذخیره می‌کند؛ بُردار مرکزی، بُرداری از دیتاست آموزشی است. بُردار ورودی با بُردار مرکزی مقایسه می‌شود و تفاوت آن‌ها در تابع RBF به کار می‌رود. برای مثال، اگر میان بُردار مرکزی و بُردار ورودی هیچ تفاوتی وجود نداشته باشد، میزان تفاوت برابر با صفر خواهد بود. توزیع نرمال در  x = 0 برابر با 1 است، لذا خروجی نورون نیز 1 خواهد بود.

بُردار «مرکزی» در مرکز تابع RBF قرار دارد، زیر این بردار همان ورودی‌ای‌ است که رأس توزیع را خروجی می‌دهد.

علاوه بر این، در صورت متفاوت بودن بُردارهای ورودی و مرکزی  ، خروجی نورون به صورت نمایی در جهت صفر کاهش می‌یابد. نورون RBF را می‌توان نوعی معیار غیرخطی برای اندازه‌گیری میزان شباهت میان بُردارهای ورودی و مرکزی در نظر گرفت. با توجه به اینکه نورون شعاعی مبتنی بر شعاع است میزان تفاوت بُردار و نه جهت آن اهمیت دارد.

نکته آخر اینکه، آنچه گره‌های RBF آموخته‌اند از طریق یک اتصاال ساده به لایه خروجی، وزن‌دهی و متعاقباً جمع‌ بسته می‌شوند. گره‌های خروجی مقادیر وزنی بزرگی را به نورون‌های RBF، که اهمیت ویژه‌ای در یک دسته دارند، نسبت می‌دهند و در مقابل برای نورون‌هایی که خروجی‌شان اهمیت کمتری دارد، وزن کمتری در نظر می‌گیرند.

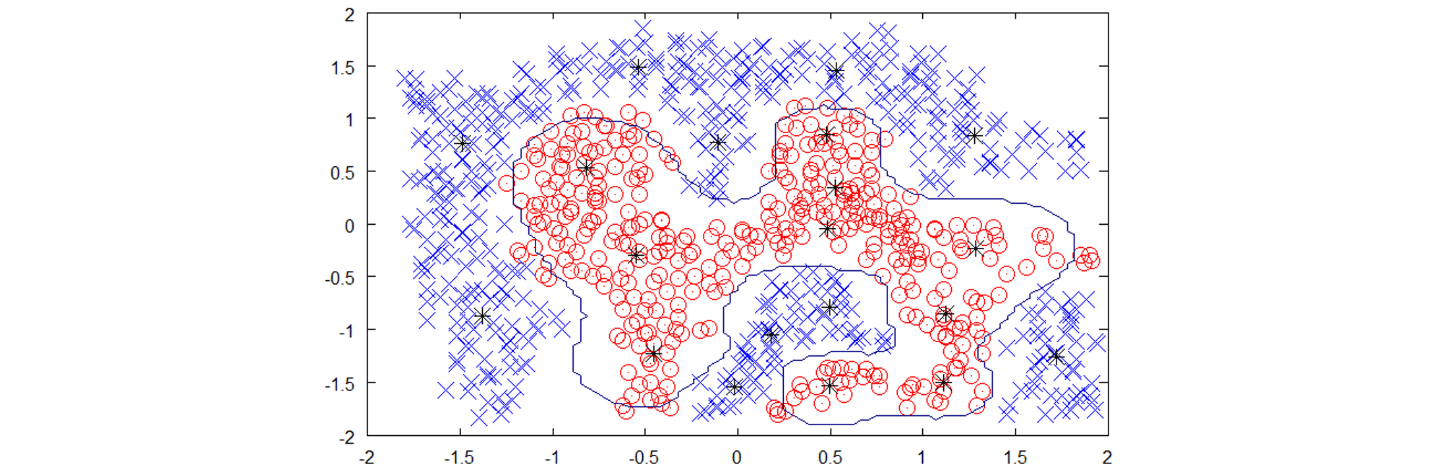
چرا شبکه پایه شعاعی بر پایه «تشابه» مدل‌سازی می‌کند؟ به دیتاست دو بُعدی مقابل توجه کنید؛ در این دیتاست بُردارهای مرکزیِ 20 گره RBF با علامت + نشان داده شده‌اند.

نقشه کانتور  فضای پیش‌بینیِ شبکه آموزش دیده RBF را نشان می‌دهد: تقریباً اطراف تمامی بُردارهای مرکزی ( یا گروهی از بُردارهای مرکزی) یک قله یا دره وجود دارد.  فضای ویژگی این شبکه به وسیله این بُردارها «تعریف می‌شود». تابع جهانی g(x) که پیش از این راجع به آن صحبت کردیم نیز به همین روش و به وسیله توابع RBF که در مرکز هر یک از نقطه‌داده‌ها قرار دارند، تشکیل می‌شود.

ایجاد گره RBF برای تک تک نمونه‌های موجود در دیتاست آموزشی عملاً غیرممکن است (همانند کاری که کرنل انجام می‌دهد)، به همین دلیل شبکه‌های پایه شعاعی با استفاده از بُردارهای مرکزی نمای landscape شبکه را ایجاد می‌کنند. این بُردارهای مرکزی را معمولاً می‌توان با استفاده از الگوریتم‌های خوشه‌بندی (همچون K-Means) و یا نمونه‌برداری تصادفی پیدا کرد.

اگر بخواهیم فضای ویژگی را بر مبنای ارتفاع ترسیم کنیم، نموداری به شکل زیر خواهیم داشت:

شبکه‌های پایه شعاعی به دلیل استفاده از توابع RBF برای حل مسائل طبقه‌بندی رویکرد متفاوتی (در مقایسه با شبکه‌های عصبی استاندارد) اتخاذ می‌کنند؛ توابع RBF را می‌توان معیاری برای اندازه‌گیری میزان چگالی در نظر گرفت. شبکه‌های عصبی استاندارد، داده‌ها را از طریق عملیات‌های خطیِ توابع فعال‌سازی جدا می‌کنند، در مقابل شبکه‌های پایه شعاعی سعی دارند داده‌ها را بر مبنای تبدیلات مبتنی بر «چگالی» گروه‌بندی کنند.

به همین دلیل، شبکه‌های پایه شعاعی معماری ساده و غیرخطی فوق‌‌العاده‌ای دارند و رقیب سرسختی برای شبکه‌های عصبی مصنوعی(Artificial Neural Networks) هستند.

استفاده از توابع RBF به مفهمومی موسم به «درون‌یابی تابع شعاعی» بستگی دارد که یکی از موضوعات پرطرفدارِ نظریه تقریب و یا مطالعه توابع تقریب است.

همان‌گونه که پیش از این نیز گفتیم، توابع RBF این ایده که یک نقطه باید بیشترین تأثیر را در همان نقطه داشته باشد و هر چه بیشتر از آن نقطه فاصله بگیرد، تأثیراتش نیز کاهش پیدا می‌کنند را در قالب معادلات و مباحث ریاضی نشان می‌دهند. از این روی، برای ایجاد غیرخطی‌های پیچیده می‌توان آن‌ها را به روش‌های گوناگونی تغییر داد.

نکات کلیدی

• تابع پایه شعاعی (RBF) تابعی است که بر مبنای فاصله از یک مرکز تعریف می‌شود. در این توابع، موقعیت‌های نسبی (نه موقعیت دقیق) اهمیت دارد.
• این توابع یک ویژگی منحصر به فرد دارند: در مرکز، (تأثیر) خروجی به بالاترین حد ممکن می‌رسد و هر چه از مرکز فاصله بگیریم (در تمامی جهات) تأثیرات کاهش پیدا می‌کنند.
• کرنل‌های RBF یک تابع RBF در مرکز هر یک از نقاط قرار می‌دهند و با انجام عملیات‌های خطی نقاط را به فضاهایی با ابعاد بیشتر نگاشت کنند؛ در این فضاها به سادگی می‌توان نقطه‌ها را جدا کرد.
• شبکه‌های پایه شعاعی معماری‌هایی ساده‌ای با دو لایه هستند؛ یک لایه از نورون‌های RBF و یک لایه از نورون‌های خروجی. به هر یک از نورون‌های RBF یک «بُردار مرکزی» نسبت داده می‌شود که بُردارهای ورودی با آن‌ها مقایسه می‌شوند. این توابع از چگالی استفاده می‌کنند و به همین دلیل می‌توانند غیرخطی‌های پیچیده را با ساختارهای خیلی کوچک، مدل‌سازی کنند.