فراتر از شبکه های عصبی پیچشی در تنسورفلو 2.0

هدفGoal ما از ساخت نخستین مدل شبکه ‌های عصبی پیچشی (ConvNet)، شناسایی سگ‌ها و گربه‌ها بود. ساختار این مدل حاویِ لایه‌های پیچش دوبعدی (Conv2D) و ترکیبی از لایه‌های ادغام و نرمال سازی بسته batch normalization، و dropout می‌باشد. در این راستا از یک لایه مسطح‌ساز flattening layer استفاده می‌شود که نهایتاً لایه تراکم Dense layer را به دنبال دارد. این کار موثر واقع شد و از دقت بسیار خوبی هم برخوردار بود. سپس از همین ساختار جهت طبقه بندی مجموعه‌داده MNIST استفاده کردیم. تنها کاری که باید انجام می‌دادیم این بود که تابع هزینه Loss function را در لایه تراکم از آنتروپی متقابل دوتایی binary cross-entropy به آنتروپی متقابل رسته‌ای categorical cross-entropy تغییر دهیم. به این ترتیب احساس کردیم تسلط بالایی در استفاده از شبکه‌ های عصبی پیچشی داریم. اما راه را اشتباه رفته بودیم، چرا که باید مسائل زیادی را مدنظر قرار دهیم؛ مثل ایجاد ساختارهای متصل پراکنده، انواع مختلفی از لایه‌های Conv2d، به‌کارگیری روش‌های مختلف به منظور جلوگیری از بیش‌برازش overfitting  و….

لایه‌های Conv2D پیشرفته

پیچش‌های تفکیک‌پذیر عمق‌محور (Depthwise Separable Convolutions)

این شبکه‌ها بسیار کارآمد هستند، زیرا به حافظه و محاسبات کمتری احتیاج دارند و در برخی موارد نتایج بهتری به دست می‌آورند. به دلیل داشتن این خصوصیات، معمولا چنین شبکه‌هایی زمانی استفاده می‌شوند که مدل در وسایل Edge/IoT به کار برده می‌شود، چون CPU و RAM محدودی دارند. در این شبکه‌ها، فرایند لایه پیچش عادی به دو فرایند پیچش depth-wise (عمق‌محور) و پیچش point-wise (نقطه‌محور) تقسیم می‌شود.
در پیچش عمق‌محور depthwise convolution، کِرنل kernel یک بار در هر کانال تکرار می‌شود، در حالی که پیچش ‌نقطه‌محور  pointwise convolution از کرنل 1×1 برای افزایش تعداد کانال‌ها استفاده می‌کند. با این کار، تعداد کل ضرب‌های مورد نیاز کاهش می‌یابد و شبکه سریع‌تر می‌شود. در این مقاله اطلاعات ارزشمندی را درباره روش استفاده از چنین شبکه‌هایی ارائه شده است.

(("tensorflow.keras.layers.SeparableConv2D(32, (3, 3), padding="same

پیچش اتساع یافته (Dilated Convolution)

امکان اجرای این نوع پیچش‌ها در لایه‌های پیچشی عادی و همچنین لایه‌های پیچشی تفکیک‌پذیر وجود دارد. پیچش اتساع‌یافته یک نوع عملیات پیچش عادی به حساب می‌آید که شکاف‌هایی دارد. این نوع پیچش علاوه بر ارائۀ میدان پذیرنده بزرگتر، محاسبه کارآمد و مصرف حافظه کمتر، می‌تواند رزولوشن و ترتیب داده‌ها را نیز حفظ کند. بنابراین عملکرد مدل را به طرز چشمگیری بهبود می‌بخشد.

#In Normal Conv2D
tf.keras.layers.Conv2D(32, (3, 3), padding='same', dilation_rate=(2, 2))
#In Seperable Conv2D
tf.keras.layers.SeparableConv2D(no_of_filters, (3, 3), padding='same', dilation_rate=(2, 2))

 

روش Spatial Dropout

در روش dropout عادی، برخی از نرون‌هایی که به طور تصادفی انتخاب شده‌اند، در طول آموزش کنار گذاشته می‌شوند. این نرون‌ها هیچ نقش مثبتی در عملیات «forward pass» ندارند و وزن شان در طول عملیات «backward pass» به‌روزرسانی نمی‌شود. همین موضوع باعث می‌شود شبکه به یادگیری چندین روش درونی مستقل بپردازد و احتمال بیش برازش آن در داده‌های آموزشی کاهش پیدا کند.

اما در روش spatial dropout به جای صرف نظر ار نرون‌ها، کل نگاشت‌های ویژگی کنار گذاشته می‌شوند. در سند Keras راجع به special dropout این چنین بیان شده: اگر پیکسل‌های مجاور درون نگاشت‌های ویژگی همبستگی محکمی با یکدیگر داشته باشند، روش dropout عادی در عملیات فعال‌سازی به نظم‌دهی نمی‌پردازد و از میزان یادگیری موثر کاسته می‌شود. در این مورد، روش spatial dropout به افزایش عدم ‌وابستگی در نگاشت‌های ویژگی کمک می‌کند و استفاده از آن باید در دستور کار قرار گیرد.

tf.keras.layers.SpatialDropout2D(0.5)

 

روش Gaussian Dropout

ترکیب dropout و نویز گاوسی، این روش را می‌سازد. یعنی این لایه علاوه بر حذف برخی نورون‌ها، از نویز گاوسی Gaussian noise ضرب‌پذیر هم استفاده می‌کند. مانند روش dropout عادی، نویز ضرب‌پذیر انحراف معیار sqrt(rate / (1 — rate)) دارد. برای مطالعه بیشتر درباره این روش، می‌توانید مقاله زیر را بخوانید.

tf.keras.layers.GaussianDropout(0.5)

نظم‌دهی فعالیت (Activity Regularization)

عملیات نظم دهی Regularization تغییرات اندکی در شبکه های عصبی پیچشی به وجود می‌آورد تا به شکل بهتری تعمیم یابند. این عملیات، شبکه های عصبی پیچشی را ترغیب می‌کند تا ویژگی‌های پراکنده و نکاتی از دل مشاهدات خام یاد بگیرد. همین موضوع باعث می‌شود مدل به شکل بهتری بر روی داده‌های دیده‌ نشده عمل کند. در بخش زیر، سه روش نظم‌دهی را معرفی می‌کنیم:

• l1: فعالیت به عنوان مجموع مقادیر مطلق محاسبه می‌شود.
• l2: فعالیت به عنوان مجموع مقادیر مجذور محاسبه می‌شود.
• l1_l2: فعالیت به عنوان مجموع مقادیر مطلق و مجموع مقادیر مجذور محاسبه می‌شود.

فرمول‌های نظم‌دهی L1 و L2. لامبدا به عنوان پارامتر نظم‌دهی شناخته می‌شود.
مقدار ماتریس وزن به دلیل افزودنِ عبارتِ نظم‌دهی کاهش می‌یابد و به مدل‌های ساده‌تری می‌رسد که به کاهش بیش‌برازش می‌پردازند. برای دسترسی به اطلاعات بیشتر درباره روش نظم‌دهی، می‌توانید به لینک زیر مراجعه کنید:

#L1 regularization
tf.keras.layers.ActivityRegularization(l1=0.001)
#L2 regularizaton
tf.keras.layers.ActivityRegularization(l2=0.001)
#L1_L2 regularization
tf.keras.layers.ActivityRegularization(l1=0.001, l2=0.001)

معماری‌های پیچیده

معماری های متصل پراکنده(Sparsely Connected Architectures)

دو نوع معماری وجود دارد: متصل متمرکز و متصل پراکنده.

اگر شبکه inception نقش بالایی در محبوبیت این روش داشت، پس چه نیازی به این نوع معماری‌ها بود؟ آیا نمی‌توانستیم به افزودنِ لایه‌ها بسنده کنیم؟ آیا عمیق‌تر شدن شبکه، زمینه را برای حصول نتایج بهتر فراهم نمی‌کند؟ جواب منفی است. هرقدر مدل بزرگتر باشد، بیشتر در معرض بیش‌برازش قرار می‌گیرد؛ به ویژه در مجموعه‌داده‌های کوچکتر. همچنین میزان نیروی محاسباتی لازم برای آموزش چنین شبکه ای افزایش می‌یابد.
گاهی خطای آموزش وضعیت بدتری پیدا می‌کند. در این صورت معماری‌هایی که به شکل پراکنده به هم وصل شده‌اند، می‌توانند در افزایش عمق و عرض مدل‌ها کمک کنند و از شدت نیروی محاسبات بکاهند. این نوع ساختارها می‌توانند اندازه کرنل مختلفی در پیچش داشته باشند که عموماً از tf.keras.layers.add برای ایجاد ساختارهای به‌هم‌پیوسته استفاده می‌شود.

 

from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Conv2D, add, Input
from tensorflow.keras.utils import plot_model
model = Sequential()
model.add(Conv2D(64, (3, 3), activation = 'relu', padding='same', input_shape=(128, 128, 3)))
model.add(Conv2D(64, (3, 3), activation = 'relu', padding='same'))
model.add(Conv2D(128, (3, 3), activation = 'relu', padding='same'))
plot_model(model)

امکان ساخت مدل‌هایی از این دست، با اختصاص متغیر به آن‌ها وجود دارد. شکل ورودی در tf.keras.layers.Input مشخص می‌شود و tf.keras.models.Model برای تعیین ورودی‌ها و خروجی‌ها استفاده می‌شود.

from tensorflow.keras.models import Model
from tensorflow.keras.layers import Conv2D, Input
from tensorflow.keras.utils import plot_model
input_flow = Input(shape=(128, 128, 3))
x = Conv2D(64, (3, 3), activation = 'relu', padding='same')(input_flow)
x = Conv2D(64, (3, 3), activation = 'relu', padding='same')(x)
x = Conv2D(128, (3, 3), activation = 'relu', padding='same')(x)
model = Model(inputs=input_flow, outputs=x)
plot_model(model)

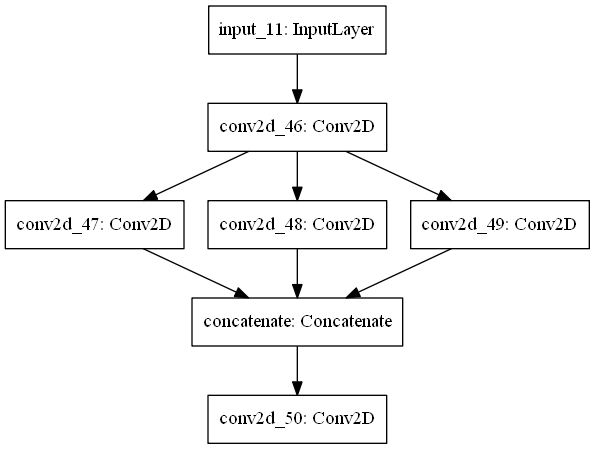
حال برای ایجاد معماری‌های پراکنده، به اختصاص چند لایه به لایه‌های دیگر احتیاج داریم. سپس باید از tf.keras.layers.concatenate برای پیوند دادن آن‌ها استفاده کنیم.

from tensorflow.keras.models import Model
from tensorflow.keras.layers import Conv2D, Input, concatenate
from tensorflow.keras.utils import plot_model
input_flow = Input(shape=(128, 128, 3))
x = Conv2D(64, (3, 3), activation='relu', padding='same', input_shape=(128, 128, 3))(input_flow)
one = Conv2D(64, (3, 3), activation='relu', padding='same')(x)
two = Conv2D(64, (5, 5), activation='relu', padding='same')(x)
three = Conv2D(64, (7, 7), activation='relu', padding='same')(x)
x = concatenate([one, two, three])
x = Conv2D(128, (3, 3), activation = 'relu', padding='same')(x)
model = Model(inputs=input_flow, outputs=x)
plot_model(model)

اتصالات skip

شبکه «ResNet50» بود که باعث محبوبیت این روش شد. هدف اصلی از روش اتصالات skip، حل مسئله ای بود که توسط تیم تحقیقات میکروسافت در مقاله شان با عنوان ” Deep Residual Learning for Image Recognition.” آورده شده بود.
نکته‌ای که باید به آن توجه داشت این است که با افزایش عمق شبکه، دقت اشباع شده و به سرعت کم می‌شود. با کمال تعجب این کاهشِ سرعت ناشی از بیش‌برازش نیست و اضافه کردن لایه‌های بیشتر به مدل عمیق، باعث افزایش خطای آموزش می‌شود.

از مزایای این کار می‌توان به آسان شدن برآورد مقدار وزن‌ها و تعمیمِ بهترِ مدل اشاره کرد.
اگر سازوکار ایجاد ساختارهای پراکنده را به خوبی درک کرده باشید، می‌توانید به راحتی آن را به مرحله اجرا درآورید و از tf.keras.layers.Add استفاده کنید.

from tensorflow.keras.models import Model
from tensorflow.keras.layers import Conv2D, Input, Add
from tensorflow.keras.utils import plot_model
input_flow = Input(shape=(128, 128, 3))
x = Conv2D(64, (3, 3), activation='relu', padding='same', input_shape=(128, 128, 3))(input_flow)
one = Conv2D(64, (3, 3), activation='relu', padding='same')(x)
two = Conv2D(64, (5, 5), activation='relu', padding='same')(one)
three = Conv2D(64, (7, 7), activation='relu', padding='same')(two)
x = Add()([x, three])
x = Conv2D(128, (3, 3), activation = 'relu', padding='same')(x)
model = Model(inputs=input_flow, outputs=x)
plot_model(model)

نتیجه‌‎گیری

استفاده از این مدل‌ها شاید باعث ارتقای مدل‌مان شود، اما همیشه این اتفاق نمی‌افتد. شاید این مدل‌ها حتی در صورت برخورداری از لایه‌های Conv2D عادی هم عملکردی بدتری نسبت به ساختار به‌هم‌پیوسته داشته باشند. باید این مدل‌ها را امتحان کنیم و ببینیم کدام استراتژی بهترین نتایج را به دنبال دارد.