معرفی آلفا، بتا و توان آزمون آماری
یکی از مهارتهای اساسی و ضروری برای هر دانشمند داده، آشنایی با نحوهی اجرای آزمون فرضیه است. در ابتدا شاید درک آلفا alpha، بتا beta، توان آزمون Power (statistical power) و خطاهای نوع اول Type I error و دوم Type II error کار دشواری باشد. در این نوشتار قصد داریم با ارائهی تصاویر مربوطه، اطلاعات بیشتری در این زمینه در اختیار مخاطبان قرار دهیم.
فرض کنید یک طرح آزمایشی داریم که در آن A گروه کنترل و B گروه آزمایش است. فرض اولیه Null hypothesis ما این است که این دو گروه برابر هستند و تغییری که روی گروه B اجرا شده اثر معناداری نداشته است (A=B). فرض مخالف Alternate hypothesis این است که دو گروه مثل هم نیستند و تغییر اعمالشده روی گروه B منجر به تفاوت معناداری شده است (A≠B). توزیعهای حاصل از نمونهگیری را میتوان در چنین شکلی نمایش داد:

سطح اطمینان و آلفا
سطح اطمینان Confidence Level (CL) نشان میدهد برای رد فرض اولیه چقدر باید مطمئن باشیم. به بیان دیگر، میخواهیم چقدر مطمئن باشیم تا بگوییم آزمایش ما (متغیر آزمایشی که روی گروه B اجرا شده) اثر معناداری داشته است؟ سطح اطمینان را باید از قبل مشخص کرد؛ CL به صورت درصد احتمال نشان داده میشود. برای مثال، شاید بخواهید برای رد فرض اولیه، 95% اطمینان داشته باشید. شاید هم بخواهید 99% مطمئن باشید. سطح اطمینان به آزمایش و میزان اهمیت پیامدهای آن بستگی دارد. در کل، مقدار استاندارد سطح اطمینان از 95% شروع میشود.
مقدار آلفا به صورت CL-1 به دست میآید. پس اگر سطح اطمینان 95% باشد، آلفا 0/05 یا 5% خواهد بود. آلفا، احتمال رد فرض اولیه در صورت درست بودن آن را نشان میدهد. به عبارت دیگر، اگر آلفا 5% باشد، یعنی میتوانیم 5% احتمال این که نتیجهگیری ما (مبنی بر وجود تفاوتی که در اصل وجود ندارد) اشتباه باشد را قبول کنیم. این خطا را به نام خطای نوع I (خطای نوع یک) نیز میشناسند. برای درک بهتر به تصویر رجوع میکنیم:

سطح اطمینان/مقدار آلفا یک مرز تصمیمگیری Decision boundary ایجاد میکنند. مقادیری که بالاتر از این محدوده باشند بخشی از توزیع B در نظر گرفته میشوند و از فرض مخالف حمایت میکنند. مقادیری هم که پایینتر از این محدوده باشند، جزء توزیع A به شمار رفته و از فرض اولیه حمایت میکنند. در تصویر بالا، قسمت سایهخورده نشاندهندهی مقدار آلفا است، یعنی مقادیری که در صورت جایگذاری اشتباه در توزیع B، همچنان قابل قبول خواهند بود. تعیین این مرز تصمیمگیری و آمادگی برای پاسخهای اشتباه، الزامی است؛ زیرا بین این دو توزیع مقداری همپوشانی وجود دارد که میتواند ابهامآور باشد. قسمت سایهخورده مقادیری از برچسب حقیقی داده ها هستند که از فرض اولیه پشتیبانی میکنند (توزیع A)، اما ما آنها را به اشتباه در حمایت از فرض مخالف (توزیع B) در نظر میگیریم. به همین دلیل آنها را مثبت کاذب False positive مینامیم؛ چون به اشتباه از پاسخ مثبت پشتیبانی میکنند. برای واضحتر کردن مبحث یک مثال میزنیم. فرض کنید سطح اطمینان 95% و آلفا 5% است؛ این بدین معنی است که ناحیهی سایهخوردهای که در تصویر بالا مشخص شده 5% از ناحیهی زیر منحنی A را به خود اختصاص میدهد.
توان آزمون آماری و بتا
توان یک فرض آزمایشی برابر است با احتمال این که به درستی از فرض مخالف حمایت کند. به بیان دیگر، توان آزمون نشان میدهد چقدر احتمال دارد که ورودیها (دادههای آزمایشی) که در توزیع B قرار میگیرند، به درستی تشخیص داده شده باشند؟ توان آزمون به صورت beta-1 محاسبه میشود. بتا احتمال پذیرش فرض اولیه است حتی اگر فرض مخالف درست باشد. یعنی احتمال اینکه یک مقدار را به اشتباه جزئی از توزیع A در نظر بگیریم، در حالیکه واقعاً متعلق به توزیع B است. معیار استاندارد توان آزمون اغلب 0/8 یا 80% است، در نتیجه بتا هم معمولاً 0/2 یا 20% در نظر گرفته میشود. علاوه بر موارد قبلی، سطح بتا را نیز باید متناسب با آزمایش خود تعیین کنید. تصویر زیر در تشخیص بتا به شما کمک میکند:
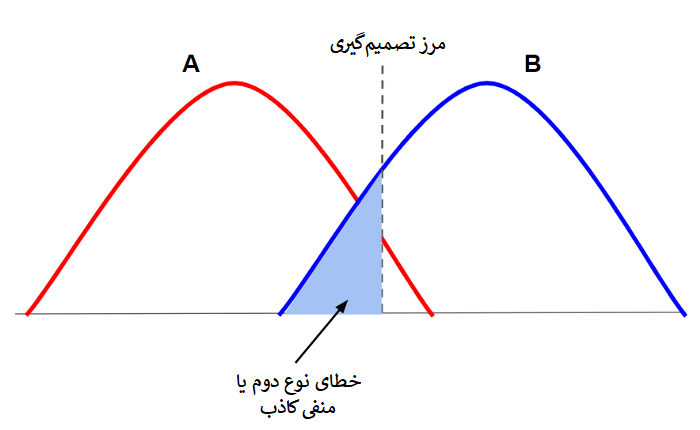
ناحیهی سایهخورده نشاندهندهی بتا است. همانطور که در تصویر میبینید، این مقادیر در توزیع A قرار گرفتهاند (در پشتیبانی از فرض اولیه) در حالیکه باید بخشی از توزیع B باشند و بدین ترتیب اثری منفی روی نتیجهی آزمایش میگذارند. به همین دلیل، دادههای این ناحیه را منفی کاذب False negative میخوانیم. این خطای آزمایشی را به نام خطای نوع II (خطای نوع دو) نیز میشناسند.
جمعبندی

بعد از آشنایی با آلفا و بتا، احتمالاً متوجه توازنی که بین آنها وجود دارد شدهاید. اگر بخواهیم از مثبتهای کاذب یا خطای نوع I اجتناب کنیم، باید سطح اطمینان را بالا ببریم. اما هرچه در پرهیز از مثبتهای کاذب مصرتر باشیم، احتمال ایجاد منفیهای کاذب یا خطای نوع دوم را افزایش میدهیم. چند نکته هستند که برای حل این مشکل باید مدنظر داشته باشید:
- با توجه به طرح آزمایشی خود، تصمیم بگیرید کدام نوع خطا برایتان بدتر است. برای مثال، فرض کنید میخواهید آزمایش کووید-19 را اجرا کنید. اگر قرار باشد فردی را از نظر ابتلا به کووید-19 آزمایش کنید، منفی کاذب بدتر از مثبت کاذب است، چون به فردی که این ویروس را دارد گفته میشود سالم است (منفی کاذب) و این فرد میتواند بقیه را هم مبتلا کند، چون فکر میکند بیمار نیست. پس در چنین مسئلهای بهتر است به اشتباه پیشبینی کنیم افراد مبتلا به این بیماری هستند (مثبت کاذب)، چون بدترین چیزی که میتواند رخ دهد این است که در خانه میمانند و خود را قرنطینه میکنند. پس در آزمایش کووید-19، اولویت باید پایین بودن مقدار بتا باشد. اما از طرف دیگر، شاید یک شرکت بخواهد آزمایشی انجام دهد که در آن آلفا یا خطای نوع اول باید کمتر باشد، چون اعمال متغیر آزمایشی پرهزینه بوده و خطرات زیادی دارد که باعث میشود اجرای آن به صرفه نباشد، مگر اینکه تقریباً کاملاً مطمئن باشند اثر مثبتی خواهد داشت. با بررسی مسئلهی خاصی که در دست دارید میتوانید خطایی که بیشترین اهمیت را برای شما دارد به حداقل یا حداکثر برسانید.
- حداقل تفاوت معنادار را برای مسئلهی خود مشخص کنید. فرض کنید میخواهید ببینید تغییری که در یک وبسایت اعمال شده، نرخ بازدید را افزایش داده است یا خیر. اگر تغییری که در نرخ بازدید رخ داده کوچک باشد، تشخیص تفاوت در آزمون فرضیه سختتر و احتمال اینکه مرتکب خطا شوید بیشتر خواهد بود. اگر آستانهای تنظیم کنید که نشان دهد مقدار تفاوت باید چقدر باشد تا ارزش اعمال تغییر را داشته باشد، همپوشانی کمتری بین دو توزیع وجود خواهد داشت، بدین ترتیب ناحیهی ابهام و خطا کوچکتر میشود. پس، اگر تغییر مشاهدهشده در آزمایشات خیلی کوچک باشد، احتمال ارتکاب اشتباه افزایش مییابد، چون همپوشانی بین دو توزیع بیشتر خواهد بود.
- اندازهی نمونهها را افزایش دهید. افزایش نمونهها تشخیص تفاوت بین دو توزیع را آسانتر میکند. علاوه بر این، اگر تفاوتهای کوچک در آزمایش شما اهمیت دارند، افزایش اندازهی نمونهها راهکار مناسبی است چون به تشخیص این تفاوتهای کوچک کمک میکند. با استفاده از ماشینحسابهای خاصی که روی اینترنت هم در دسترس هستند، میتوانید بر اساس آلفا، توان آزمون و حداقل اندازه اثر Effect size، اندازهی بهینه برای نمونهی آزمایشی خود را پیدا کنید.