همبستگی و معرفی معیار بهتری برای آن: همبستگی فاصله‌ای

احتمالاً همه بر سر این موضوع توافق نظر دارند که یکی از پرکاربردترین معیارها در مشاغل، همبستگی، یا به بیان دقیق‌تر، همبستگی‌‌‍‌‌‌‌‌‌ پیرسون (Pearson Correlation) است.

یادآوری: همبستگی‌‌‌‌‌ رابطۀ خطی بین دو متغیر را اندازه می‌گیرد. مسئله این است که بسیاری از روابط خطی نیستند.

مثلاً، شاید در نتیجۀ محاسبات به این نتیجه برسید که بین متغیر X و درآمد همبستگی وجود ندارد، درحالی‌که واقعاً اینطور نیست. شاید این دو متغیر همبستگی داشته باشند، فقط این همبستگی‌‌‌‌‌ غیرخطی باشد. اینجاست که همبستگی فاصله‌ای به کمکمان می‌آید.

همبستگی فاصله‌ای چیست؟

همبستگی فاصله‌ای معیار قوت وابستگی بین دو متغیر تصادفی غیرخطی است. این معیار از همبستگی پیرسون فراتر می‌رود، زیرا تنها به اندازه‌گیری وابستگی‌های خطی محدود نمی‌شود و می‌تواند به صورت چندبُعدی کار کند. مقدار همبستگی فاصله‌ای عددی بین 0 تا 1 است، 0 حاکی از استقلال دو متغیر X و Y است و 1 نشان می‌دهد زیرفضاهای خطی (Linear Subspace) X و Y برابر هستند.

تصویر پایین همبستگی‌‌‌‌‌ فاصله‌ای را در مقایسه با همبستگی پیرسون نشان می‌دهد.

فرمول محاسبۀ همبستگی‌‌‌‌‌ فاصله‌ای از قرار ادامه است:

همبستگی‌‌‌‌‌ فاصله‌ای همبستگی بین خود فواصل را نشان نمی‌دهد، بلکه همبستگی‌‌‌‌‌ بین ضرب‌های داخلی (Scalar Product) است که مولد ماتریس‌هایی هستند که جمع درایه‌های هر سطر و ستونشان صفر است، به این ماتریس‌ها double-centered می‌گویند.

مبنای ریاضی

فرض کنید (Xk, Yk), k= 1, 2, …, n یک نمونۀ آماری از دو متغیر تصادفی X و Y باشد.

ابتدا، ماتریس‌های فاصله‌ای (aj, k) و (bj, k) با ابعاد n در n محاسبه می‌شوند، این ماتریس‌ها شامل فاصلۀ بین همۀ جفت درایه‌‌ها هستند.

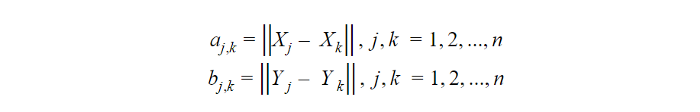
سپس فواصل double-centered محاسبه می‌شوند:

از چشم‌انداز بصری، با محاسبۀ فواصل double-centered، نمایش ماتریسی (در سمت چپ) به طرح سمت راست (ماتریس double-centered) تبدیل می‌شود.

چرا این عملیات انجام می‌شود؟

کوواریانس‌ ضرب خارجی (Cross-product) گشتاورها (Moment) است. از آنجایی که فواصل گشتاور نیستند، باید آنها را برحسب گشتاور محاسبه کرد. برای محاسبۀ این گشتاورها، ابتدا باید انحراف از میانگین (Deviation from the Mean) را محاسبه کرد، یعنی همان کاری که double-centering انجام می‌دهد.

در نهایت، میانگین حسابی (Arithmetic Average) حاصلضرب A و B محاسبه می‌شود تا مربع کوواریانس فاصله‌ای نمونه (Squared Sample Distance Covariance) به دست آید:

واریانس فاصله‌ای در واقع کواریانس فاصله‌ایِ دو متغیر یکسان است. پس از جذر این معادله به دست می‌آید:

پیاده‌سازی در پایتون

در صورتی که قصد دارید از معیار همبستگی فاصله‌ای استفاده کنید، خوشبختانه، کتابخانه‌ای در پایتون وجود دارد که امکان پیاده‌سازی آن را بسیار ساده می‌کند.

یک نمونه از کد اسنیپت (Snippet) در پایتون را در این قسمت مشاهده می‌کنید:

import dcordef distance_correlation(a,b):
    return dcor.distance_correlation(a,b)

با این تابع به‌راحتی می‌توانید همبستگی‌‌‌‌‌ فاصله‌ای بین دو نمونۀ a و b را محاسبه کنید.