
مقایسه مقیاسبندی و نرمالسازی داده
در فرایند اکتشاف دادهها و ساخت مدل، روشهای گوناگونی برای انجام مسائل وجود دارند که انتخاب و کاربردشان به هدف و تجربه متخصص بر میگردد.
برای نمونه، نرمالسازی داده را میتوان با روش L1 (معیار فاصله منهتن Manhattan distance )، L2 (معیار فاصله اقلیدسی Euclidean distance ) یا ترکیبی از این دو روش انجام داد.
در حوزه علوم داده، جایجایی اصطلاحات با یکدیگر امری متداول است. روش (method) و تابع (function) دو عبارتی هستند که اغلب به جای یکدیگر استفاده میشوند. معنای این دو کلمه به هم شباهت دارد؛ اما رفتار آنها متفاوت است؛ توابع شامل یک یا چند پارامتر میشوند، اما روشها معمولاً اشیائی را فراخوانی میکنند:
print(‘hello’) # function
df.head() # method
در خصوص کلمات میانگین (mean) و حد وسط (average) نیز همین موضوع دیده میشود. این دو کلمه را بسیاری اوقات به جای هم به کار میبرند. بااینحال، اصطلاح تخصصی میانگین، میانگین حسابی Arithmetic mean است و حد وسط عملاً یک موقعیت مرکزی است؛ اما در کل، افرادی که تخصصی در آمار ندارند، از کلمه حد وسط بهعنوان میانگین حسابی نیز استفاده میکنند. (openstax.org)
مورد دیگر از این عبارات مشابه، مقیاسبندی scaling و نرمالسازی Normalizing هستند که اغلب به جای یکدیگر به کار برده میشوند. این دو مفهوم شباهت زیادی به هم دارند.
شباهتها

در هر دوی این عملیاتها، مقادیر متغیرهای عددی بهنحوی تغییر مییابند که نقاط تغییریافته ویژگیهای خاص مفیدی داشته باشند. این ویژگیهای خاص سپس برای ایجاد ویژگیها(features) و مدلهای بهتر به کار میروند.
تفاوتها

در مقیاسبندی، دامنه توزیع دادهها را تغییر میدهیم؛ اما در نرمالسازی، شکل توزیع دادهها را تغییر میدهیم.
دامنه range به تفاوت بین کوچکترین و بزرگترین مؤلفه موجود در توزیع گفته میشود.
مقیاسبندی و نرمالسازی آنقدر به هم شباهت دارند که گاهی آنها را به جای یکدیگر اجرا میکنند؛ اما همانطور که از تعریف آنها متوجه شدیم، تأثیری که روی دادهها اعمال میکنند، متفاوت است. ما بهعنوان متخصصان علوم داده، باید این تفاوتها را درک کنیم و از آن مهمتر، بدانیم چه زمانی از کدام روش استفاده کنیم.
چرا دادهها را مقیاسبندی میکنیم؟
همانطور که گفته شد، در مقیاسبندی، دادهها را طوری تغییر میدهیم که در یک مقیاس مشخص (مثلاً 100-0 یا عمدتاً 1-0) جای بگیرند؛ بهخصوص در مواقعی که از روشهای مبتنی بر فاصله نقاط از هم استفاده میکنید، باید عملیات مقیاسبندی را انجام دهید.
برای مثال، وقتی میخواهید از روش SVM (ماشین بردار پشتیبانی Support vector machines ) یا الگوریتمهای خوشهبندی (مثل KNN یا K همسایه نزدیک K-nearest neighbours ) استفاده کنید، مقیاسبندی دادهها لازم خواهد بود.
در این الگوریتمها، به «یک واحد» تغییر در همه ویژگیهای عددی، به یک اندازه اهمیت داده میشود. برای درک بهتر این موضوع، مثالی از Kaggle را به کار میبریم.
فرض کنید در حال بررسی قیمت یک سری محصولات به ین ژاپن و دلار آمریکا هستید. یک دلار آمریکا تقریباً برابر با 100 ین است. اگر قیمتها را مقیاسبندی نکنید، الگوریتمهایی همچون KNN یا SVM تفاوت یک ینی را برابر با تفاوت یک دلاری در نظر میگیرند.
این موضوع با دانش ما از دنیای واقعی همخوانی ندارد. پس باید دادهها را برای مسائل یادگیری ماشینی مقیاسبندی کنیم، تا دامنه توزیع برای همه متغیرها برابر باشد و بدین ترتیب از چنین مسائلی جلوگیری شود.
با مقیاسبندی متغیرها، امکان مقایسه متغیرهای متفاوت بر مبنای یکسان میسر میشود. (Kaggle)
روشهای مقیاسبندی متداول
مقیاسبندی ویژگی ساده
def simple_feature_scaling(arr):
"""This method applies simple-feature-scaling
to a distribution (arr).
@param arr: An array or list or series object
@return: The arr with all features simply scaled
"""
arr_max = max(arr)
new_arr = [i/arr_max for i in arr]
return new_arr
# Let's define an array arr
arr = list(range(1,11))
arr_scaled = simple_feature_scaling(arr)
print(f'Before Scaling...\n min arr is {min(arr)}\n max arr is {max(arr)}\n')
print(f'After Scaling...\n min arr_scaled is {min(arr_scaled)}\n max arr_scaled is {max(arr_scaled)}')
>>
```
Before Scaling...
min arr is 1
max arr is 10
After Scaling...
min arr_scaled is 0.1
max arr_scaled is 1.0
```

این روش هر مقداری را بر مقدار بیشینه همان ویژگی تقسیم میکند. حاصل این معادله، مقداری بین صفر و یک خواهد بود.
مقیاسبندی ساده ویژگی را میتوان روی دادههای تصویری به کار برد. برای مقیاسبندی تصاویر، آنها را بر 255 (حداکثر تراکم پیکسلی تصویر Maximum image pixel intensity ) تقسیم میکنیم.
در این قسمت، نحوه تعریف یک تابع مقیاسبندی ساده ویژگی را مشاهده میکنید:
همانطور که میبینید، دامنه توزیع به سادگی مقیاسبندی شد و از [1,10] به [0.1, 1] تغییر یافت.
مقیاسبندی کمینه–بیشینه

این روش از مقیاسبندی ویژگی ساده، محبوبتر است. این مقیاسبند (Scaler) مقدار کمینه را از هر کدام از مقادیر کم میکند و بر تفاضل بین بیشینه و کمینه تقسیم میکند.
اینجا یک تابع کمینه-بیشینه تعریف میکنیم:
def min_max_scaling(arr):
"""This method applies min-max-scaling
to a distribution (arr).
@param arr: An array or list or series object
@return: The arr with all features min-max scaled
"""
arr_max = max(arr)
arr_min = min(arr)
range_ = arr_max - arr_min
new_arr = [(i-arr_min)/range_ for i in arr]
return new_arr
# Let's define an arr and call the min-max scaler
arr = list(range(1,11))
arr_scaled = min_max_scaling(arr)
print(f'Before Scaling...\n min arr is {min(arr)}\n max arr is {max(arr)}\n')
print(f'After Scaling...\n min arr_scaled is {min(arr_scaled)}\n max arr_scaled is {max(arr_scaled)}')
>>
```
Before Scaling...
min arr is 1
max arr is 10
After Scaling...
min arr_scaled is 0.0
max arr_scaled is 1.0
```
دقیقاً همچون مثال قبلی، در نتیجه مقیاسبندی کمینه-بیشینه نیز توزیعی با دامنه [1,10] به توزیعی با دامنه [0.0, 1] تبدیل میشود.
اجرای مقیاسبندی روی یک توزیع
در این قسمت، میخواهیم از یک دیتاست استفاده کنیم و عملیات مقیاسبندی را روی یک ویژگی عددی از این دیتاست اجرا کنیم. بدینمنظور، دیتاست مشریان وام اعتباری بانک Credit-One را به کار میبریم.
import pandas as pd import numpy as np from mlxtend.preprocessing import minmax_scaling import seaborn as sns import matplotlib.pyplot as plt from scipy import stats # I define additional NAN values for pandas to check for additional_nan_values = ['n/a', '--','?','None','Non','non','none'] # Save the data link data = 'https://github.com/Lawrence-Krukrubo/Machine_Learning/blob/master/Loan_Data%20for%20Classification.xlsx?raw=true' # Read in the data loan_df = pd.read_excel(data, header=2, na_values=additional_nan_values) loan_df.head()
این بار از تابع minmax_scaling از mlxtend.preprocessing استفاده میکنیم. چند ردیف اول دیتاست را در این تصویر مشاهده میکنید:

در این مثال، میخواهیم دادههای ستون سن را مقیاسبندی کنیم.
همانطور که در تصویر پایین مشاهده میکنید، پایینترین سن موجود در دیتاست اصلی 19 و حداکثر سن 75 بوده است. اما بعد از مقیاسبندی این مقادیر به ترتیب برابر با 0 و 1 شدهاند.

تنها چیزی که با مقیاسبندی تغییر میکند، دامنه توزیع است؛ شکل و سایر خواص توزیع ثابت باقی میمانند.
چرا دادهها را نرمالسازی میکنیم؟
نرمالسازی، نوعی تبدیل ریشهای است. هدف از نرمالسازی تغییر مشاهدات بهنحوی است که قابلتوصیف از طریق یک توزیع نرمال Normal distribution باشند. (Kaggle)
توزیع نرمال یا منحنی زنگولهای Bell curve یک توزیع آماری خاص است که در آن مشاهدات به میزان تقریباً برابر در دو طرف (بالا و پایین) میانگین قرار میگیرند؛ در این توزیع، نما، میانه و میانگین بر هم منطبقاند و بیشتر مشاهدات در نزدیکی این نقطه قرار دارند. توزیع نرمال را با نام توزیع گاوسی نیز میشناسند.

اگر میخواهید از تکنیکهای آماری یا یادگیری ماشینی استفاده کنید که مفروضه اساسی آنها توزیع نرمال دادههاست، باید دادهها را نرمالسازی کنید. برای نمونه، تحلیل خطی افتراقی Linear Discriminant Analysis (LDA) و بیز ساده گاوسی Gaussian naïve bayes چنین مفروضهای دارند.
نکته کمکی: هر روشی که در اسم آن «گاوسی» وجود دارد، به احتمال زیاد مفروضه نرمال بودن توزیع دادهها را دارد.
باید به این نکته توجه داشته باشید که در برخی از ژورنالهای آماری، به نرمالسازی، استانداردسازی نیز گفته میشود. هدف از استانداردسازی، نرمالسازی توزیع بر اساس فاصله هر مشاهده از میانگین بر حسب انحراف معیار است. یک نمونه از روشهای استانداردسازی، نمرات Z هستند.
روشهای نرمالسازی متداول
نمره Z یا نمره استاندارد
از هر کدام از مقادیر موجود در توزیع، میانگین را کم میکنیم؛ سپس حاصل را بر انحراف معیار تقسیم میکنیم. در نتیجه، مقادیری بین 3- تا 3 (شاید کمتر یا بیشتر) به دست میآیند.

این عملیات را بهراحتی میتوان به شکل کد درآورد. ابتدا روش نمره Z را تعریف میکنیم:
def z_score_norm(arr):
"""Apply z-score normalization
to an array or series
"""
mean_ = np.mean(arr)
std_ = np.std(arr)
new_arr = [(i-mean_)/std_ for i in arr]
return new_arr
نرمالسازی باکس–کاکس

روش باکس-کاکس، تبدیلاتی است که روی یک متغیر وابسته با توزیع غیرنرمال انجام میشود، تا آن را به شکل نرمال درآورد. نام تبدیل باکس-کاکس از جورج باکس و سردیوید راکسبی کاکس، دو آماردانی که در سال 1964 با همکاری یکدیگر این تکنیک را خلق کردند، گرفته شده است.
کارکرد
محور روش نرمالسازی باکس-کاکس مؤلفهای به نام لامبدا (λ) است که میتواند مقداری بین 5- تا 5 داشته باشد. از بین همه مقادیر λ، مقدار بهینه برای دادههای موجود انتخاب میشود؛ مقدار بهینه مقداری است که منجر به بهترین برآورد از یک منحنی توزیع نرمال شود.
افرادی که پیشزمینهای در یادگیری ماشینی دارند، احتمالاً متوجه شباهت این فرایند با تنظیم آلفا یا α (نرخ یادگیری) میشوند که به منظور برازش بهتر مدل بر روی دادهها انجام میگردد.
روش باکس-کاکس به صورت پیشفرض تنها برای مقادیر مثبت به کار میرود؛ اما نسخهای از آن وجود دارد که میتواند مقادیر منفی را نیز برآورد کند.
اجرای نرمالسازی روی یک توزیع
در این مثال نیز از دیتاست متقاضیان وام اعتباری بانک Credit-One استفاده میکنیم. این بار تبدیل باکس-کاکس را روی ستون سن اجرا میکنیم. بدین منظور از تابع boxcox() کتابخانه scipy.stats استفاده میکنیم.
from scipy import stats
# let's normalize the data
original_data = loan_df.Age
normalized_data = stats.boxcox(original_data)
# plot both together to compare
fig, ax = plt.subplots(1,2, figsize=(10,5))
sns.set_style('ticks')
sns.distplot(original_data, ax=ax[0])
ax[0].set_title("Original Data")
sns.distplot(normalized_data[0], ax=ax[1])
ax[1].set_title("normalized data")
ax[1].set_xlabel('Age')
plt.show()
خروجی تابع boxcox()، یک مجموعه است که جزء اول آن، سریهای نرمالسازی شده است. حداقل سن در دیتاست اصلی 19 و حداکثر سن آن 75 بود؛ اما در دیتاست نرمالسازیشده، حداقل سن 300/1 و حداکثر آن 4301/1 است.

توجه داشته باشید که اینجا، علاوه بر تغییر دامنه توزیع متغیر سن، شکل توزیع نیز به صورت ریشهای و اساسی تغییر کرده و تقریباً شبیه یک منحنی زنگولهای شده است.
نکات کلیدی
- همواره به دادهها، توزیع و شکل آنها توجه داشته باشید. بدین منظور از نمودار هیستوگرام، Displot یا حتی یک نمودار خطی استفاده کنید.
- به صورت کلی، میتوان گفت اگر میخواهید از یک تکنیک آماری یا یادگیری ماشینی استفاده کنید که مفروضه آن نرمال بودن توزیع دادهها است (برای مثال، تحلیل خطی افتراقی یا LDA یا بیز ساده گاوسی)، باید دادهها را نرمالسازی کنید. روشهایی که در نامشان «گاوسی» یا «نرمال» وجود دارد، اغلب مفروضه نرمال بودن دادهها را دارند. این گروه شامل تکنیکهای کاهش بعد Dimensionality reduction همچون PCA نیز میشود.
- زمانی که از روشهای مبتنی بر فاصله نقاط استفاده میکنید (همچون SVM یا ماشین بردار پشتیبانی و KNN یا K همسایه نزدیک)، باید دادههای خود را مقیاسبندی کنید. حتی اگر تنها میخواهید متغیرها را در یک بازه یکسان قرار دهید، تا هیچ کدام نسبت به دیگری برتری نداشته باشد نیز میتوانید از این عملیات استفاده کنید.
- با مقیاسبندی متغیرها، میتوان به مقایسه آنها بر یک مبنای مشترک کمک کرد.
- اگر مطمئن نیستید باید نرمالسازی انجام دهید یا مقیاسبندی، میتوانید از شکل توزیع دادهها کمک بگیرید.
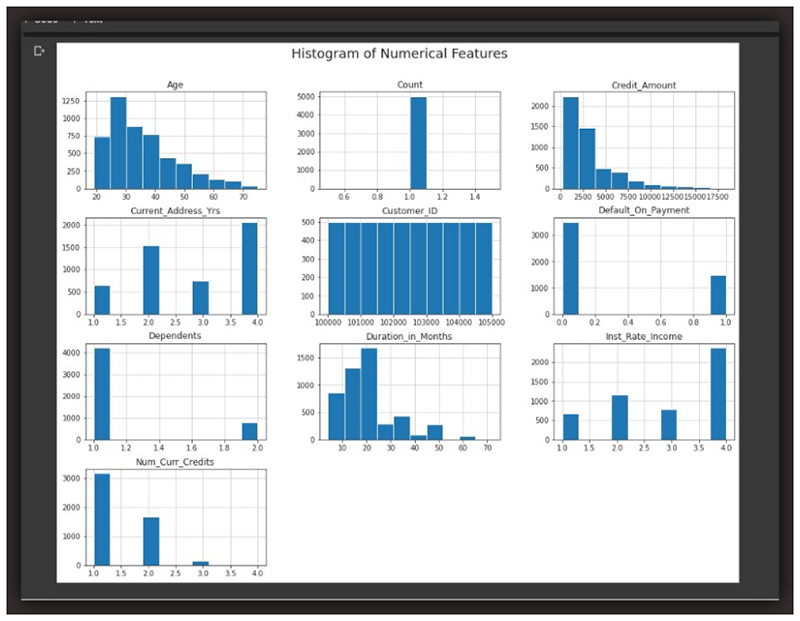
برای مثال، با نگاه به نمودارهای هیستوگرام شبیه به نمودارهای شکل بالا، بهراحتی میتوان فهمید متغیرهایی که تقریباً متقارن هستند یا شکلی شبیه به منحنی زنگولهای دارند (حتی اگر کاملاً متقارن نباشند و مقداری کجی skewness نیز داشته باشند) باید نرمالسازی شوند. از جمله این متغیرها میتوان به سن، مقدار اعتبار، و مدت زمان بر حسب ماه، اشاره کرد.
در سوی دیگر، متغیرهایی که تفاوت زیادی دارند، متمایز از هم هستند، تکمُدی unimodal و غیرمتقارن هستند (برای مثال، تعداد یک متغیر، میزان پرداخت پیشفرض یا نرخ سود) باید مقیاسبندی شوند.
مصورسازی در EDA (تحلیل اکتشافی داده Explorative data analysis ) گامی ضروری است. اگر displot یا نمودار هیستوگرام را داشته باشید، بهراحتی میتوانید ببینید برخی توزیعها متقارن و تقریباً نرمال هستند و بنابراین باید نرمالسازی شوند (مگر اینکه دلیلی مبنی بر عدمانجام این عملیات داشته باشید). در خصوص شکلهای نامتقارن و تکمدی نیز میدانید که باید از طریق روشهای کمینه-بیشینه یا ویژگی ساده، مقیاسبندی انجام دهید.





