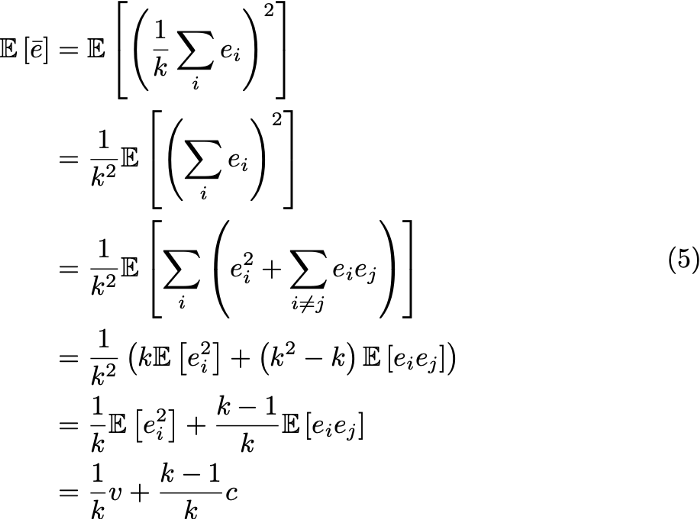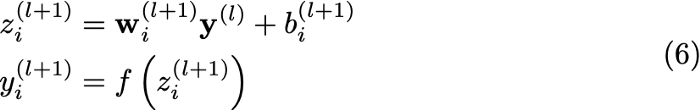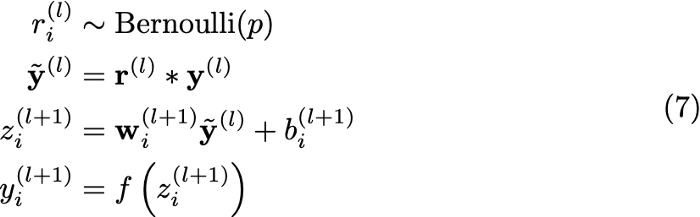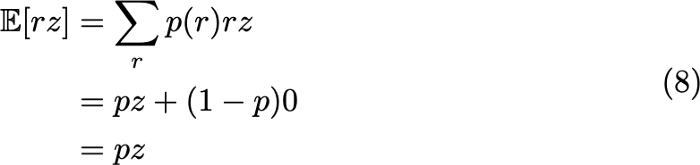آشنایی با مفهوم Dropout ؛ لایه‌ای مفید و رمزآلود در آموزش شبکه‌های عصبی

Dropout لایه مفید و رمزآلودی در آموزش شبکه های عصبی است. Dropout روشی برای منظم‌سازیRegularization  است و خطای تعمیم‌پذیریGeneralization error  را  با کاهش گنجایش مدلModel capacity  کمتر می‌کند؛ بدین ترتیب که در هر دور آموزشی، به جای استفاده از همه‌ نورون‌ها، تنها برخی از نورون‌ها (با احتمال p) فعال می‌شوند. در این نوشتار نحوه‌ کارکرد و پیاده‌سازی Dropout را توضیح می‌دهیم.

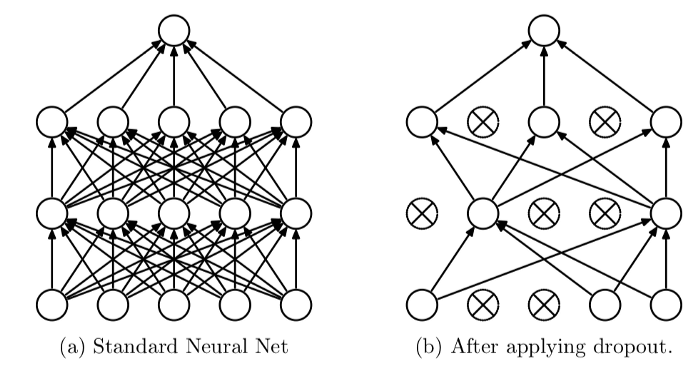
منظم‌سازی(regularization)

مقدار خطایی که شبکه‌های عصبی روی داده‌های آموزشی به دست می‌آورند بسیار کمتر از خطای آن‌ها روی داده‌های آزمایشی است؛ به همین دلیل در معرض بیش‌برازشoverfitting  قرار می‌گیرند. برای مقابله با این مسئله، از تکنیک منظم‌سازی استفاده می‌کنیم تا گنجایش مدل را کاهش دهیم. بدین ترتیب تفاوت بین خطای آموزش و آزمایش کاهش یافته و مدل در مراحل آموزش و آزمایش، عملکرد مشابهی از خود نشان خواهد داد.

هنگام یادگیری شبکه‌های آموزشی باید با تغییر پارامترهای وزن، تابع زیان L را به حداقل رساند. به عبارت دیگر، مسئله‌ بهینه‌سازی، به حداقل رساندن L است.

در منظم‌سازی، تابع منظم‌سازی وزن‌دهی شده را به تابع زیان اضافه می‌کنیم تا مدل بهتر شرطی شده و ثبات بیشتری به دست آورد.

در این معادله، ? پارامترهای منظم‌سازی و R(?) تابع منظم‌سازی است. یکی از پرکاربردترین تکنیک‌های منظم‌سازی، منظم‌سازی L2 یا تجزیه‌ وزنWeight decay  است که از نُرم l2 وزن‌ها به عنوان تابع نرمال‌سازی استفاده می‌کند؛ این منظم‌سازی را بدین صورت می‌توان نشان داد:

در این فرمول، w وزن است. معمولاً سوگیری را وارد معادله نمی‌کنیم چون می‌تواند به عملکرد مدل آسیب زده و منجر به کم‌برازش شود.

مدل‌های گروهی

یک روش برای کاهش خطای تعمیم پذیری، ترکیب چندین مدل مختلف است که اغلب به عنوان «مدل‌های ترکیبیModel ensemble » یا «میانگین‌گیری مدلModel averaging » می‌خوانیم. هر مدلی ممکن است در یک قسمت از داده‌های آموزشی خود مشکل یا خطایی داشته باشد که با خطای مدل‌های دیگر متفاوت است. منطق تکنیک مدل‌های گروهی این است که با ترکیب چند مدل می‌توان مدلی مقاوم‌تر به دست آورد؛ چون قسمت‌هایی که در بیشتر مدل‌ها درست بوده‌اند تغییر نخواهند کرد و خطا کاهش خواهد یافت. بدین ترتیب، مدل‌ میانگین عملکردی حداقل برابر با مدل‌های تشکیل‌دهنده خواهد داشت.

برای مثال، فرض کنید k مدل را که هریک خطای  دارند آموزش می‌دهیم. اگر واریانس خطاها را با v و کوواریانس آن‌ها را با X نشان دهیم، خطای میانگین‌گیری از k مدل بدین طریق به دست می‌آید:

خطای مجذورات موردانتظار برای خطای مدل میانگین نیز برابر خواهد بود با:

همانطور که مشاهده می‌کنید، اگر خطاها کاملاً همبستگی داشته باشند، v با c برابر بوده و خطای میانگین مجذوراتMean squared error  مدل‌ها به v کاهش خواهد یافت. از سوی دیگر، اگر بین خطاها هیچ همبستگی وجود نداشته باشد، c=0 و خطای میانگین مجذورات برابر با (1/k)v خواهد بود. پس می‌توان نتیجه گرفت خطای مجذورات موردانتظار با اندازه‌ گروه (مدل‌های حاضر در گروه) رابطه‌ عکس دارد.

با این حال، آموزش تعداد زیادی مدل، به خصوص شبکه های عصبی عمیق، از نظر محاسباتی هزینه‌بر است. این مشکل فقط مختص مرحله‌ آموزش نیست، بلکه افزایش تعداد مدل‌ها در مرحله‌ استنتاج نیز منجر به افزایش هزینه‌ محاسبات می‌شود. بنابراین، میانگین‌گیری از تعداد زیادی شبکه‌ عصبی عمیق، به خصوص وقتی منابع محدود باشند، غیرکاربردی خواهد بود. در مقاله‌ سریواستاواSrivastava  و همکارانش نیز به این مشکل اشاره شده و راهکاری برای حل مطرح می‌شود.

Dropout

تکنیک dropout را باید در دو مرحله مورد بررسی قرار داد: آموزش و آزمایش.

مرحله‌ آموزش

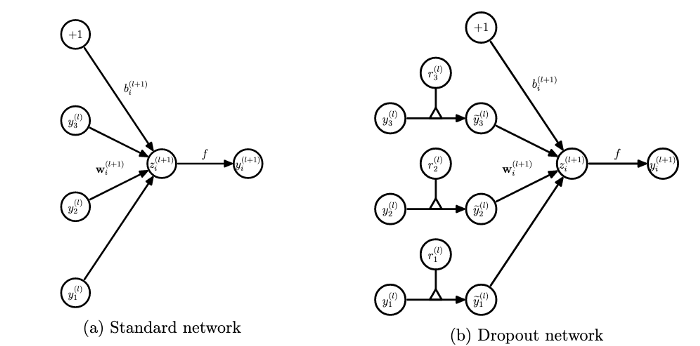
هدف از اجرای dropout در مرحله‌ آموزش ساده است: هنگام آموزش، بعضی از نورون‌ها را خاموش می‌کنیم تا در هر دور، شبکه‌ها با هم تفاوت داشته باشند. تصویر بالا نحوه‌ خاموش کردن نورون‌ها را نشان می‌دهد: هر ورودی y_i را در یک نورون r_i که یک توزیع دونقطه‌ایTwo-point distribution  با خروجی 0 و 1 (با توزیع برنولیBernoulli distribution ) است، ضرب می‌کنیم. بدون اجرای dropout، گذر رو به جلوForward pass  در مرحله‌ آموزشی چنین شکلی خواهد داشت:

در این معادله، ورودی تابع فعالسازیActivation function  (f) در واقع همان حاصل‌ضربِ جمع وزن‌ها (w) در ورودی (y) است. اما بعد از اجرای dropout، گذر رو به جلو بدین شکل خواهد بود:

همانطور که می‌بینید، در خط دوم این معادله یک نورون r به معادله اضافه می‌شود که یا (به احتمال p) با ضرب وزن در 1 آن را نگه می‌دارد یا این‌که (به احتمال 1-p) با ضرب آن در 0 آن را خاموش می‌کند؛ ادامه‌ گذر رو به جلو، مشابه زمانی است که از dropout استفاده نکردیم.

مرحله‌ آزمایش

از آن‌جایی که هر نورونی می‌تواند دو حالت ممکن به خود بگیرد، برای یک شبکه‌ عصبی با n نورون، مرحله‌ آموزش را می‌توان مجموعه‌ای از  شبکه‌ عصبی متفاوت در نظر گرفت. در مرحله‌ آموزش نیز می‌توان از روش‌های میانگین‌گیری مثل مدل گروهی استفاده کنیم؛ بدین طریق که همه‌ شبکه‌های عصبی ممکن استنتاج را انجام می‌دهند و سپس از نتایج آن‌ها، میانگین می‌گیریم. اما این کار امکان‌پذیر نیست و هزینه‌ محاسباتی بالایی دارد. به همین دلیل، سریواستاوا و همکارانش راهکاری برای برآورد میانگین ارائه می‌دهند که بدون نیاز به Dropout، در شبکه‌های عصبی استنتاج انجام می‌دهد.

برای دستیابی به این مقدار برآوردشده، باید اطمینان حاصل کنیم خروجی استنتاج برابر با مقدار موردانتظار استنتاج هنگام آموزش است. فرض کنید خروجی یک نورون z و احتمال Dropout یا p(r) برابر با p است. در این صورت، مقدار موردانتظار نورون با اجرای dropout بدین طریق به دست می‌آید:

بدین ترتیب، برای این‌که خروجی آزمایش با خروجی موردانتظار آموزش برابر باشد، وزن‌های همه‌ نورون‌ها را در مرحله‌ آزمایش بر اساس مقدار p مقیاس‌بندی می‌کنیم. به این روش «استنتاج مقیاس‌بندی وزنWeight scaling inference » گفته می‌شود.

پیاده‌سازی Dropout

در کنفرانس cs23 با موضوع شبکه‌های عصبی، یک پیاده‌سازی بسیار ساده از dropout مطرح شد. در مقاله‌ حاضر، این پیاده‌سازی را مقداری تغییر داده و قسمت‌های مهم آن را با جزئیات توضیح خواهیم داد.

این نسخه پیاده‌سازی dropout مربوط به اجرای آن در یک DNN سه‌لایه‌ای با توابع فعال سازی ReLU است. همانطور که مشاهده می‌کنید، dropout قبل از انتقال ورودی به لایه‌ نهانHidden layer  دوم و لایه‌ خروجی اجرا شده است. توزیع برنولی یک توزیع دوجمله‌ای خاص است که در آن n=1؛ به همین دلیل برای ایجاد ماسک Dropout، می‌توانیم از numpy.random.binomial استفاده کنیم.

اگر دقت کنید می‌بینید که در مرحله‌ پیش‌بینی، همه‌ لایه‌ها را در keep_prob ضرب می‌کنیم. این در واقع اجرای همان روش «استنتاج از طریق مقیاس‌بندی وزن‌ها» است که بالاتر توضیح دادیم. با این حال، اجرای این روش برای همه‌ لایه‌ها، زمان پیش‌بینی را افزایش می‌دهد. به همین دلیل یک نمونه پیاده‌سازی دیگر مطرح شده است که این مشکل را حل می‌کند؛ در این روش که Dropout معکوس خوانده می‌شود، هنگام آموزش، وزن‌ها بر اساس 1/keep_prob مقیاس‌بندی می‌شوند.

نکته‌ دیگر این است که به جای این‌که در مرحله‌ پیش‌بینی، خروجی را بر اساس keep_prob مقیاس‌بندی کنیم، در مرحله‌ آموزش، وزن‌ها را بر اساس 1/keep_prob مقیاس‌بندی می‌کنیم. بدین ترتیب، مقادیر موردانتظار خروجی‌ها به صورت z (نمره‌ی استاندارد) به دست می‌آید و دیگر نیازی به مقیاس‌بندی در مرحله‌ پیش‌بینی نخواهد بود.