
آموزش الگوریتم خوشهبندی K میانگین در پایتون
الگوریتم خوشهبندی K میانگین یکی از انواع یادگیری ماشینی نظارتنشده است که خوشه دادههای درون یک دیتاست را شناسایی میکند. الگوریتمهای خوشهبندی Clustering تنوع زیادی دارند، اما الگوریتم K میانگین یکی از قدیمیترین و در دسترسترین آنها است. این ویژگیها باعث میشوند اجرای الگوریتم K میانگین در پایتون حتی برای برنامهنویسان و دانشمندان داده تازهکار نیز راحت و آسان باشد.
اگر میخواهید بدانید الگوریتم K میانگین برای حل چه مسائلی قابلاستفاده است و چگونه میتوان آن را در پایتون پیادهسازی کرد، در این مقاله آموزشی همراه ما باشید. در این مقاله، مثالی از الگوریتم K میانگین را قدم به قدم از مرحله پیشپردازش دادهها تا ارزیابی نتایج بررسی میکنیم و کد آن را به زبان پایتون مینویسیم.
مواردی که در این بخش از مقاله خواهید آموخت عبارتاند از
- الگوریتم K میانگین چیست؟
- چه زمانی میتوان از الگوریتم K میانگین برای تحلیل دادهها استفاده کرد؟
- چگونه میتوان الگوریتم K میانگین را در پایتون پیادهسازی کرد؟
- چگونه تعداد خوشهها را تعیین کنیم؟
از این لینک میتوانید کد کامل این مقاله آموزشی را بارگیری نموده، مثالها را به ترتیب در آن مشاهده کنید و سپس الگوریتم K میانگین خود را در پایتون پیادهسازی نمایید.
خوشهبندی به چه معناست؟
خوشهبندی در حقیقت مجموعهای از روشهاست که برای تفکیک دادهها در چند گروه یا خوشه مختلف استفاده میشود. خوشهها نیز در واقع گروهی از اشیا Data objects (مجموعهای از دادههای درون دیتاست) هستند که شباهت آنها با دادههای درون آن خوشه بیشتر از دادههای سایر خوشهها است. خوشهبندی به شناسایی دو خصلت معنیداری Meaningfulness و کاربرد Usefulness دادهها به ما کمک میکند.
خوشههای معنادار دانش تخصصی حوزه کاری Domain knowledge شما را گسترش میدهند. برای مثال، محققان در حوزه پزشکی یک الگوریتم خوشهبندی بر روی آزمایشات بیان ژن Gene expression اعمال کردند که توانست بیماران را بر اساس نوع واکنششان به روشهای درمانی در چند گروه مختلف قرار دهد.
از طرفی خوشههای کاربردی در روال پردازشی دادهها نوعی واسطه به حساب میآیند. برای مثال، کسبوکارهای مختلف میتوانند با استفاده از الگوریتمهای خوشهبندی، مشتریان خود را بر اساس تاریخچه خرید در گروههای مختلف قرار دهند و سپس بر مبنای این گروهها کمپینهای تبلیغاتی هدفمند راهاندازی کنند.
خوشهبندی کاربردهای دیگری نیز دارد. برای مثال، میتوان به خوشهبندی اسناد و تحلیل شبکههای اجتماعی اشاره کرد. کاربردهای این الگوریتم فقط محدود به یک یا چند صنعت نیستند و به همین دلیل خوشهبندی برای کسانی که با دادهها سروکار دارند، مهارتی ارزشمند به شمار میآید.
مروری بر روشهای خوشهبندی
انتخاب درست الگوریتم خوشهبندی برای دیتاستها اغلب کار دشواری است، زیرا گزینههای زیادی پیش روی ما قرار دارد. مهمترین عواملی که این تصمیم را تحتتأثیر قرار میدهند عبارتاند از: مشخصات خوشهها، ویژگیهای درون دیتاست، شمار دادههای پرت Outliers و شمار اشیای دادهای.
در ادامه با بررسی محبوبترین الگوریتمهای خوشهبندی از جمله خوشهبندی تفکیکی Partitional Clustering ، خوشهبندی سلسله مراتبی Hierarchical Clustering و o خوشهبندی مبتنی بر چگالی Density-Based Clustering ، خواهیم دید که چطور این عوامل در انتخاب بهترین و مناسبترین رویکرد خوشهبندی به ما کمک میکنند.
خوب است پیش از بررسی الگوریتم K میانگین مروری بر این الگوریتمها داشته باشیم و نقاط قوت و ضعف آنها را ببینیم تا متوجه شویم که چرا الگوریتم K میانگین با بسیاری از الگوریتمهای خوشهبندی سازگار است.
خوشهبندی تفکیکی
در روش خوشهبندی تفکیکی شیءدادهها را به گروههای کاملاً مجزا تقسیم میکنیم. بهعبارت دیگر، هیچ شیئی نمیتواند در بیش از یک خوشه قرار بگیرد و هر خوشه نیز حداقل یک عضو دارد.
در این روش کاربر باید تعداد خوشهها را که همان متغیر k است، مشخص کند. طرز کار بسیاری از الگوریتمهای خوشهبندی به این صورت است که طی فرایندی تکراری، زیرمجموعههایی از نقطه دادهها را به k خوشه تعریفشده تخصیص میدهند. الگوریتم K میانگین و لگوریتم K واسط k-medoids دو نمونه از الگوریتمهای خوشهبندی تفکیکی هستند.
این الگوریتمها غیرقطعی Nondeterministic هستند. منظور از غیرقطعی بودن این است که اگر این الگوریتمها را چندین بار روی یک مجموعه ورودی مشخص اعمال کنیم، ممکن است هر بار نتیجه متفاوتی به دست آید.
نقاط قوت روشهای خوشهبندی تفکیکی:
- این روشها زمانی که خوشهها شکل دایرهای داشته باشند، عملکرد خوبی دارند.
- این روشهای با توجه به میزان پیچیدگی الگوریتم مقیاسبندی میشوند.
نقاط ضعف روشهای خوشهبندی تفکیکی:
- وقتی خوشهها دارای اشکال پیچیده و متفاوت باشند، این روشها عملکرد چندان خوبی ندارند.
- وقتی خوشهها دارای چگالیهای متفاوتی باشند، این روشها با مشکل مواجه میشوند و اجرا نخواهند شد.
خوشهبندی سلسهمراتبی
خوشهبندی سلسلهمراتبی با ساخت یک سلسلهمراتب، دادهها را به خوشههای تعریفشده تخصیص میدهد. این سلسلهمراتب هم میتواند از بالا به پایین باشد و هم از پایین به بالا:
- خوشهبندی تجمیعی Agglomerative clustering : این نوع از خوشهبندی دارای رویکرد پایین به بالا است و هر بار دو نقطه دادهای را که بیشترین شباهت به هم دارند، با هم در یک خوشه قرار میدهد، تا نهایتاً تمام دادهها در یک خوشه واحد قرار بگیرند.
- خوشهبندی تقسیمی Divisive clustering : این نوع از خوشهبندی دارای رویکرد بالا به پایین است. در این رویکرد ابتدا همه نقطهدادهها در یک خوشه قرار میگیرند و سپس هر بار خوشهای را که کمترین شباهت با سایرین دارد، از خوشه جدا میکند، تا در نهایت فقط یک نقطه داده باقی بماند.
این روشها یک سلسلهمراتب درختی از نقطه دادهها ایجاد میکنند که به آن دندروگرام Dendrogram گفته میشود. در روش خوشهبندی سلسلهمراتبی نیز دقیقاً مثل روش تفکیکی، تعداد خوشهها (k) از قبل از سوی کاربر تعیین میشود. سپس با تخصیص خوشهها، دندروگرام، تا عمق مشخصی که منتهی به ایجاد k گروه از دندروگرامهای کوچکتر شود، تقسیم میشود.
خوشهبندی سلسلهمراتبی برخلاف اکثر روشهای خوشهبندی تفکیکی که غیرقطعی هستند، نتایج قطعی به دست میدهد. منظور از قطعی بودن نتایج این است که اگر الگوریتم را چندین بار روی ورودیهای یکسان اجرا کنیم، خوشههای خروجی تغییری نخواهند کرد.
نقاط قوت روشهای خوشهبندی سلسلهمراتبی
- این روشها اغلب اطلاعات دقیقی از روابط میان شیءدادهها به ما میدهند.
- همچنین دندروگرام و خروجی آنها قابل تفسیر است.
نقاط ضعف روشهای خوشهبندی سلسلهمراتبی
- در این روشها هزینه محاسبات بالاست و هر چه پیچیدگی الگوریتم بیشتر باشد این هزینه نیز بیشتر میشود.
- این روشها نسبت به نویزها یا اختلالات و دادههای پرت حساس هستند.
خوشهبندی مبتنی بر چگالی
خوشهبندی مبتنی بر چگالی، تخصیص دادهها به خوشهها را بر اساس چگالی نقطه دادهها در یک منطقه انجام میدهد. خوشهها در منطقهای قرار میگیرند که چگالی نقطهدادهها زیاد باشد و اطراف آنها مناطقی باشد که چگالی نقطهدادهها کم است.
برخلاف سایر روشهای خوشهبندی در این رویکرد لازم نیست کاربر تعداد خوشهها را تعیین کند. در عوض، یک پارامتر مبتنی بر فاصله Distance-based parameter در این قبیل الگوریتمها وجود دارد که بهعنوان یک حد آستانه Threshold قابل تنظیم عمل میکند و تعیین میکند که حداکثر فاصله نقاطی که میتوانند در یک خوشه قرار بگیرند باید چقدر باشد.
الگوریتمهای DBSCAN و OPTICS از نمونههای الگوریتمهای خوشهبندی مبتنی بر چگالی هستند.
نقاط قوت روشهای خوشهبندی مبتنی بر چگالی
- این روشها در تشخیص خوشههای غیر دایرهای عملکرد خوبی دارند.
- در برابر دادههای پرت نیز مقاوم هستند.
نقاط ضعف روشهای خوشهبندی مبتنی بر چگالی
- این روشها برای خوشهبندی در فضاهایی با ابعاد بالا چندان مناسب نیستند.
- این روشها در تشخیص خوشههای دارای چگالی متفاوت، عملکرد خوبی ندارند.
چگونه الگوریتم خوشهبندی K میانگین را در پایتون اجرا کنیم؟
در این بخش، نسخه متداول الگوریتم خوشهبندی K میانگین را قدمبهقدم بررسی میکنیم. درک جزئیات این الگوریتم قدم مهمی در فرایند نوشتن کدها و روال پردازشی آن در پایتون است. نکاتی که در این بخش خواهید آموخت به شما کمک میکنند، تا تشخیص دهید آیا الگوریتم خوشهبندی K میانگین انتخاب درستی برای حل مسئله مدنظرتان است یا خیر.
مفهوم الگوریتم خوشهبندی K میانگین
پیادهسازی الگوریتم خوشهبندی K میانگین بسیار ساده است. در قدم اول باید k تا مقدار تصادفی بهعنوان نقاط مرکزی (این k برابر با تعداد خوشههای مدنظرمان است) انتخاب کنید. نقاط مرکزی Centroids ، در واقع نقطه دادههایی هستند که در مرکز خوشه قرار میگیرند.
قسمت اصلی این الگوریتم در حقیقت یک فرایند دو مرحلهای به نام امید ریاضی- بیشینهسازی expectation-maximization است. در مرحله امید ریاضی هر نقطهداده به نزدیکترین نقطه مرکزی تخصیص داده میشود. سپس در مرحله بیشینهسازی میانگین همه نقاط درون خوشهها محاسبه شده و یک نقطه مرکزی جدید برای هر یک به دست آید. در زیر شکل متداول الگوریتم خوشهبندی K میانگین را مشاهده میکنید:

کیفیت فرایند تخصیص خوشه پس از همگرا شدن Converge نقاط مرکزی یا بهعبارتی منطبق شدن بر تخصیص پیشین، به مجموع مربعات خطا Sum of the squared error [22] (SSE) بستگی دارد. طبق تعریف، SSE مجموع مربعات فاصله اقلیدسی Euclidean distances هر نقطه از نزدیکترین نقطه مرکزی است. از آنجا که محاسبه SSE در واقع برآورد خطا است، هدف الگوریتم خوشهبندی K میانگین حداقل کردن مقدار آن است.
برای مثال، ما الگوریتم K میانگین را دو بار بهصورت مجزا اجرا کردیم و هر بار 5 تکرار داشتیم. در نمودار زیر نقاط مرکزی و نحوه بهروزرسانی شدن SSE را در این فرایند مشاهده میکنید.
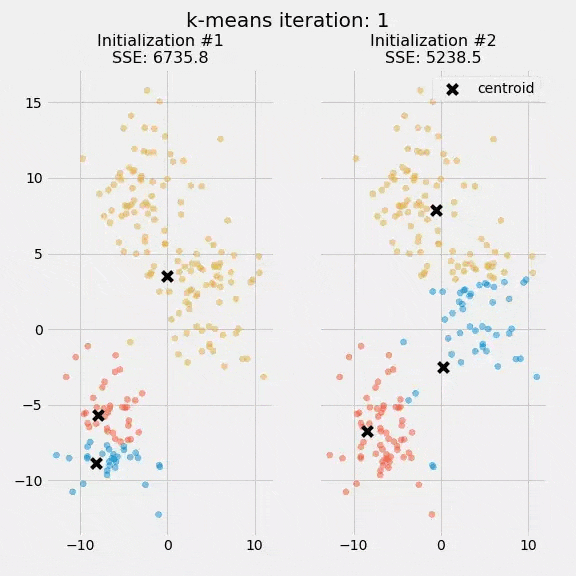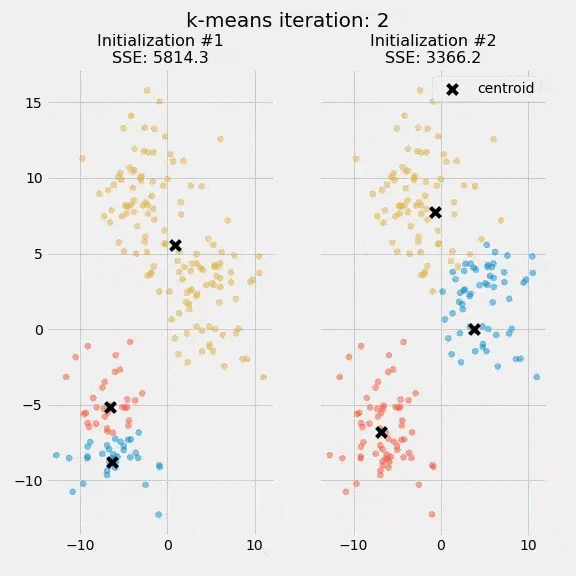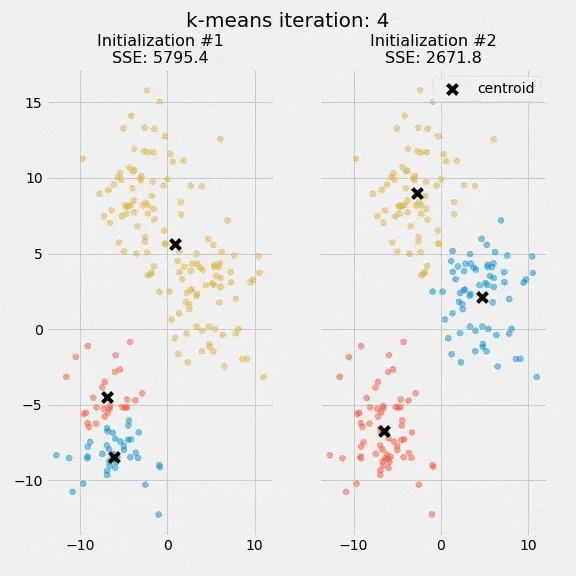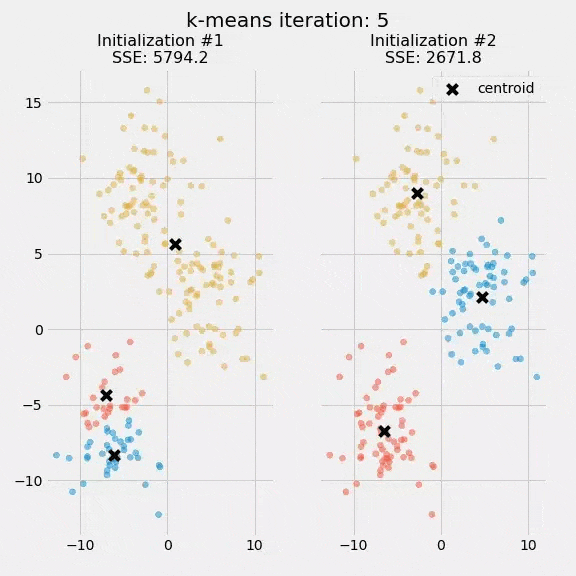
هدف از ترسیم این نمودار این بود که نشان دهیم مقداردهی اولیه Initialization نقاط مرکزی از اهمیت زیادی برخوردار است. همچنین در این نمودار میتوان کاربرد SSE بهعنوان معیار سنجش عملکرد الگوریتم خوشهبندی را به چشم دید. پس از انتخاب تعداد خوشهها و مقداردهی نقاط مرکزی، فرایند امید ریاضی- بیشینهسازی تکرار میشود، تا نقاط مرکزی به همگرایی برسند و در جای خود ثابت بمانند.
تصادفی بودن مرحله مقداردهی اولیه باعث میشود نتیجه الگوریتم K میانگین قطعی نباشد و با هر بار اجرای الگوریتم روی دیتاست مشخص، نحوه تخصیص خوشههای تغییر کند. محققان معمولاً الگوریتم K میانگین را چندین بار و با مقدارهای اولیه متفاوت اجرا میکنند و سپس تخصیص خوشهای را انتخاب میکنند که SSE آن حداقل باشد.
نوشتن اولین الگوریتم خوشهبندی K میانگین
خوشبختانه، الگوریتم K میانگین در پکیج محبوب scikit-learn بهخوبی پیادهسازی شده است. در ادامه خواهیم آموخت که چگونه نسخه scikit-learn الگوریتم K میانگین را اجرا و پیادهسازی کنیم.
برای نوشتن و اجرای کدی که در این مقاله آن را بررسی میکنیم، به چندین پکیج دیگر نیز نیاز داریم. به علاوه، من فرض را بر این میگذارم که پایتون را از طریق Anaconda نصب کردهاید. برای کسب اطلاعات بیشتر در خصوص نحوه راهاندازی محیطهای پایتونی لازم برای اجرای الگوریتمهای یادگیری ماشینی در سیستم عامل ویندوز به این لینک مراجعه فرمایید.
بسیارخب، حال میتوانیم مرحله کدنویسی را با نصب پکیجهای موردنیاز آغاز کنیم:
(base) $ conda install matplotlib numpy pandas seaborn scikit-learn ipython
(base) $ conda install -c conda-forge kneed
کد کامل این مثال قابل دانلود است و میتوانید آن را مرحلهبهمرحله در بخش کنسول نرمافزارipython یا Jupyter Notebook اجرا کنید. کدها را میتوانید از این لینک بارگیری نمایید.
در این مرحله باید ماژولهای موردنیاز برای این بخش را وارد محیط برنامهنویسی خود کنیم:
import matplotlib.pyplot as plt
from kneed import KneeLocator
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
from sklearn.preprocessing import StandardScaler
نموداری که در بالا مشاهده کردید، یک فایل با فرمت GIF بود که میتوانید با استفاده از یکی از توابع ساده scikit-learn به نام make_blobs() دادههایی مشابه آن تولید کنید. تابع make_blobs() بهمنظور ایجاد خوشهها یا دادههای غیرواقعی استفاده میشود. پارامترهایی که در این تابع تعریف میشوند به ترتیب زیر هستند:
• n_samples: این پارامتر تعداد کل نمونههایی را که باید تولید شوند، را تعیین میکند.
• Centers: این پارامتر تعداد نقاط مرکزی را که باید تولید شوند را، مشخص میکند.
• cluster_std: این پارامتر مقدار انحراف از معیار است.
تابع make_blobs() یک تاپل Tuple
بهعنوان خروجی به ما میدهد که حاوی دو مقدار است:
- یک آرایه NumPy دو بعدی حاوی مقادیر x و y هر یک از نمونهها
- یک آرایه NumPy تک بعدی حاوی برچسب خوشهها
تولید دادهها و برچسبهای غیرواقعی بهصورت زیر انجام میشود:
features, true_labels = make_blobs(
n_samples=200,
centers=3,
cluster_std=2.75,
random_state=42
)
تولید و نوشتن مجدد الگوریتمهای یادگیری ماشینی غیرقطعی مثل الگوریتم K میانگین کار سختی است. باید به پارامتر random_state یک مقدار عددی، صحیح و مشخص داد، تا دادههایی که در این مقاله نمایش داده میشوند با دادههای تولیدشده برای شما یکسان باشند؛ اما بهطور کلی بهتر است مقداری برای پارامتر random_state تعریف نشود و مقدار آن همان مقدار پیشفرض (که None است) باقی بماند.
با نوشتن کد زیر میتوانید پنج عنصر اول هر یک از متغیرهایی را که از طریق make_blobs() تولید شدند، مشاهده کنید.
In [3]: features[:5]
Out[3]:
array([[ 9.77075874, 3.27621022],
[ -9.71349666, 11.27451802],
[ -6.91330582, -9.34755911],
[-10.86185913, -10.75063497],
[ -8.50038027, -4.54370383]])
In [4]: true_labels[:5]
Out[4]: array([1, 0, 2, 2, 2])
ممکن است واحد اندازهگیری دادههای عددی موجود در یک دیتاست با هم متفاوت باشد. برای مثال، واحد اندازهگیری قد اینچ Inches و واحد اندازهگیری وزن، پوند Pounds است؛ اما الگوریتمهای یادگیری ماشینی بین قد و وزن برای متغیر وزن اهمیت بیشتری قائل میشوند، چون مقادیر عددی آن متمایز و بزرگتر از مقادیر عددی متغیر قد هستند؛ اما ما میخواهیم الگوریتمهای یادگیری ماشینی ارزش یکسانی برای تمامی متغیرها قائل شوند. به همین دلیل، لازم است تمامی ویژگیها (یا متغیرها) از نظر واحد اندازهگیری یکسانسازی شوند.
فرایند تبدیل واحد ویژگیهای عددی و یکسانسازی مقیاس آنها، مقیاسبندی ویژگی Feature scaling نامیده میشود. وقتی با الگوریتمهای یادگیری ماشینی مبتنی بر فاصله سروکار دارید، این کار مرحله مهمی از فرایند پیشپردازش دادهها است و تأثیر بسزایی بر عملکرد الگوریتم شما خواهد داشت.
روشهای زیادی برای مقیاسبندی ویژگیها وجود دارد. برای تشخیص روش مناسب مقیاسبندی دیتاست بخش پیشپردازش از راهنمای جامع کتابخانه scikit-learn را مطالعه کنید.
در این مثال، از کلاس StandardScaler استفاده خواهیم کرد که نوعی فرایند مقیاسبندی به نام استانداردسازی Standardization
را روی دیتاست پیادهسازی میکند. در این روش مقادیر ویژگیهای عددی دیتاست مقیاسبندی میشوند و بهنحوی تغییر میکنند که میانگین آنها برابر صفر و انحراف از معیار برابر 1 شود.
scaler = StandardScaler()
scaled_features = scaler.fit_transform(features)
بیایید ببینیم مقادیر ذخیرهشده در متغیر scaled_features چگونه مقیاسبندی شدهاند.
In [6]: scaled_features[:5]
Out[6]:
array([[ 2.13082109, 0.25604351],
[-1.52698523, 1.41036744],
[-1.00130152, -1.56583175],
[-1.74256891, -1.76832509],
[-1.29924521, -0.87253446]])
حال دادهها آماده خوشهبندی شدن هستند. میتوانیم در کلاس برآوردگر Estimator class
KMeans از کتابخانه scikit-learn پارامترهای الگوریتم را به دلخواه خود مقداردهی کنیم و سپس این برآوردگر را روی دادهها برازش دهیم. الگوریتم پیادهسازیشده در کتابخانه scikit-learn کاملاً انطعافپذیر است و میتوان پارامترهای آن را به دلخواه تنظیم کرد.
پارامترهای استفادهشده در این مثال به ترتیب زیرند:
init: این پارامتر مربوط به مقداردهی اولیه است. در نسخه استاندارد الگوریتم K میانگین مقدار پارامترinitبرابرrandomاست. اما اگر آن را برابرk-means++قرار دهیم، همگرایی تسریع میشود.n_clustersn_initmax_iter: این پارامتر تعداد دفعات تکرار هر مقداردهی در الگوریتم K میانگین را مشخص میکند.
با استفاده از آرگومانهای زیر میتوانید یک نمونه از کلاس KMeans ایجاد کنید:
kmeans = KMeans(
init="random",
n_clusters=3,
n_init=10,
max_iter=300,
random_state=42)
اسامی پارامترهای استفادهشده در این کد دقیقاً مطابق همان چیزی است که در این مقاله گفته شد. حال که کلاس KMeans را تعریف کردیم، زمان آن است که آن را روی دادههای ذخیرهشده در متغیر scaled_features برازش دهیم. این کلاس الگوریتم را 10 بار اجرا میکند و در هر بار نیز حداکثر 300 تکرار انجام میگیرد.
In [8]: kmeans.fit(scaled_features)
Out[8]:
KMeans(init='random', n_clusters=3, random_state=42)
پس از فراخوانی.fit() میتوانید در خصوص مقداردهی که منجر به کمترین SSE شده، اطلاعات به دست آورید.
In [9]: # The lowest SSE value
...: kmeans.inertia_
Out[9]: 74.57960106819854
In [10]: # Final locations of the centroid
...: kmeans.cluster_centers_
Out[10]:
array([[ 1.19539276, 0.13158148],
[-0.25813925, 1.05589975],
[-0.91941183, -1.18551732]])
In [11]: # The number of iterations required to converge
...: kmeans.n_iter_
Out[11]: 6
در نهایت، خوشهبندیهای انجامشده بهصورت یک آرایه NumPy تکبعدی در متغیری به نام kmeans.labels_ ذخیره میشوند.
In [12]: kmeans.labels_[:5]
Out[12]: array([0, 1, 2, 2, 2], dtype=int32)
باید به این نکته دقت داشته باشید که برچسب خوشهها برای دو شیءداده ابتدایی برعکس است. یعنی در حقیقت و در true_labels داریم [1, 0]، اما در kmeans.labels_ برچسبها به این صورت [0, 1] هستند. البته خوشههای این دو شیءداده در kmeans.labels_ تغییری نمیکند و همان جایی هستند که باید باشند.
این اتفاق بسیار معمول است، چراکه ترتیب برچسب خوشهها به مقداردهی اولیه بستگی دارد. یعنی در دومین اجرا ممکن است خوشهای که در اولین اجرا شماره صفر را داشته، تبدیل شود به خوشه 1 یا برعکس. در هر حال، این مسئله معیارهای ارزیابی خوشهبندی Clustering evaluation metrics را تحتتأثیر قرار نمیدهد.
انتخاب تعداد خوشهها
در این بخش نگاهی خواهیم داشت به 2 روش پرکاربرد برای تعیین تعداد خوشههای مناسب برای هر مسئله.
- روش elbow
- روش silhouette
این دو روش اصولاً مکمل هم هستند نه جایگزین. برای اجرای روش elbow باید k-means را چندین بار اجرا کنیم بهطوری که هر بار k یک واحد اضافه شود و SSE را در هر تکرار ثبت کنیم:
In [13]: kmeans_kwargs = {
...: "init": "random",
...: "n_init": 10,
...: "max_iter": 300,
...: "random_state": 42,
...: }
...:
...: # A list holds the SSE values for each k
...: sse = []
...: for k in range(1, 11):
...: kmeans = KMeans(n_clusters=k, **kmeans_kwargs)
...: kmeans.fit(scaled_features)
...: sse.append(kmeans.inertia_)
در کد بالا از عملگر جداساز Unpacking در دیکشنریهای پایتون (که بهصورت ** نمایش داده میشود) استفاده کردیم. برای مطالعه بیشتر در خصوص این عملگر قدرتمند، به این مقاله مراجعه نمایید.
اگر نمودارSSE و تعداد خوشهها را رسم کنید، میبینید که با افزایش تعداد خوشهها، SSE کاهش مییابد؛ زیرا هر چه تعداد نقاط مرکزی افزایش یابد، فاصله هر نقطهداده تا نزدیکترین نقطه مرکزی کاهش خواهد یافت.
در این نمودار یک نقطه مشخص وجود دارد که سرعت کاهش SSE از آن به بعد تغییر میکند. به این نقطه elbow میگوییم. مقدار x این نقطه نوعی موازنه منطقی بین مقدار خطا و تعداد خوشهها در نظر گرفته میشود. در مثال ما elbow در نقطه x=3 قرار دارد:
plt.style.use("fivethirtyeight")
plt.plot(range(1, 11), sse)
plt.xticks(range(1, 11))
plt.xlabel("Number of Clusters")
plt.ylabel("SSE")
plt.show()کد بالا نمودار زیر را برای ما ترسیم میکند:
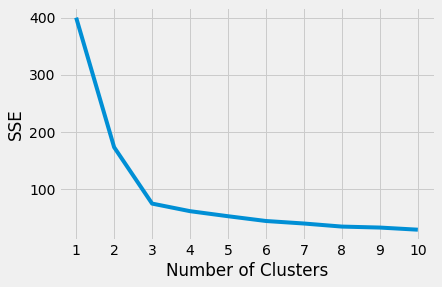
البته تعیین نقطه elbow در منحنی همیشه به این سادگی نیست. اگر در تعیین موقعیت این نقطه به مشکل برخوردید، میتوانید از پکیج kneed استفاده کنید و با نوشتن کد، نقطهelbow را به دست آورید:
kl = KneeLocator(
range(1, 11), sse, curve="convex", direction="decreasing"
)
kl.elbow
ضریب silhouette در واقع برآوردی است از میزان جامعیت و تفکیک خوشهها. این ضریب بر اساس دو معیار زیر به ما میگوید که خوشه نسبت دادهشده به هر نقطهداده، تا چه حد درست و مناسب است.
- فاصله نقطهداده مدنظر از سایر نقاط درون خوشه
- فاصله نقطهداده مدنظر از نقاط درون سایر خوشهها
مقدار ضریب silhouette عددی است بین 1- و 1. هرچه مقدار این ضریب بیشتر باشد، حاکی از آن است که نمونهها به خوشه خودشان نزدیکترند، تا سایر خوشهها.
در scikit-learn، میانگین ضریب silhouette تمامی نمونهها محاسبه و در قالب یک عدد واحد نمایش داده میشود. تابع silhouette score() حداقل به دو خوشه نیاز دارد، در غیر این صورت با خطا مواجه خواهد شد.
حال مجدداً روی مقادیر k حلقه میزنیم و اینبار به جای محاسبه SSE، ضریب silhouette را محاسبه میکنیم:
# A list holds the silhouette coefficients for each k
silhouette_coefficients = []
# Notice you start at 2 clusters for silhouette coefficient
for k in range(2, 11):
kmeans = KMeans(n_clusters=k, **kmeans_kwargs)
kmeans.fit(scaled_features)
score = silhouette_score(scaled_features, kmeans.labels_)
silhouette_coefficients.append(score)
با رسم نمودار میانگین امتیاز silhouette برای هر k متوجه خواهیم شد که بهترین مقدار برای k، مقدار 3 است، زیرا این مقدار بیشترین امتیاز را کسب کرده است:
plt.style.use("fivethirtyeight")
plt.plot(range(2, 11), silhouette_coefficients)
plt.xticks(range(2, 11))
plt.xlabel("Number of Clusters")
plt.ylabel("Silhouette Coefficient")
plt.show()
کد بالا نمودار زیر را برای ما رسم خواهد کرد:
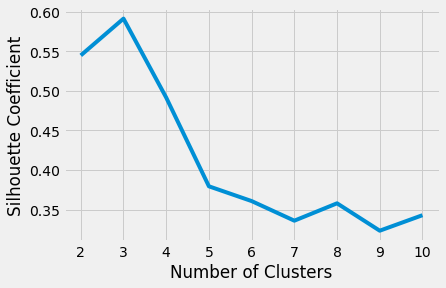
البته در تصمیمگیری نهایی برای تعداد خوشههایی که باید در نظر گرفته شوند، باید علاوه بر معیارهای ارزیابی خوشهبندی، دانش حوزه تخصصی خود را نیز مدنظر قرار دهید.
ارزیابی عملکرد الگوریتم خوشهبندی با روشهای پیشرفته
روشelbow و ضریب silhouette عملکرد الگوریتم خوشهبندی را بدون درنظر گرفتن برچسبهای واقعی Ground truth labels ارزیابی میکنند. برچسبهای واقعی، نقطهدادهها را در گروههایی که از سوی یک انسان یا الگوریتم دیگر تخصیص داده شدهاند، قرار میدهند. این معیارها سعی میکنند، تا تعداد درست خوشهها را به شما پیشنهاد کنند، اما وقتی بدون در نظر گرفتن سایر عوامل محیطی به آنها اعتماد کنید، ممکن است شما را به اشتباه بیندازند. باید این نکته را یادآوری کنم که در عمل، دیتاستهای کمی دارای برچسبهای واقعی هستند.
وقتی عملکرد الگوریتم میانگین k در مسائل خوشهبندی غیر کروی را با روشهای مبتنی بر چگالی مقایسه کنیم، متوجه میشویم که نتایج حاصل از روش elbow و ضریب silhouette بهندرت با منطق انسان جور در میآید. این مسئله برای ما روشن میسازد که چرا باید از روشهای پیشرفتهتری برای ارزیابی عملکرد الگوریتم خوشهبندی استفاده کنیم. برای بررسی یک مثال در این زمینه باید چند ماژول دیگر را به محیط برنامهنویسی خود وارد کنیم:
from sklearn.cluster import DBSCAN
from sklearn.datasets import make_moons
from sklearn.metrics import adjusted_rand_score
این بار از make_moons() استفاده میکنیم، تا دادههایی غیرواقعی با شکل حلال ماه تولید کنیم:
features, true_labels = make_moons(
n_samples=250, noise=0.05, random_state=42
)
scaled_features = scaler.fit_transform(features)
حال دو الگوریتم میانگین k و DBSCAN را روی این دادههای جدید برازش میدهیم و عملکرد آنها را با رسم نمودار تخصیص خوشه، ارزیابی کنیم. برای رسم نمودارها از کتابخانه Matplotlib استفاده میکنیم:
# Instantiate k-means and dbscan algorithms
kmeans = KMeans(n_clusters=2)
dbscan = DBSCAN(eps=0.3)
# Fit the algorithms to the features
kmeans.fit(scaled_features)
dbscan.fit(scaled_features)
# Compute the silhouette scores for each algorithm
kmeans_silhouette = silhouette_score(
scaled_features, kmeans.labels_
).round(2)
dbscan_silhouette = silhouette_score(
scaled_features, dbscan.labels_
).round (2)
برای دیدن مقدار ضریب silhouette برای هر دو الگوریتم کافی است به شیوه زیر عمل کنید، تا بتوانید آنها را با هم مقایسه نمایید. بهطور کلی، هر چه مقدار ضریب silhouette بزرگتر باشد، خوشهها باکیفیتتر هستند؛ اما مقادیری که در این سناریو به دست میآیند، گمراهکننده هستند:
In [22]: kmeans_silhouette
Out[22]: 0.5
In [23]: dbscan_silhouette
Out[23]: 0.38
همانطور که ملاحظه میفرمایید، ضریب silhouette الگوریتم k میانگین بزرگتر از الگوریتم DBSCAN است. اما چنانکه در نمودار زیر مشاهده میکنید، خوشههایی که الگوریتم DBSCAN پیدا کرده، طبیعیتر هستند و شباهت بیشتری به شکل اصلی دادهها (حلال ماه) دارند:
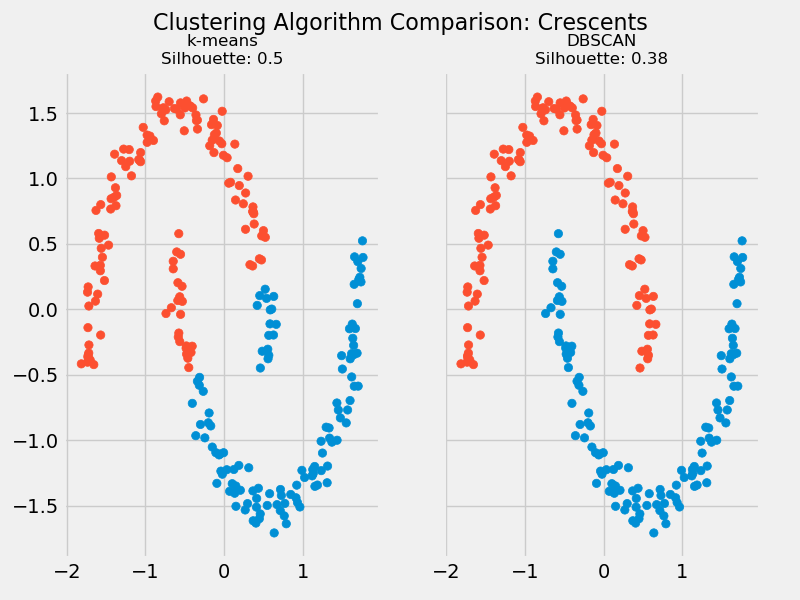
بنابراین در مییابیم که برای مقایسه عملکرد این دو الگوریتم خوشهبندی باید از روش دیگری استفاده کنیم.
در زیر میتوانید کد مربوط به نمودار بالا را مشاهده کنید:
# Plot the data and cluster silhouette comparison
fig, (ax1, ax2) = plt.subplots(
1, 2, figsize=(8, 6), sharex=True, sharey=True
)
fig.suptitle(f"Clustering Algorithm Comparison: Crescents", fontsize=16)
fte_colors = {
0: "#008fd5",
1: "#fc4f30",
}
# The k-means plot
km_colors = [fte_colors[label] for label in kmeans.labels_]
ax1.scatter(scaled_features[:, 0], scaled_features[:, 1], c=km_colors)
ax1.set_title(
f"k-means\nSilhouette: {kmeans_silhouette}", fontdict={"fontsize": 12}
)
# The dbscan plot
db_colors = [fte_colors[label] for label in dbscan.labels_]
ax2.scatter(scaled_features[:, 0], scaled_features[:, 1], c=db_colors)
ax2.set_title(
f"DBSCAN\nSilhouette: {dbscan_silhouette}", fontdict={"fontsize": 12}
)
plt.show()
از آنجا که پیش از مدلسازی، برچسبهای واقعی را داریم، برای ارزیابی نمیتوان از روشی استفاده کرد که برچسبها را در فرایند ارزیابی لحاظ میکند؛ اما میتوانیم از معیار رایجی به نام ARI یا شاخص رند تعدیلشده Adjusted rand index (ARI) که در کتابخانه scikit-learn پیادهسازی شده، استفاده کنیم. شاخص ARI برخلاف ضریب silhouette، به کمک خوشههای واقعی، میزان شباهت بین برچسبهای واقعی و پیشبینیشده را میسنجند.
در کد زیر نتیجه ارزیابی عملکرد دو الگوریتم میانگین k و DBSCAN از طریق ARI را مشاهده میکنید:
In [25]: ari_kmeans = adjusted_rand_score(true_labels, kmeans.labels_)
...: ari_dbscan = adjusted_rand_score(true_labels, dbscan.labels_)
In [26]: round(ari_kmeans, 2)
Out[26]: 0.47
In [27]: round(ari_dbscan, 2)
Out[27]: 1.0
مقدار ARI نیز همواره عددی بین 1- و 1 است. در این معیار، وقتی امتیاز الگوریتم به صفر نزدیکتر باشد، به این معناست که تخصیص دادهها به خوشهها بهصورت تصادفی انجام شده است و اگر امتیاز الگوریتمی برابر 1 شود، حاکی از این است که خوشهها بدون هیچ خطایی برچسبگذاری شدهاند.
بر اساس خروجیهای بالا، میتوان گفت که نتیجهگیری ضریب silhouette اشتباه و گمراهکننده بوده است، چراکه بر اساس شاخص ARI، الگوریتم DBSCAN در مقایسه با میانگین k گزینه بهتری برای خوشهبندی دادههای ما در این مثال است.
معیارهای متعددی برای ارزیابی کیفیت و عملکرد الگوریتمهای خوشهبندی وجود دارد که با مراجعه به این لینک میتوانید از جزئیات آنها مطلع شده و معیار ارزیابی مناسب برگزینید.
چگونه در پایتون یک روال پردازشی برای الگوریتم خوشهبندی K میانگین ایجاد کنیم؟
حال که به درکی نسبی از الگوریتم خوشهبندی میانگین k رسیدید، وقت آن است که این الگوریتم را روی یک دیتاست واقعی پیاده کنیم. دیتاست استفاده شده در این مقاله حاوی دادههای مربوط به بیان ژن است که از نسخه خطی نوشتهشده از سوی محققین پروژه The Cancer Genome Atlas تهیه شده است.
در این دیتاست 881 نمونه یا سطر وجود دارد که به یکی از 5 نوع سرطان ذکرشده در این دیتاست تعلق دارند. برای هر نمونه مقادیر بیان ژنِ 20.531 ژن (در ستونها) تعریف شده است. این دیتاست را میتوانید از این لینک بارگیری نمایید یا میتوانید به کمک کد پایتونی زیر آن را استخراج کنید.
کد این پروژه را نیز میتوانید از این لینک دانلود کرده و قدمبهقدم با من پیش بیایید. در این بخش، روال پردازشی قدرتمندی برای الگوریتم خوشهبندی میانگین k طراحی میکنیم. از آنجا که طی این فرایند، دادههای اصلی را بارها تبدیلTransformation خواهیم کرد، روال پردازشی نهایی را میتوان بعدها بهعنوان یک چارچوب کاری کاربردی برای خوشهبندی نیز استفاده کرد.
ساخت روال پردازشی Pipeline Pipeline الگوریتم خوشهبندی K میانگین
فرض کنید میخواهید یک فضای نام tar.close جدید ایجاد کنید. برای ساخت یک روال پردازشی ابتدا باید تمامی ماژولهای موردنیاز از قبیل pandas و seaborn را وارد محیط کنیم:
import tarfile
import urllib
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
from sklearn.cluster import KMeans
from sklearn.decomposition import PCA
from sklearn.metrics import silhouette_score, adjusted_rand_score
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import LabelEncoder, MinMaxScaler
حالا باید دیتاست TCGA را بارگیری کرده و از UCI استخراج نمایید:
uci_tcga_url = "https://archive.ics.uci.edu/ml/machine-learning-databases/00401/"
archive_name = "TCGA-PANCAN-HiSeq-801x20531.tar.gz"
# Build the url
full_download_url = urllib.parse.urljoin(uci_tcga_url, archive_name)
# Download the file
r = urllib.request.urlretrieve (full_download_url, archive_name)
# Extract the data from the archive
tar = tarfile.open(archive_name, "r:gz")
tar.extractall()
tar.close()
پس از آنکه فرایند بارگیری و استخراج کامل شد، باید مسیری مشابه زیر را در محیط خود مشاهده کنید:
TCGA-PANCAN-HiSeq-801x20531/
|
├── data.csv
└── labels.csv
کلاس KMeans در scikit-learn یک آرایه NumPy را بهعنوان آرگومان دریافت میکند. پکیج NumPy تابعی کمکی دارد که با استفاده از آن میتوان فایلهای متنی را در قالب آرایه در حافظه بارگذاری کرد:
datafile = "TCGA-PANCAN-HiSeq-801x20531/data.csv"
labels_file = "TCGA-PANCAN-HiSeq-801x20531/labels.csv"
data = np.genfromtxt(
datafile,
delimiter=",",
usecols=range(1, 20532),
skip_header=1
)
true_label_names = np.genfromtxt(
labels_file,
delimiter=",",
usecols=(1,),
skip_header=1,
dtype="str"
)
حال میخواهیم 3 ستون ابتدایی 5 نمونه اول دیتاست و برچسبهای آنها را ببینیم:
data[:5, :3]
true_label_names[:5]
متغیرdata حاوی تمامی مقادیر بیان ژن 20.531 ژن موجود در دیتاست است. متغیر true_label_names نیز انواع سرطانهایی است که به این 881 نمونه نسبت داده شدهاند. اولین سطر در متغیر data با اولین برچسب در متغیر true_label_names متناظر است.
برچسبها در حقیقت دادههای رشتهای هستند که اسامی خلاصهشده انواع سرطانها را نشان میدهند:
- BRCA : سرطان مهاجم سینه
- COAD : سرطان روده بزرگ
- KIRC : سرطان سلولهای کلیوی
- LUAD : سرطان ریه
- PRAD : سرطان پروستات
برای استفاده از این برچسبها در روشهای ارزیابی باید ابتدا این اسامی خلاصهشده را به کمک LabelEncoder به عدد صحیح یا int تبدیل کنیم:
label_encoder = LabelEncoder()
true_labels = label_encoder.fit_transform(true_label_names)
true_labels[:5]
پس از برازش label_encoder بر روی دادهها میتوانید با استفاده از .classes_ دستههای منحصربهفرد را مشاهده کنید. همچنین بهتر است طول این آرایه را در متغیری مثل n_clusters ذخیره کنید، تا بتوان بعداً نیز از آن استفاده کرد.
label_encoder.classes_
n_clusters = len(label_encoder.classes_)
در روالهای پردازشی کاربردی یادگیری ماشینی، دادهها معمولاً پیش از آن که به الگوریتم خوشهبندی داده شوند، چندین بار تبدیل میشوند. پیش از این اهمیت یکی از روشهای تبدیل یعنی مقیاسبندی ویژگیها را متوجه شدید. یکی دیگر از تکنیکهای تبدیل مهم تقلیل ابعاد Dimensionality reduction است که هدف از آن کاهش تعداد ویژگیهای دیتاست است و این کار با حذف کردن یا ادغام کردن ویژگیها انجام میشود.
تکنیکهای تقلیل ابعاد به ما کمک میکنند، تا مشکلی به نام « نفرین ابعاد the curse of dimensionality » را که در الگوریتمهای یادگیری ماشینی رایج است، رفع کنیم. بهطور خلاصه، وقتی تعداد ویژگیها افزایش یابد، پراکندگی فضای ویژگی Feature space نیز بیشتر میشود. این امر موجب میشود، تا در فضاهایی با ابعاد بالا، پیدا کردن شیءدادههای نزدیک به هم برای الگوریتمها دشوار باشد. از آنجا که دیتاست بیان ژن دارای 20.000 ویژگی است، برای تقلیل ابعاد کاملاً واجد شرایط است.
تحلیل مؤلفه اساسی Principal Component Analysis (PCA) یا PCA یکی از تکنیکهای تقلیل ابعاد است که با نگاشت دادههای ورودی روی تعداد کمتری از ابعاد (که مؤلفه Components نامیده میشوند)، آنها را تبدیل میکند. این مؤلفهها پراکندگی دادههای ورودی را به وسیله یک ترکیب خطی از ویژگیهای آنها ثبت میکند.
نکته: توضیح کامل روش PCA خارج از مبحث این مقاله آموزشی است، اما برای کسب اطلاعات بیشتر در این خصوص میتوانید به این لینک مراجعه نمایید.
قطعه کد بعدی شما را با مفهوم روال پردازشی در scikit-learn آشنا میسازد. کلاس Pipeline در scikit-learn در واقع بهنوعی همان روال پردازشی یادگیری ماشینی است.
فرمت دیتاست بیان ژن برای کلاس KMeans بهینهسازی نشده است و به همین دلیل باید یک روال پردازشی برای پیشپردازش ایجاد کنید. این روال پردازشی یک روش مقیاسبندی ویژگی دیگر به نام MinMaxScaler را جایگزین StandardScaler میکند. این روش زمانی کاربرد دارد که فرض نرمال بودن توزیع همه ویژگی را کنار میگذارید.
قدم بعدی در فرایند ایجاد روال پردازشی برای پیشپردازش، پیادهسازی یک کلاس PCA بهمنظور انجام عمل کاهش ابعاد است.
preprocessor = Pipeline(
[
("scaler", MinMaxScaler()),
("pca", PCA(n_components=2, random_state=42)),
]
)
حال که روال پردازشی دادهها آماده است، باید یک روال پردازشی جداگانه نیز برای اجرای الگوریتم k-means بسازید. به این منظور باید از آرگومانهای پیشفرض زیر در کلاسKMeans استفاده کنید:
- Init : به جای
randomباید ازk-means++استفاده کنید، تا مطمئن شوید نقاط مرکزی بهنحوی مقداردهی میشوند که بین آنها فاصله وجود داشته باشد. - n_init : باید تعداد مقداردهیهای اولیه را افزایش دهید، تا مطمئن شوید راهحل پایداری پیدا خواهید کرد.
- max_iter : همچنین تعداد تکرارها را بهازای مقداردهیهای اولیه افزایش میدهیم، تا مطمئن شویم k-means به همگرایی میرسد.
در کد زیر روال پردازشی الگوریتم خوشهبندی k-means را مشاهده میکنید که آرگومانهای آن از سوی کاربر در سازنده Constructor
KMeans تعریف شدهاند:
clusterer = Pipeline(
[
(
"kmeans",
KMeans(
n_clusters=n_clusters,
init="k-means++",
n_init=50,
max_iter=500,
random_state=42,
),
),
]
)
برای ایجاد یک روال پردازشی بزرگتر میتوان کلاس Pipeline را بهصورت زنجیری استفاده کرد. با تعریف clusterer و preprocessor در داخل Pipeline میتوان یک روال پردازشی کامل برای k-means ساخت.
pipe = Pipeline(
[
("preprocessor", preprocessor),
("clusterer", clusterer)
]
)
با فراخوانی .fit() و دادن متغیر data بهعنوان آرگومان به آن، تمامی مراحل تعریفشده در روال پردازشی، روی دادهها اجرا میشوند:
In [14]: pipe.fit(data)
Out[14]:
Pipeline(steps=[('preprocessor',
Pipeline(steps=[('scaler', MinMaxScaler()),
('pca',
PCA(n_components=2, random_state=42))])),
('clusterer',
Pipeline(steps=[('kmeans',
KMeans(max_iter=500, n_clusters=5, n_init=50,
random_state=42))]))])
به این ترتیب، روال پردازشی بهطور خودکار تمامی مراحل لازم برای اجرای الگوریتم k-means روی دادههای بیان ژن را اجرا میکند. شیءهای تعریفشده در روال پردازشی با فراخوانی نام مرحله خود قابل دسترس هستند.
حال باید با محاسبه ضریب silhouette عملکرد مدل را بسنجیم:
In [15]: preprocessed_data = pipe["preprocessor"].transform(data)
In [16]: predicted_labels = pipe["clusterer"]["kmeans"].labels_
In [17]: silhouette_score(preprocessed_data, predicted_labels)
Out[17]: 0.5118775528450304
برچسبهای واقعی را داریم، پس میتوانیم ARI را نیز محاسبه کنیم:
In [18]: adjusted_rand_score(true_labels, predicted_labels)
Out[18]: 0.722276752060253
همانطور که قبلتر نیز اشاره شد، مقدار عددی هر دو معیار ارزیابی عملکرد خوشهبندی عددی بین 1- و 1 است. وقتی مقدار ضریب silhouette صفر باشد، به این معناست که خوشهها بهشدت با یکدیگر همپوشانی دارند، اما وقتی مقدار این ضریب 1 به دست آید، به این معناست که خوشهها کاملاً از هم تفکیک شدهاند. همچنین، وقتی مقدار ARI صفر باشد، حاکی از این است که برچسب خوشهها کاملاً تصادفی تخصیص داده شدهاند و وقتی مقدار آن برابر 1 به دست آید، حاکی از این است که برچسبهای واقعی و پیشبینیشده یکسانند.
در مرحله PCA از روال پردازشی k-means، پارامتر n_components را برابر 2 قرار دادیم، به همین دلیل نیز الان میتوانیم هم برچسبهای واقعی و هم پیشبینیشده را به تصویر بکشیم. بهمنظور رسم نمودار از دیتافریم pandas و کتابخانه seaborn استفاده میکنیم:
pcadf = pd.DataFrame(
pipe["preprocessor"].transform(data),
columns=["component_1", "component_2"],
)
pcadf["predicted_cluster"] = pipe["clusterer"]["kmeans"].labels_
pcadf["true_label"] = label_encoder.inverse_transform(true_labels)
plt.style.use("fivethirtyeight")
plt.figure(figsize=(8, 8))
scat = sns.scatterplot(
"component_1",
"component_2",
s=50,
data=pcadf,
hue="predicted_cluster",
style="true_label",
palette="Set2",
)
scat.set_title(
"Clustering results from TCGA Pan-Cancer\nGene Expression Data"
)
plt.legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0.0)
plt.show()
نمودار حاصل از این کد به شکل زیر خواهد بود
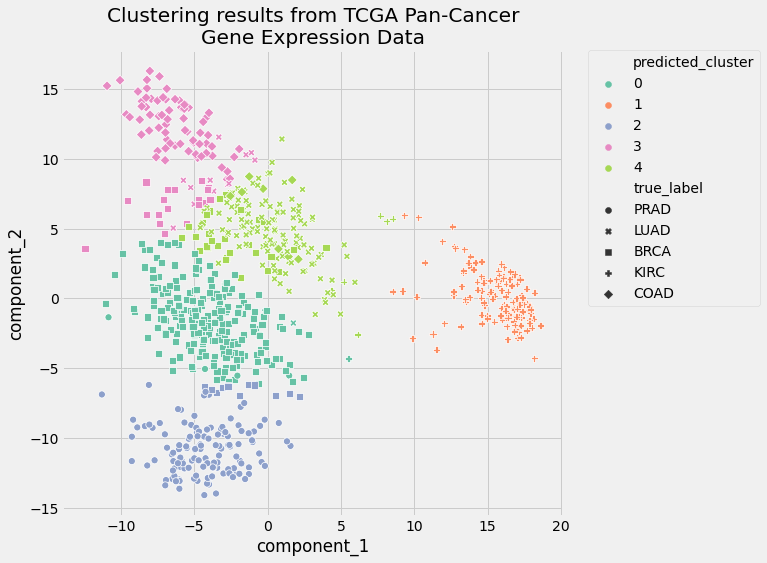
این نمودار، مهر تأییدی است بر نتایج معیارهای ارزیابی. خوشهها همپوشانی ناچیزی با یکدیگر دارند و تخصیص خوشهها بسیار بهتر از آن است که بتوان گفت تصادفی انجام گرفتهاند. بنابراین باید گفت که عملکرد روال پردازشی طراحیشده بسیار خوب بوده است.
تنظیم مجدد روال پردازشی الگوریتم خوشهبندی K میانگین
روال پردازشی الگوریتم k-means در این مقاله، عملکرد خوبی داشت، اما هنوز هم جا برای بهتر شدن دارد. دلیل اصلی ساخت روال پردازشی نیز این است که میتوان بعدها با تنظیم مجدد پارامترهای آن، نتایج خوشهبندی را به نتایج مطلوب نزدیکتر کرد.
فرایند تنظیم پارامترها Parameter tuning به این ترتیب است که هر بار مقدار ورودی یکی از پارامترها را تغییر میدهیم و نتایج جدید الگوریتم را ثبت میکنیم. در پایان فرایند تنظیم پارامترها، برای هر مقدار جدیدی که برای پارامترهای مختلف تعریف شده، یک مقدار نیز برای معیارهای ارزیابی عملکرد خواهیم داشت. به همین دلیل نیز تنظیم پارامترها روشی قدرتمند برای حداکثرسازی عملکرد روال پردازشی خوشهبندی در نظر گرفته میشود.
با تعریف مقدار 2 برای پارامتر n_components در مرحله PCA، در واقع تمامی ویژگیها را در دو مؤلفه یا بعد خلاصه کردیم. این امر کار ما را در مرحله مصورسازی دادهها و رسم نمودار دو بعدی آسان کرد؛ اما استفاده از تنها دو مؤلفه به این معناست که در مرحله PCA واریانس تشریحشده Explained variance
همه دادههای ورودی در نظر گرفته نمیشود.
واریانس تشریحشده اختلاف بین دادههای ورودی اصلی و دادههایی را که با روش PCA تبدیل شدهاند، اندازهگیری و بیان میکند. رابطه بین پارامتر n_components و واریانس تشریحشده را میتوان روی نمودار رسم کرد و مشاهده کرد که بهمنظور در نظر گرفتن درصد معینی از واریانس دادههای ورودی، PCA باید چه تعداد مؤلفه داشته باشد. علاوه بر این، میتوانید به کمک معیارهای ارزیابی عملکرد الگوریتم خوشهبندی نیز تعداد مؤلفهها لازم برای رسیدن به نتیجه مطلوب را به دست آورید.
در این مثال میخواهیم با استفاده از معیارهای ارزیابی عملکرد، تعداد مؤلفههای PCA را به دست آوریم. کلاس Pipeline در این شرایط کمک زیادی به ما میکند، چون میتوانیم با یک حلقه for عملیات تنظیم پارامترها را در آن انجام دهیم.
به این منظور کافی است حلقهای تعریف کنیم که مقدار n_components را در یک رنج خاص تعریف کرده و کد را به ازای هر مقدار تکرار میکند و سپس مقدار معیارهای ارزیابی را برای هر تکرار ثبت کنیم:
# Empty lists to hold evaluation metrics
silhouette_scores = []
ari_scores = []
for n in range(2, 11):
# This set the number of components for pca,
# but leaves other steps unchanged
pipe["preprocessor"]["pca"].n_components = n
pipe.fit(data)
silhouette_coef = silhouette_score(
pipe["preprocessor"].transform(data),
pipe["clusterer"]["kmeans"].labels_,
)
ari = adjusted_rand_score(
true_labels,
pipe["clusterer"]["kmeans"].labels_,
)
# Add metrics to their lists
silhouette_scores.append(silhouette_coef)
ari_scores.append(ari)
بهمنظور مشاهده رابطه میان تعداد مؤلفهها و عملکرد الگوریتم k-means نیز میتوانیم نمودار معیارهای ارزیابی بهعنوان تابعی از n_components را رسم کنیم:
plt.style.use("fivethirtyeight")
plt.figure(figsize=(6, 6))
plt.plot(
range(2, 11),
silhouette_scores,
c="#008fd5",
label="Silhouette Coefficient",
)
plt.plot(range(2, 11), ari_scores, c="#fc4f30", label="ARI")
plt.xlabel("n_components")
plt.legend()
plt.title("Clustering Performance as a Function of n_components")
plt.tight_layout()
plt.show()
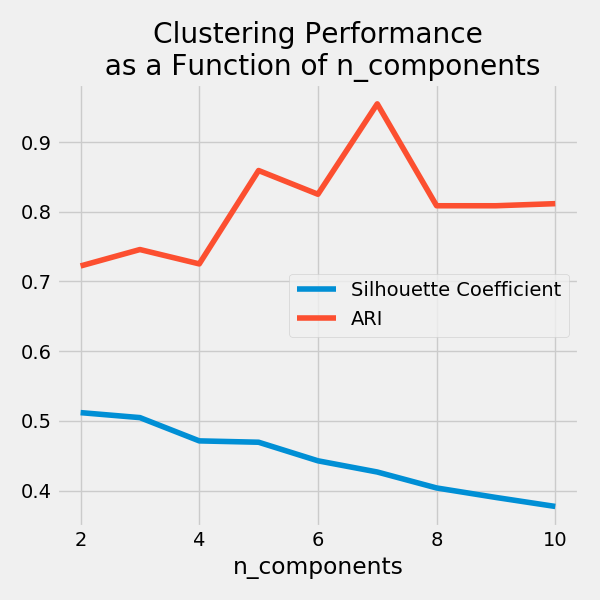
از این نمودار دو نتیجه میتوان گرفت:
- ضریب silhouette بهصورت خطی کاهش پیدا میکند. مقدار این ضریب در حقیقت به فاصله میان نقاط بستگی دارد، بنابراین با افزایش ابعاد، پراکندگی نیز افزایش مییابد.
- همانطور که مشاهده میکنید، ARI ابتدا با افزایش تعداد مؤلفه افزایش مییابد، اما بعد از رسیدن
n_componentsبه 7 مقدارARI شروع به کاهش میکند. بنابراین، وقتی تعداد مؤلفهها 7 تا باشد، این ورال پردازشی بهترین نتایج و بهترین خوشهها را ارائه خواهد داد.
در این مسئله نیز مشابه سایر مسائل یادگیری ماشینی، در هنگام بهینهسازی معیارهای ارزیابی باید هدف از خوشهبندی را نیز مدنظر قرار دهید. در مواقعی که برچسبهای واقعی خوشهها در دسترس هستند (مثل این مسئله)، معیار ARI انتخاب بهتری برای ارزیابی عملکرد است، چراکه این معیار برآورد میکند که دقت روال پردازشی شما در تخصیص مجدد برچسب خوشهها چقدر بوده است.
اما ضریب silhouette زمانی کاربرد دارد که خوشهبندی، کاوشگرانه Exploratory باشد، زیرا این معیار به شناسایی زیرخوشهها کمک میکند. این زیرخوشهها به ما میگویند که بررسیهای بیشتر لازم است و این امر میتواند منجر به کشف اطلاعات جدید و مهمی در دادهها شود.
نتیجهگیری
حال شما میدانید که چطور باید الگوریتم k-means را در پایتون اجرا کنید. روال پردازشی که در این مقاله آموزشی طراحی کردید، قادر است بیماران را بر اساس نوع سرطانشان خوشهبندی کند. میتوانید تکنیکهایی که در این مقاله آموختید را روی سایر دیتاستها نیز پیاده کنید، نتایج خوشهبندی خود را بهبود ببخشید و اطلاعات بهدستآمده را با سایرین به اشتراک بگذارید.
در این مقاله آموختید:
- تکنیکهای پرکاربرد خوشهبندی چه هستند و چه زمانی میتوان از آنها استفاده کرد،
- الگوریتم k-means چیست،
- چگونه میتوان k-means را در پایتون اجرا کرد،
- چگونه میتوان عملکرد الگوریتمهای خوشهبندی را ارزیابی کرد،
- چگونه میتوان یک روال پردازشی قدرتمند برای k-means ساخت و پارامترهای آن را تنظیم کرد،
- و چگونه میتوان نتایج حاصل از الگوریتم k-means را تحلیل کرده و توضیح داد.
همچنین در این مقاله نگاهی داشتیم به کتابخانه scikit-learn و ابزارهای قدرتمندی که برای پیادهسازی الگوریتم k-means در پایتون در اختیار ما قرار میدهد. اگر میخواهید خودتان مثالهای ذکرشده در این مقاله را اجرا کنید، با کلیک بر روی این لینک، میتوانید کدهای مربوطه بارگیری نمایید.





