با یادگیری بدون نظارت برای سفر به پاریس برنامهریزی کنید
تاکنون به این موضوع فکر کردهاید که یادگیری بدون نظارت برای سفر میتواند به شما در برنامهریزی سفر به پاریس کمک کند؟ با ما همراه باشید تا بگوییم چگونه این کار شدنی است. ابتدا ما فهرستی از چشماندازها و مکانهای دیدنی پاریس تهیه کردهایم تا علاقمندان از آن استفاده کنند. پس از اینکه فهرستبندی مکانها و جاذبههای گردشگری به پایان رسید، یک نقشه گوگل هم ساخته شد.
مشاهده تمامی جاذبههای گردشگری پاریس به برنامهریزی خاصی احتیاج دارد؛ اما سوال اینجاست که چطور میتوان تصمیم گرفت از کدام جاذبهها در وهله اول دیدن کرد و از چه ترتیبی باید پیروی کرد؟ ما این کار را به منزلۀ یک مسئله خوشهبندی تلقی میکنیم. روش یادگیری بدون نظارت برای سفر میتواند نقش مهمی در حل این مسئله ایفا کند.
الگوریتم هایی نظیر K-Means یا DBScan هم در این مسئله میتوانند به کار آیند. اما در ابتدا باید دادهها را آماده کرد تا چنین الگوریتمهایی مطابق خواستهها عمل کند.
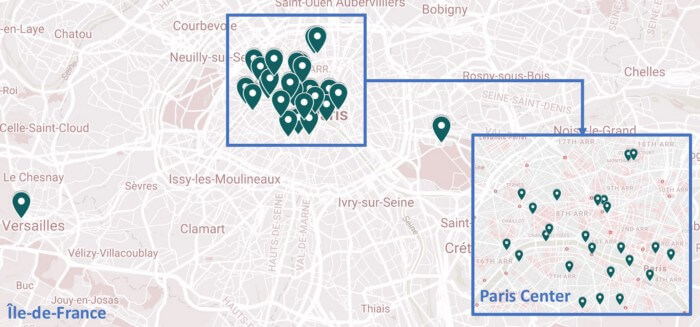
یادگیری بدون نظارت برای سفر موقعیتهای جغرافیایی
پیش از هرچیز برای یادگیری بدون نظارت برای سفر موقعیتهای جغرافیایی را در پین نقشه گوگل با فرمت دوبعدی بررسی کردیم. تبدیل پینها به طول جغرافیایی Longitude و عرض جغرافیایی Latitude میتواند اقدام بسیار خوبی باشد. ما به دنبال راهی سریعتر برای استخراج این اطلاعات از نقشه گوگل بودیم. StackOverflow کمک میکند تا به همه خواستههایمان برسیم. شما باید به این لینک مراجعه کرده و فایل *.kmz را دانلود کنید. سپس باید این فایل را به فایل *.zip تغییر دهید. در وهله بعد، نوبت به استخراج فایل و باز کردن doc.kml با نرمافزار ویرایش متن دلخواهتان میرسد (ما از SublimeText استفاده میکنیم).
حال، میتوانید از فرمان CTRL+F برای جستجوی فیلدها استفاده کنید یا از BeautifulSoup استفاده کنید (همان طور که در ذیل مشاهده میکنید). به محض استخراج مختصات از فایل XML، مختصات را در دیتافریم ذخیره کردم. در مجموع 26 مکان دیدنی وجود دارد (که با عنوان در فایل XML ذخیره شده است).
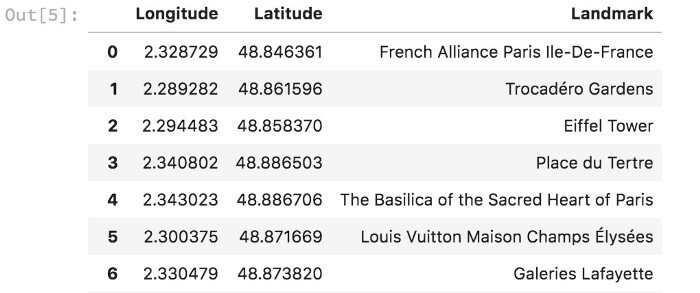
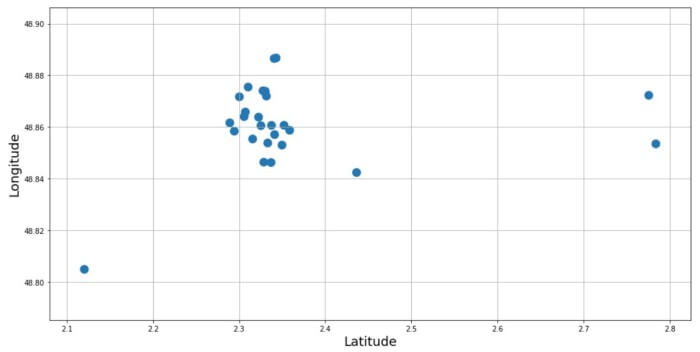
ما از دیتافریمی که مختصات و نام مکانهای دیدنی در آن ذخیره شده بود، برای ایجاد نقشه پراکندگی استفاده کردیم.
خوشهبندی K-Means
زمانی که ابهام در پیامد مورد پیشبینیمان وجود داشته باشد، روشهای یادگیری بدون نظارت عموماً برای دادههایی که فاقد برچسبهای AND هستند، بسیار مفید واقع میشوند. این الگوریتمها معمولاً به دو شکل قابل دسترس هستند:
1) الگوریتمهای خوشهبندی
2) الگوریتمهای کاهش بُعد
در این بخش، میخواهیم عمده تمرکزمان را روی الگوریتم خوشهبندی K-Means بگذاریم. در این الگوریتم، تعداد خوشهها به عنوان ورودی از پیش تعیین شده است و الگوریتم به ایجاد خوشهها در دیتاست بدون برچسب میپردازد. K-Means مجموعهای از نقاط مرکزی خوشه K و برچسبی از چیدمان ورودی X ایجاد میکند. به این ترتیب، کلیه نقاط واقع در X به خوشه منحصربفردی اختصاص داده میشوند. این الگوریتم نقاط مرکزی خوشهها را به عنوان میانگین کلیه نقاط متعلق به خوشه محاسبه میکند.

این کار با پایتون به شکل زیر انجام میشود:
همانطور که از نمودار پراکندگی زیر پیداست، ما 10 خوشه ساختم؛ یعنی یک خوشه برای هر روز از سفر. چون مراکز دیدنی در مرکز پاریس فاصله نزدیکی با هم دارند، تفکیک یک خوشه از خوشه دیگر کار دشواری است.
پیشبینیها مرتب شده و در دیتافریم ذخیره شدند. k-means برای ایجاد 10 خوشه مورد استفاده قرار گرفت. نقاط سیاه مرکز خوشهها را نشان میدهند. من از 10 خوشهای که با k-means ایجاد شده بود، برای ساخت دیتافریمی استفاده کردم که روزهای هفته را به هر خوشه تخصیص میدهد. به این ترتیب، یک نمونه برنامه زمانی به دست میآید.
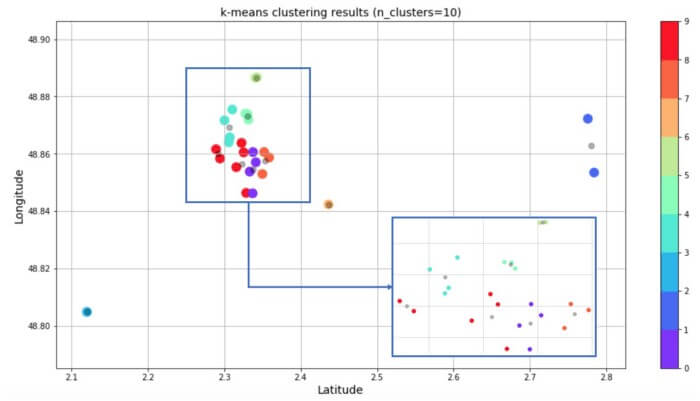
اکنون، در این مرحله، دیتافریم مرتب شده و پینهای نقشه گوگل مجدداً ساماندهی میشوند (هر لایه نشاندهندۀ یک روز است). خودشه! برنامه سفر تهیه شد.

اما یک مورد همچنان اذیتکننده است. k-means بر اساس فاصله اقلیدسی میان نقاط به خوشهسازی میپرداخت. اما میدانیم که زمین تخت نیست؛ مابه دنبال بررسی این مسئله بودیم که آیا این تقریب بر خوشههای ایجاد شده تاثیر میگذارد یا خیر. باید به این نکته هم توجه داشت که چند نقطه دیدنی با فاصله از مرکز پاریس واقع شده است.

با HDBSCAN آشنا شوید!
پس به یک روش خوشهبندی احتیاج داریم که فواصل جغرافیایی (طول کوتاهترین منحنی میان دو نقطه در امتداد سطح زمین) را بطور کارآمد مدیریت کند.

تابع تراکم جمعیت HDBSCAN که بر پایه الگوریتم DBScan Density-based spatial clustering of applications with noise قرار دارد، میتواند نقش سودمندی در این فرایند داشته باشد. هر دو الگوریتمِ HDBSCAN و DBSCAN از جمله روشهای خوشهبندی مکانی به شمار میروند و بر پایه تراکم قرار دارند.
این الگوریتمها بر اساس اندازهگیری فاصله و تعداد حداقلی نقاط، به گروهبندی آن دسته از نقاطی میپردازند که در فاصله نزدیکی به همدیگر واقع شدهاند. این الگوریتمها داده پرتها را نیز در مناطقی با تراکم پایین تعیین میکنند. خوشبختانه، HDBSCAN از طول جغرافیایی و عرض جغرافیایی هم پشتیبانی میکند. بنابراین، زمینه برای محاسبه میان موقعیتهای جغرافیایی فراهم میآید.
HDBSCAN در نسخه عادی پایتون منظور نشده است، پس مجبورید آن را به صورت pip یا conda نصب کنید. پس از این کار کد زیر را به جرا درآوردیم. سرانجام، دیتافریم و نمودار پراکندگی زیر به دست آمد. همان طور که ملاحظه میکنید، نقاط مجزا در خوشه 1- جای دارند؛ پس این نقاط «نویز» به حساب میآیند.
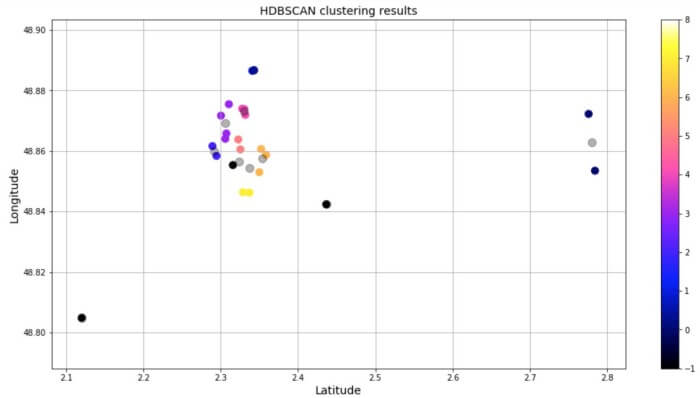
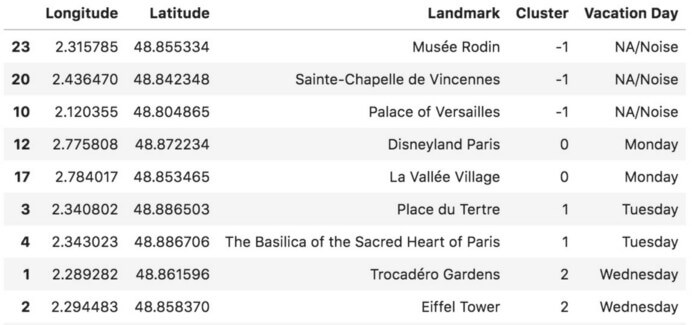
اصلاً تعجببرانگیز نیست که چندین نقطه به عنوان نویز وجود داشته باشد. چون حداقل تعداد نقاط در خوشه HDBSCAN برابر است با 2، نقاط مجزا از قبیل کاخ ورسای به عنوان نویز طبقهبندی شدهاند. مکانهایی نظیر کلیسای Sainte-Chapelle de Vincennes و موزه Musée Rodin با سرنوشت مشابهی روبرو شدند.
اما نکته جالب به تعداد خوشههایی مربوط میشود که HDBSCAN شناسایی کرد (یعنی 9 عدد). روش خوشهبندیِ مورد استفاده در این پست آموزشی میتواند ارتقاء یابد. برای نمونه، میتوان ویژگی وزن را در نقاط داده به کار برد. وزنها میتوانند مقدار زمان مورد نیاز برای بازدید از یک مکان دیدنی را نشان دهند. به این ترتیب، تعداد کل نقاط داده در خوشه تحت تاثیر قرار میگیرد.