
توابع فعال سازی: سیگموید، ReLU ،Leaky ReLU و Softmax در شبکههای عصبی
در این نوشتار به بررسی و مطالعه مبانی نورونها، شبکه های عصبی و توابع فعال سازی میپردازیم. شبکههای عصبی مصنوعی از نورونها تشکیل میشوند. هر نورون را میتوان یک تابع در نظر گرفت که عددی در خود جای داده است. نورونها این جریان/ورودی را از انشعابات انتهایی (سیناپسها) دریافت میکنند. در هر یک از لایههای شبکه عصبی، ورودی نورون را در وزن سیناپس ضرب میکنیم و مجموع آن را به دست میآوریم.
نمونه کد برای انجام عملیات پیشانتشار در نورون
class Neuron(object):
# ...
def forward(self, inputs):
""" assume inputs and weights are 1-D numpy arrays and bias is a number """
cell_body_sum = np.sum(inputs * self.weights) + self.bias
firing_rate = 1.0 / (1.0 + math.exp(-cell_body_sum)) # sigmoid activation function
return firing_rate

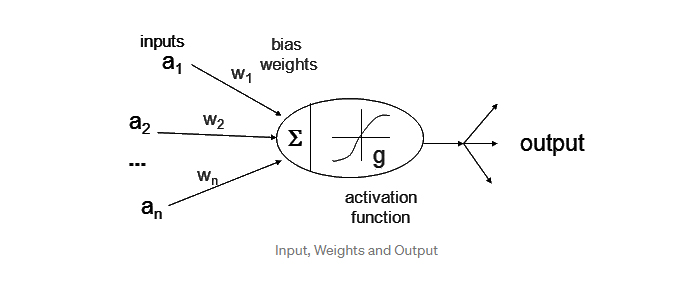
برای مثال، (به D در شکل فوق نگاه کنید) با فرض اینکه وزنها برابر با w1, w2, w3, … wN و ورودیها برابر با i1, i2, i3, … iN باشند، مجموع آنها برابر با w1*i1 + w2*i2 + w3*i3 … wN*iN خواهد بود.
در شبکههای عصبی، مقادیر wX و iX از لایهای به لایه دیگر و از اتصالی به اتصال دیگر متفاوت است و مجموع s بسته به فعال بودن و غیرفعال بودن نورون متغیر است. در شبکههای عصبی برای نرمالسازی مقادیر از توابع فعال سازی استفاده میکنیم؛ این تابع مقادیر را به گونهای تبدیل میکند تا در مقیاس 0 و 1 و یا 1- و 1 قرار گیرند.
از جمله ویژگیهای توابع فعال سازی میتوان به موارد زیر اشاره کرد:
- غیرخطی بودن: غیرخطی بودن تابع فعالسازی به این معنی است که یک شبکه عصبی دو لایه را میتوان نوعی تابع عمومی تقریب Universal function approximator در نظر گرفت. تابع فعالسازی identity خطی است. به عبارت دیگر، اگر چندین لایه به صورت همزمان از این تابع فعالسازی استفاده کنند، شبکه عصبی به مثابه یک مدل یک لایه عمل خواهد کرد.
- بازه: در صورتیکه بازهی (Range) تابع فعالسازی محدود باشد، متدهای آموزشی مبتنی بر گردایان پایدارتر خواهند بود، چراکه الگوها فقط تعداد کمی از وزنها را تحت تأثیر میگذارند. از سوی دیگر، اگر بازهی تابع فعالسازی غیرمحدود و نامتناهی باشد، فرایند آموزش کاراتر و اثربخشتر خواهد بود، زیرا الگوها بر بیشتر وزنها اثر میگذارند. در مورد آخر، به نرخهای یادگیری کوچکتر نیاز است.
- مشتقپذیر پیوسته: در توابع فعال سازی، این ویژگی از آن جهت مطلوب است که در متدهای بهینهسازی مبتنی بر گرادیان کاربرد دارد (تابع ReLU مشتقپذیر پیوسته نیست و به همین دلیل در بهینهسازی مبتنی بر گرادیان به مشکل میخورد). تابع پلهای دودیی Binary step function در 0 مشتقپذیر نیست و برای تمامی مقادیر در 0 مشتق میشود، به همین دلیل آن دسته از متدهای مبتنی بر گرادیان که از این تابع استفاده میکنند، پیشرفتی نخواهند داشت.
|
- یکنوا Monotonic: در صورتیکه تابع فعالسازی یکنوا باشد، متغیر خطای مدل یک لایه محدب خواهد بود.
|
- توابع هموار با مشتق یکنوا: این نوع توابع در برخی موارد عملکرد بهتری در امر تعمیمدهی دارند.
- موجودیت را نزدیک به ریشه یک تابع (صفرها) تقریب میزند: چنانچه تابع این ویژگی را داشته باشد و وزنهای شبکه عصبی با مقادیر تصادفی مقداردهی شوند، یادگیری شبکه کارا خواهد بود. اگر تابع فعالسازی موجودیت را نزدیک به ریشه تقریب نزند، باید در مقداردهی وزنهای توجه بیشتری به خرج دهیم.
جدول توابع فعال سازی

مقدمهای بر توابع فعال سازی
1-تابع سیگموید
در یادگیری ماشین، برای پیادهسازی شبکههای عصبی ساده و رگرسیون لجستیک از توابع سیگموید استفاده میشود. این توابع، واحدهای فعالسازی مقدماتی هستند. اما با توجه به ایرادت و نواقص توابع سیگموید ترجیح بر این است که از این توابع در شبکههای عصبی پیشرفته استفاده نشود.

تابع سیگموید و مشتق آن ساده هستند و مدت زمان ساخت مدل را کاهش میدهند، اما از آنجایی که بازه مشتق آن کوتاه است، در این تابع با مشکل info loss مواجه هستیم:

لذا، هرچه شبکه عصبی ما لایههای بیشتری داشته باشد و یا به عبارتی عمیقتر باشد، در هر لایه اطلاعات بیشتری فشردهسازی میشوند و حذف میشوند. در نتیجه دادههای بیشتری از بین میروند.
| تابع سیگموید علاوه بر تابع لجستیک، تابع معکوس مثلثاتی Arctangent، تانژانت هذلولوی Hyperbolic tangent، تابع Gudermannian، تابع خطا، تابع لجستیک تعمیمیافته و توابع جبری را در بر میگیرد. (برگرفته از ویکیپدیا) |
2- تابع ReLU
| ReLU، از سال 2018 تا به امروز، به عنوان محبوبترین تابع فعالسازی در شبکه های عصبی عمیق شناخته میشود. |
در حال حاضر، بیشتر برنامههای یادگیری عمیق برای انجام مسائل مرتبط با بینایی کامپیوتر، پردازش متن، تشخیص صوت و شبکههای عصبی عمیق به جای توابع فعال سازی لجستیک از تابع ReLU استفاده میکنند.
تابع ReLU انواع گوناگونی دارد: Softplus (SmoothReLU)، Noisy ReLU، Leaky ReLU، Parametric ReLU و ExponentialReLU (ELU).
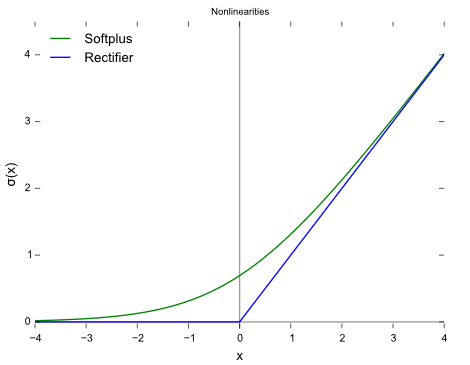
تابع فعالسازی ReLU: در صورتیکه ورودی کمتر از 0 باشد، تابع فعالسازی ReLU صفر (0) و در غیر اینصورت مقدار خام را خروجی میدهد. به عبارت دیگر، اگر مقدار ورودی بیشتر از 0 باشد، تابع ReLU همان مقدار ورودی را خروجی میدهد. عملکرد تابع فعالسازی ReLU از جهات بسیاری مشابه عملکرد نورونهای زیستی ما است:

ReLU یک تابع غیرخطی است و برخلاف تابع سیگموید با خطاهای پسانتشار مواجه نمیشود. علاوه بر این، اگر در شبکههای عصبی بزرگتر به جای تابع سیگموید از تابع ReLU استفاده کنیم، سرعت مدلسازی بیشتر خواهد بود، به عبارت دیگر مدت زمان مدلسازی کاهش مییابد:
- باورپذیری بیولوژیکی: این تابع برخلاف تابع پادتقارن Antisymmetry tanh ، یک جانبه است.
- فعالسازی پراکنده Sparse activation: برای مثال، در شبکهای که به صورت تصادفی مقداردهی شده است، حدود 50 درصد از واحدهای پنهان، فعال میشوند ( و خروجی آنها غیرصفر خواهد بود).
- انتشار بهتر گرادیان: در این تابع برخلاف توابع فعال سازی سیگموید کمتر با مشکل محوشدگی گرادیان gradient vanishing مواجه میشویم.
- محاسبات اساسی: در این تابع فقط از مقایسه، جمع و ضرب استفاده میشود.
- مقیاسپذیر: max ( 0, a x ) = a max ( 0 , x ) for a ≥ 0
توابع ReLU هم کاستیهایی دارند. برای مثال، میانگین این تابع صفر نیست و در صفر مشتق نمیشود، اما در هر جای دیگری مشتق میشود.

مشکل دیگری که در تابع ReLU با آن مواجه هستیم، مشکل مرگ ReLU است. منظور از مرگ ReLU این است که برخی از نورونهای ReLU میمیرند و غیرفعال میشوند و برای تمامی ورودیها، صفر (0) را خروجی میدهند. در این حالت، هیچ گرادیانی جریان نمیابد و در صورتیکه تعداد نورونهای غیرفعال در شبکه عصبی زیاد باشد، عملکرد مدل تحت تأثیر قرار میگیرد. برای حل این مشکل میتوانیم از تابع Leaky ReLU استفاده کنیم؛ Leaky ReLU در نمودار بالا همان قسمتی است که شیب در سمت چپ x=0 تغییر کرده است و در نتیجه باعث گسترش یا به اصطلاح نشتی بازه تابع ReLU میشود.

3- تابع فعالسازی Softmax
تابع فعالسازی softmax بسیار جالب است، به این دلیل که این تابع علاوه بر نگاشت مقیاس/ بازه خروجی به [0، 1]، هر خروجی را به نحوی نگاشت میکند که مجموع آن برابر با 1 باشد. خروجی تابع فعالسازی softmax یک توزیع احتمالی است.
| از تابع softmax اغلب در لایه آخر کلاسیفایر شبکه عصبی استفاده میشود. اینگونه شبکهها معمولاً بر روی log loss آموزش میبینند. در این شبکهها از یکی از انواع غیرخطی رگرسیون لجستیک چندجملهی، استفاده میشود. برگرفته از ویکیپدیا |

معادله ریاضی تابع Softmax به شکل زیر است؛ در این معادله z بُردار ورودیها به لایه خروجی است و j واحدهای خروجی را 1, 2, 3 … k تعدیل میکند:

در مدل رگرسیون لجستیک از تابع softmax برای طبقهبندی چندگانه و از تابع سیگموید برای طبقهبندی دودویی استفاده میشود. مجموع احتمالات برای تابع softmax صفر (0) است.
برای درک بهتر این توابع به شما توصیه میکنم نمودار و مشتقاتشان را در پایتون/ متلب و R ترسیم کنید و به مقادیر مینیمم، ماکسیمم و بازههای آنها نیز توجه کنید و تغییراتی که در نتیجه ضرب اعداد در این مقادیر حاصل میشود را بررسی کنید.






