توضیح ساده و جامع مدل پنهان مارکوف (HMM)

مدل پنهان مارکوف (HMM) یک ابزار مدل‌سازی آماری بسیار قدرتمند به شمار می‌رود که در حوزه‌هایی همچون تشخیص گفتار Speech recognition، تشخیص دست‌خط Handwriting recognition و غیره کاربرد دارد. زمانی که خواستیم از این مدل استفاده کنیم متوجه شدیم توضیحات جامع و واضحی در مورد آن وجود ندارد و مطالب موجود به اندازه‌ی کافی ساده و قابل‌فهم نیستند. مقالات علمی منتشرشده حول موضوع HMM نیز نوشتار دشوار و پیچیده‌ای دارند. به همین دلیل تصمیم گرفتیم در این مقاله توضیحی ساده از HMM برای علاقه‌مندان به این موضوع ارائه دهیم.

سؤالات مدل پنهان مارکوف (HMM)

مدل پنهان مارکوف (HMM) به این سؤالات پاسخ می‌دهد:

ارزیابی: احتمال وقوع یک حالت چقدر است؟ یا به بیان دیگر، احتمال یک دنباله از مشاهدات چقدر است؟

• الگوریتم پیش­رو Forward algorithm
• الگوریتم پس­رو Backward algorithm
• …

رمزگشایی: دلیل مشاهده‌ای که اتفاق افتاده چیست؟ یا به بیان دیگر، وقتی یک دنباله از مشاهدات دارید، محتمل‌ترین دنباله‌ی حالت‌های پنهان چیست؟

• الگوریتم Viterbi
• …

یادگیری: از مشاهدات موجود چه می‌توانیم بیاموزیم؟ به بیان دیگر، چطور می‌توان از مشاهدات یک یا چند مدل HMM ساخت؟

• Baum-Welch
• …

در مقالات بعدی به این سؤالات پاسخ خواهیم داد. در این نوشتار قصد داریم به جزئیات مدل HMM بپردازیم.

مدل پنهان مارکوف (HMM)

بخش‌های اساسی مدل HMM عبارت‌اند از:

• حالت‌های پنهان Hidden states
• نمادها (یا حالت‌ها)ی مشاهده
• توزیع احتمال انتفال transition از حالت ابتدایی به حالت پنهان ابتدایی
• توزیع احتمال انتفال به حالت نهایی (این مورد در مدل در نظر گرفته نمی‌شود، زیرا در حالت عمومی همه‌ی احتمالات برابر با 1 هستند).
• توزیع احتمال انتقال حالت
• توزیع احتمال تولید حالت State transition

در قسمت بعد این بخش‌های HMM را به صورت مفصل توضیح خواهیم داد.

حالت‌های پنهان و سمبل­های مشاهده‌شده

مدل پنهان مارکوف HMM دو بخش دارد: پنهان و مشاهده‌شده. بخش پنهان از حالات پنهانی تشکیل شده که مستقیماً قابل مشاهده نیستند، بلکه حضورشان توسط سمبل­های قابل مشاهده‌ای نمایان می‌شود که توسط حالت‌های پنهان تولید می‌شوند.

مثال 1: از خُلق الآن همسرتان آگاهی ندارید (خُلق یک حالت پنهان است)، اما رفتارهای او (نمادهای قابل مشاهده) را مشاهده می‌کنید و از این رفتارهای قابل مشاهده می‌توانید حالت پنهان (خلق) را حدس بزنید.

مثال 2: می‌خواهید از برنامه‌ی دوستتان باخبر شوید، اما فقط می‌توانید آب و هوا را مشاهده کنید. فعالیت‌های دوست شما (که حالت پنهان است) نمادهای قابل مشاهده‌ای تولید می‌کند (که شرایط آب و هواست)؛ شاید فکر کنید این رابطه معکوس است، یعنی وضعیت آب و هوا حالت پنهان و فعالیت‌های دوست شما نماد قابل مشاهده است، اما نکته اینجاست که در این مثال، شما می‌توانید آب و هوا را مشاهده کنید و نه فعالیت دوستتان.

در مثال اول نمادهای مشاهده‌شده از حالت‌های نهان تولید شده‌اند، اما در مثال دوم نمادهای مشاهده‌شده حکم علت حالت نهان (فعالیت‌های دوستان شما) را دارند. بنابراین می‌توان گفت سمبل­های قابل مشاهده می‌توانند دلیل مستقیم و یا نتیجه و پیامد حالت‌های پنهان باشند. هردوی این روابط امکان‌پذیر هستند و این از نقاط قوت HMM به شمار می‌رود. در کل حالت‌های پنهان (همچون خُلق، فعالیت دوستتان و …) که قابل مشاهده نیستند و سمبل­های قابل‌مشاهده (اقدامات، آب‌وهوا، و …)‌ را انتخاب می‌کنید.

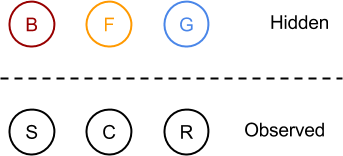
مصورسازی حالت‌های پنهان و مشاهده‌شده برای مثال 2

فعالیت دوست شما:

• بسکتبال (B)
• فوتبال (F)
• بازی ویدئویی (G)

نمادهای قابل مشاهده:

• آفتابی (S)
• ابری (C)
• بارانی (R)

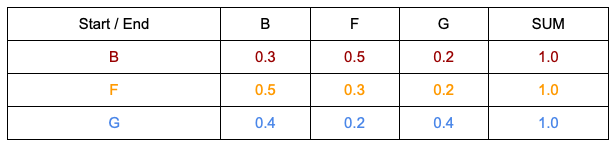
توزیع احتمال انتقال حالت

بعد از انتخاب حالت‌های پنهان مسئله، به توزیع احتمال انتقال حالت نیاز خواهید داشت که انتقال بین حالت‌های پنهان را توضیح می‌دهد. به صورت کلی می‌توان از هر حالتی به حالت دیگر انتقال پیدا کرد. بنابراین اگر 9 حالت داشته باشید، به یک ماتریس 9×9 نیاز دارید؛ پس برای N حالت، باید یک ماتریکس NxN داشته باشیم.

علاوه بر این، جمع احتمالات مربوط به همه‌ی گذارهایی که از حالت فعلی امکان‌پذیر هستند، 1 خواهد بود.

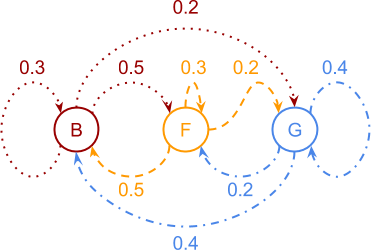
توزیع احتمالات تولید حالت

حالت‌های پنهان و نمادهای قابل مشاهده‌ی موجود به وسیله‌ی توزیع احتمالات تولید حالت به هم مربوط می‌شوند؛ بدین صورت که هر انتقال به حالت پنهان، یک نماد قابل مشاهده تولید می‌کند. علاوه بر این هر حالت پنهان می‌تواند همه‌ی نمادهای قابل‌مشاهده را تولید کند و تنها احتمال تولید اول یا نماد دیگر تفاوت دارد. جمع احتمالات تولید همه‌ی حالت‌های پنهان 1 خواهد بود.

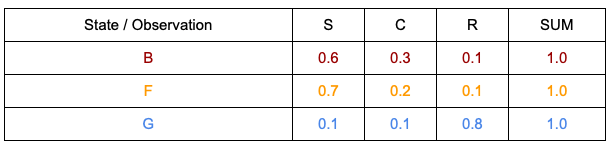
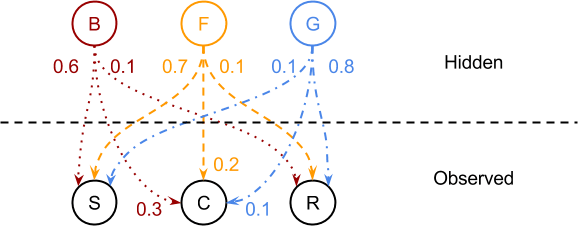
در تصویر بالا، توزیع احتمالات تولید حالت را مشاهده می‌کنید. این نمودار اطلاعات جدول قبلی را مستقیماً به نمایش گذاشته است.

توزیع احتمالات حالت ابتدایی/انتهایی

علاوه بر حالت پنهان، دو حالت دیگر هم وجود دارند که به صورت غیرمستقیم به مدل مرتبط می‌شوند و در محاسبات مورد استفاده قرار می‌گیرند:

• حالت ابتدایی
• حالت انتهایی

همانطور که گفتیم این دو حالت در محاسبات کاربرد دارند. زمانی‌که دنباله‌ای از سمبل­های مشاهده‌شده دارید که مربوط به حالت‌های پنهان هستند (انتقال به حالت‌های پنهان، نمادهای قابل مشاهده‌ تولید می‌کند)، دو مورد جانبی نیز خواهید داشت: زمانی که دنباله شروع می‌شود و زمانی‌که پایان می‌یابد.

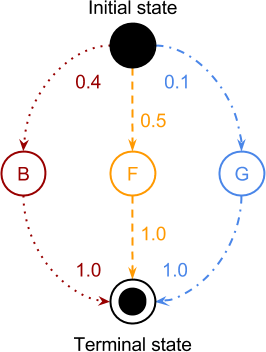
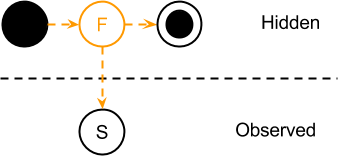
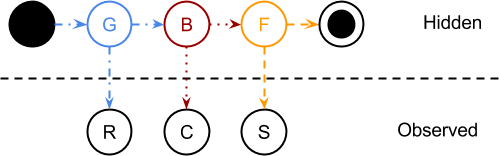
در زمان شروع دنباله یک سمبل برای نمونه S تولید می‌شود؛ اما تولید تنها زمانی رخ خواهد داد که انتقال به حالت‌های پنهان اتفاق بیافتد. اینجاست که حالت ابتدایی وارد کار می‌شود. به بیان دیگر، نماد S می‌تواند از انتقال به همه‌ی حالت‌های پنهان با احتمالات متفاوت تولید شود؛ اما تولید این نماد در انتقال به کدام حالت پنهان بیشترین احتمال را خواهد داشت؟ در نمودار قبلی می‌توانید میزان احتمال تولید S طی انتقال به حالت‌های پنهان را ببینید، اما این تصویر نشان نمی‌دهد گذار از کدام حالت انجام شده است، پاسخ به این سؤال ما را به حالت ابتدایی می‌رساند. در نتیجه می‌توان گفت وقتی یک دنباله‌ از مشاهدات آغاز می‌شود، حالت پنهان ابتدایی که نماد را تولید می‌کند توسط احتمال انتقال حالت ابتدایی مشخص می‌شود. شکل 5 همین موضوع را نشان می‌دهد (در شرایطی که یک دنباله‌ از مشاهدات فقط از یک نماد داشته باشیم).

تا این‌جا دریافتیم وقتی دنباله‌ای‌ از مشاهدات را آغاز می‌کنیم، باید حالت نهان اولیه را مشخص کنیم و توزیع احتمال حالت ابتدایی به این امر کمک خواهد کرد. زمانی که به انتهای دنباله می‌رسیم، در واقع یک انتقال به حالت انتهایی انجام شده است، زیرا هر دنباله‌ از مشاهدات به عنوان واحدهای مجزا پردازش می‌شود. این انتقال عموماً ضمنی بوده و آشکارا به آن اشاره‌ای نمی‌شود. علاوه بر این به صورت کلی، احتمال انتقال از هر حالت نهان به حالت انتهایی برابر با 1 است.

همانطور که در شکل بالا مشاهده می‌کنید، وقتی دنباله‌ی مشاهدات شروع می‌شود، حالت پنهان F محتمل‌ترین حالت پنهان است که نماد اولین دنباله‌ی مشاهدات را تولید می‌کند.

دنباله‌ی مشاهدات

دنباله‌ی مشاهدات دنباله‌ای از 1 تا N نماد قابل مشاهده است. هر دنباله‌ی مشاهدات به عنوان یک واحد مستقل و بدون استفاده از هرگونه دانشی نسبت به گذشته یا آینده مورد استفاده قرار می‌گیرد. به همین دلیل حالت پنهان به حالت‌های ابتدایی و انتهایی نیاز دارد.

نکته‌ی مهم این‌جاست که دنباله‌ی مشاهدات می‌تواند از یک دنباله‌ی حالت پنهان متفاوت (تصاویر 6 و 7) به دست بیاید. علاوه بر این، دنباله‌ی مشاهده‌ای باید حداقل یک نماد (شکل 5) داشته باشد و طول آن نیز می‌تواند هرمقداری باشد. تنها شرط این است که دنباله‌ی مشاهده‌ای پیوسته باشد، بدین معنی که دنباله هیچ جای خالی نداشته باشد.

جمع‌بندی

هدف از این مقاله آشنایی با مؤلفه‌های اساسی مدل پنهان مارکوف (HMM)، مقدمات، نحوه‌ی کار و بازنمایی آن و آموزش نحوه‌ی تولید دنباله‌ی مشاهدات از حالت‌های نهان بود.