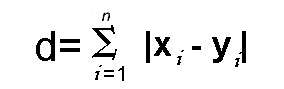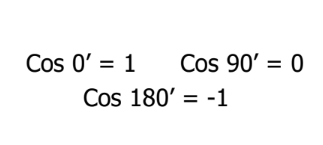اهمیت معیارهای فاصله در مدلسازی یادگیری ماشینی
برخی از الگوریتمهای یادگیری ماشینی (نظارتشده یا غیرنظارتشده) برای درک الگوی دادههای ورودی و تصمیمگیری بر اساس آنها، از معیارهای فاصله استفاده میکنند. یک معیار فاصله خوب میتواند به بهبود عملکرد ردهبندی، خوشهبندی و بازیابی اطلاعات کمک کند. در این نوشتار در مورد انواع معیارهای فاصله صحبت میکنیم و نقش آنها در مدلسازی یادگیری ماشینی را توضیح میدهیم.
مقدمه
از جمله کاربردهای الگوریتمهای یادگیری ماشینی در دنیای واقعی میتوان به ردهبندی یا تشخیص تصاویر و بازیابی اطلاعات موجود در آنها (برای مثال تشخیص چهره، تصاویر آنلاین سانسورشده، کاتالوگهای فروش، سیستمهای توصیهگر و…) اشاره کرد. انتخاب معیار فاصله از اهمیت بالایی برخوردار است؛ معیار فاصله به الگوریتمها کمک میکند، شباهت بین تصاویر گوناگون را تشخیص دهند.
ویکیپدیا یک تعریف ریاضیاتی ساده از معیار فاصله ارائه میدهد:
در معیار فاصله، از تابع فاصله استفاده میشود؛ تابع فاصله معیاری برای اندازهگیری فاصله بین اجزای دیتاست فراهم میآورد.
شاید بپرسید تابع فاصله چیست و چطور کار میکند؟ چطور میتواند تشخیص دهد یک جزء یا محتوای خاص با سایر اجزای دیتاست ارتباط دارد؟ در بخشهای بعدی به این سؤالات پاسخ میدهیم.
تابع فاصله
اگر قضیه فیثاغورس را به خاطر داشته باشید، احتمالاً میتوانید فاصله بین دو نقطهداده را با استفاده از این قضیه محاسبه کنید:
برای محاسبه فاصله بین دو نقطهداده A و B، قضیه فیثاغورس طول محور x و y را محاسبه میکند:
در الگوریتمهای یادگیری ماشین نیز برای محاسبه فاصله از این قضیه استفاده میشود. در الگوریتمها، فرمول بالا را بهعنوان تابع فاصله به کار میبریم. قسمتهای بعدی شامل توضیحات بیشتر در خصوص الگوریتمهایی است که از این فرمول استفاده میکنند.
پس تابع فاصله را میتوان بدین صورت تعریف کرد (منبع: Math.net):
تابع فاصله، فاصله بین اجزای یک مجموعه را محاسبه میکند. اگر فاصله صفر باشد، آن نقاط (اجزاء) برابر هستند و در غیر این صورت، با یکدیگر تفاوت دارند.
به بیان دیگر، تابع فاصله صرفاً یک فرمول ریاضیاتی است که در معیارهای فاصله به کار میرود. هرکدام از معیارهای فاصله از توابع فاصله گوناگون استفاده میکنند. در خصوص معیارهای فاصله و نقش آنها در مدلسازی یادگیری ماشینی صحبت خواهیم کرد.
معیارهای فاصله
چندین معیار فاصله وجود دارد، اما در این نوشتار تنها تعدادی از پرکاربردترین آنها را مورد بررسی قرار میدهیم. ابتدا سعی میکنیم منطق ریاضیاتی زیربنایی این معیارها را توضیح دهیم و سپس، الگوریتمهای یادگیری ماشینی را که از این معیارها استفاده میکنند، معرفی خواهیم کرد.
از جمله معیارهای پرکاربرد فاصله میتوان به این موارد اشاره کرد:
معیار مینکفسکی
معیار مینکفسکی معیاری در فضای برداری نرمالشده است. فضای برداری نرمالشده یک فضای برداری است که نُرم آن مشخص است. اگر X یک فضای برداری باشد، نُرم آن تابعی با مقادیر حقیقی ||x|| است که شرایط زیر را باید برآورده کند:
- 1. بردار صفر: طول بردار صفر، صفر خواهد بود.
- 2. عامل مقیاسبند: اگر بردار را در یک عدد مثبت ضرب کنیم، جهت آن تغییر نمیکند، اما طول آن تغییر خواهد کرد.
- 3. نابرابری مثلثی: اگر فاصله، نُرم باشد، فاصله محاسبهشده بین دو نقطه همواره یک خط صاف خواهد بود.
اما چرا به بردار نرمالسازیشده نیاز داریم؟ آیا نمیتوان از معیارهای سادهتر استفاده کرد؟ پاسخ این است که بردار نرمالشده، خواصی را که بالا گفته شد دارد و به همین دلیل باعث میشود معیار تولیدشده، همگِن بوده و نسبت به جابهجایی حساس نباشد.
فاصله را میتوان با استفاده از این فرمول محاسبه کرد:
فاصله مینکفسکی یک معیار تعمیمیافته است؛ منظور از تعمیمیافته این است که فرمول بالا را میتوان برای محاسبه فاصله بین دو نقطهداده، از جهات مختلف، استفاده کرد.
همانطور که پیشتر گفته شد، با دستکاری مقدار p میتوان فاصله را از سه طریق اندازهگیری کرد:
P=1؛ فاصله منهتن
P=2؛ فاصله اقلیدسی
P=∞؛ فاصله چبیشف
در این قسمت، این معیارهای فاصله را با جزئیات بیشتر توضیح خواهیم داد:
فاصله منهتن
هرگاه بخواهیم فاصله بین دو نقطهداده را در شبکهای همچون مسیر (خط) محاسبه کنیم، از معیار فاصله منهتن استفاده میکنیم. همانطور که پیشتر اشاره شد، برای محاسبه فاصله منهتن از فرمول فاصله مینکفسکی استفاده میکنیم و p را برابر با 1 قرار میدهیم.
فرض کنید میخواهیم d یعنی فاصله بین دو نقطه x و y را محاسبه کنیم:
همانطور که در فرمول پایین میبینید، d از جمع قدرمطلق تفاوت بین مختصات دکارتی دو نقطه به دست میآید:
در این فرمول، n تعداد متغیرها، xi و yi بردارهای (حدودی) x و y در فضای برداری دوبُعدی (برای مثال، x = (x1,x2,x3,…) و y = (y1,y2,y3,…)) را نشان میدهند.
پس فاصله d را میتوان بدین صورت محاسبه کرد:
(x1 – y1) + (x2 – y2) + (x3 – y3) + … + (xn – yn)
اینجا نحوه محاسبه این فاصله را به تصویر درآوردهایم:
فاصله منهتن را با عنوان Taxicab Geometry، City Block و… نیز میشناسند.
فاصله اقلیدسی
فاصله اقلیدسی یکی از پرکاربردترین معیارهای فاصله است. برای محاسبه این معیار، در فرمول فاصله مینکفسکی p را با 2 جایگذاری میکنیم. در نتیجه فرمول d بدین شکل در میآید:
همانطور که میبینید، این فرمول همان فرمول قضیه فیثاغورس است که پیشتر مرور کردیم.
فرمول فاصله اقلیدسی را میتوان برای محاسبه فاصله بین دو نقطهداده در یک صفحه استفاده کرد.
فاصله کسینوسی
معیار فاصله کسینوسی را اغلب برای پیدا کردن شباهت بین اسناد گوناگون استفاده میکنند. در معیار کسینوسی، اندازه زاویه بین دو سند/بردار (یعنی فراوانی جملات در اسناد مختلفی که بهعنوان معیار جمعآوری شدهاند) اندازهگیری میشود. زمانی این معیار را به کار میبریم که بزرگی زاویه بین بردارها اهمیتی نداشته باشد، بلکه جهت بردارها مهم باشد.
فرمول شباهت کسینوسی را میتوان از معادله مربوط به ضرب ماتریسی نقطهای به دست آورد:
سؤال اینجاست که معنی هر کدام از زوایای کسینوسی برای شباهت چیست:
بعد از مشخص کردن مقادیر لازم برای اندازهگیری شباهت، باید بدانیم 0، 1- و 1 نشاندهنده چه هستند.
مقدار کسینوسی 1 برای بردارهایی به دست میآید که در یک جهت قرار دارند، بدین معنی که بین اسناد/نقطهدادههای مدنظر شباهت وجود دارد. در واقع مقدار 0 نشان میدهد بردارها عمود بر هم هستند، یعنی ارتباطی بین آنها وجود ندارد (با این حال، مقداری شباهت وجود دارد). همچنین مقدار 1- حاکی از این است که بردارها در جهات مختلف قرار دارند و هیچ شباهتی بین آنها وجود ندارد.
فاصله ماهالانوبیس
برای محاسبه فاصله بین دو نقطهداده در یک فضای چندمتغیری از معیار فاصله ماهالانوبیس استفاده میشود.
بر اساس تعریف ویکیپدیا، فاصله ماهالانوبیس معیاری است برای اندازهگیری فاصله بین نقطه P و توزیع D. هدف از اندازهگیری این فاصله این است که دریابیم P چند انحراف معیار از میانگین توزیع D فاصله دارد.
مزیت استفاده از فاصله ماهالانوبیس این است که کوواریانس را هم مدنظر قرار میدهد؛ امری که به اندازهگیری قدرت/شباهت بین دو دادهی متفاوت، کمک میکند. فاصله بین یک مشاهده و میانگین توزیع را میتوان با این فرمول محاسبه کرد:
در این فرمول، S اندازه کوواریانس را نشان میدهد. هدف از معکوس کردن کوواریانس این است که معادله از نظر واریانس نرمالسازی شده باشد.
حال که تا حدی با معیارهای فاصله آشنا شدیم، تکنیکها و مدلهای یادگیری ماشینی را که از این معیارها استفاده میکنند، بررسی میکنیم.
معیارهای فاصله و مدلسازی یادگیری ماشینی
در این قسمت، روی مسائل مقدماتی و پایه ردهبندی و خوشهبندی تمرکز میکنیم، تا با نقش معیارهای فاصله در مدلسازی یادگیری ماشینی آشنا شویم. بدین منظور، مقدمهای مختصر از الگوریتمهای نظارتشده و غیرنظارتشده ارائه میدهیم و سپس به سراغ مثالها میرویم.
ردهبندی
KNN (K همسایه نزدیک)
KNN یک الگوریتم یادگیری نظارتشده و غیراحتمالی است. بدین معنی که احتمال تعلق هیچکدام از نمونهها را پیشبینی نمیکند، بلکه دادهها را بهصورت قطعی ردهبندی میکند؛ یعنی دادهها یا به کلاس 0 یا به کلاس 1 تعلق خواهند داشت. شاید از خود بپرسید اگر هیچ احتمالاتی در کار نباشد، KNN چطور کار میکند. KNN به منظور پیدا کردن شباهت یا تفاوت بین نمونهها از معیارهای فاصله استفاده میکند.
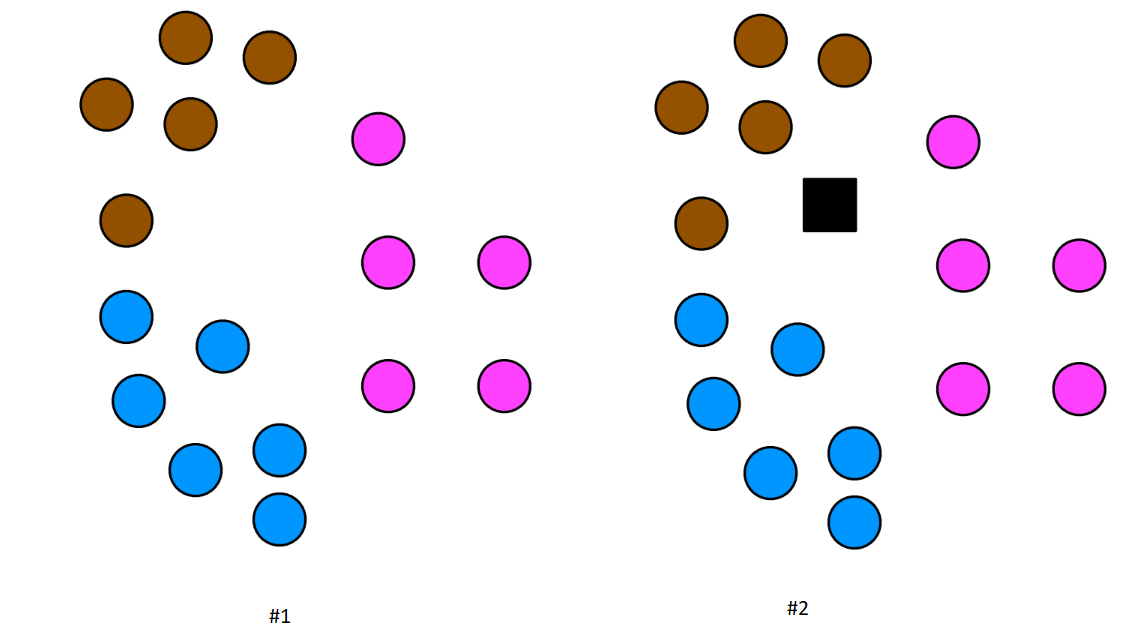
با استفاده از دیتاست iris که سه کلاس دارد، نحوه کارکرد KNN را در تشخیص کلاس دادههای آموزشی مشاهده میکنیم.
در تصویر دوم، مربع سیاهرنگ یک نقطهداده آزمایشی است. باید به کمک الگوریتم KNN دریابیم این نقطهداده آزمایشی در کدام کلاس قرار میگیرد. اکنون بهمنظور پیشبینی دادههای آزمایشی، دیتاست را آماده میکنیم:
#Import required libraries#Import required librariesimport numpy as np import pandas as pd from sklearn.model_selection import train_test_split from sklearn.neighbors import KNeighborsClassifier from sklearn.metrics import accuracy_score#Load the dataset url = "https://raw.githubusercontent.com/SharmaNatasha/Machine-Learning-using-Python/master/Datasets/IRIS.csv" df = pd.read_csv(url)#quick look into the data df.head(5)#Separate data and label x = df.iloc[:,1:4] y = df.iloc[:,4]#Prepare data for classification process x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3, random_state=0)
در الگوریتم ردهبندی KNN، مقدار ثابت K را تعریف میکنیم؛ K تعداد نزدیکترین همسایههای یک نقطهداده آزمایشی است. برای انتخاب کلاس نقطهداده آزمایشی از این K نقطهداده استفاده میشود (باید توجه کنید که K مربوط به دیتاست آموزشی است).
نقش معیار فاصله در پیدا کردن نزدیکترین همسایههاست. ابتدا فاصله بین هر نقطهداده آموزشی و آزمایشی را محاسبه میکنیم و سپس نزدیکترین نقاط (یعنی آنهایی که با توجه به مقدار K بالاترین مقدار فاصله را به دست آوردهاند) را انتخاب میکنیم.
نیازی نیست الگوریتم KNN را از ابتدا تولید کنیم؛ بلکه میتوانیم از کلسیفایر KNN کتابخانه scikit استفاده کنیم:
#Create a modelKNN_Classifier = KNeighborsClassifier(n_neighbors = 6, p = 2, metric='minkowski')
همانطور که در تصویر بالا مشاهده میکنید، از معیار فاصله مینکوفسکی با مقدار p=2 استفاده میکنیم؛ بدین معنی که کلسیفایر KNN از فرمول معیار فاصله اقلیدسی استفاده خواهد کرد.
سپس میتوان مدل را آموزش داده و پیشبینی کلاس دادههای آزمایشی را آغاز کرد.
بعد از اینکه نزدیکترین همسایهها انتخاب شدند، کلاسی که بیشترین رأی را در بین همسایگان دریافت کرده، مشخص میکنیم:
#Train the model KNN_Classifier.fit(x_train, y_train)#Let's predict the classes for test data pred_test = KNN_Classifier.predict(x_test)
آیا میتوانید با توجه به تصویر بالا کلاس نقطهداده آزمایشی را حدس بزنید؟ بله! این نمونه مربوط به کلاس 1 است، چون این کلاس بیشترین رأی را به دست آورده است.
با همین مثال کوچک، اهمیت معیار فاصله برای کلسیفایر KNN و دلیل آن را دریافتیم. این معیار به ما کمک کرد نزدیکترین نقطهدادههای آموزشی (که کلاسشان مشخص بود) را تعیین کنیم. احتمال این وجود دارد که استفاده از معیارهای فاصله دیگر، عملکرد مدل را بهبود بخشد. در کل میتوان گفت در الگوریتمهای غیراحتمالی همچون KNN، معیار فاصله نقش بسیار مهمی ایفا میکند.
خوشهبندی
K میانگین
در الگوریتمهای ردهبندی، چه احتمالی چه غیراحتمالی، به دادههای برچسبدار دسترسی داریم؛ بنابراین پیشبینی کلاس کار آسانتری است. با این حال، در الگوریتمهای خوشهبندی اطلاعاتی در مورد اینکه دادهها متعلق به کدام کلاس هستند نداریم. معیارهای فاصله جزء بسیار مهمی از این الگوریتم هستند.
در الگوریتم K میانگین، تعداد مراکز خوشه را تعیین میکنیم؛ این تعداد، شمار خوشهها را مشخص میکند. سپس هر نقطهداده به نزدیکترین مرکز (که با استفاده از معیار فاصله اقلیدسی مشخص میشود) اختصاص داده میشود. برای توضیح فرایند زیربنایی الگوریتم K میانگین از دیتاست iris استفاده میکنیم.
در تصویر بالا، شکل 1 جایگذاری تصادفی مراکز خوشه و شکل 2 پیدا کردن نزدیکترین خوشه با استفاده از معیار فاصله را نشان میدهد.
import numpy as np import pandas as pd from sklearn.cluster import KMeans import matplotlib.pyplot as plt#Load the dataset url = "https://raw.githubusercontent.com/SharmaNatasha/Machine-Learning-using-Python/master/Datasets/IRIS.csv" df = pd.read_csv(url)#quick look into the data df.head(5)#Separate data and label x = df.iloc[:,1:4].values#Creating the kmeans classifier KMeans_Cluster = KMeans(n_clusters = 3) y_class = KMeans_Cluster.fit_predict(x)
باید انتساب نمونهها به مراکز خوشهها را ادامه دهیم، تا زمانی که به یک ساختار خوشهای واضح دست یابیم.
همانطور که در مثال بالا مشاهده کردید، در الگوریتم خوشهبندی K میانگین، بدون در دست داشتن هیچ دانشی در خصوص برچسبها توانستیم دادهها را به سه کلاس تقسیم کنیم.
پردازش زبان طبیعی
بازیابی اطلاعات
در بازیابی اطلاعات با دادههای بدون ساختار سروکار داریم. دادهها میتوانند یک مقاله، وبسایت، ایمیل، پیامک، پستی در شبکههای اجتماعی و مواردی از این دست باشند. به کمک تکنیکهای بهکاررفته در حوزه پردازش زبان طبیعی، میتوانیم دادههای برداری ایجاد کنیم که در صورت ایجاد کوئری، برای بازیابی اطلاعات استفاده میشوند. بعد از اینکه دادههای بدون ساختار به شکل بردار در میآیند، میتوانیم از معیار شباهت کسینوسی استفاده کنیم، تا اسناد غیرمرتبط را از بدنه داده (متن) خارج کنیم.
با استفاده از یک مثال، کاربرد معیار شباهت کسینوسی را توضیح میدهیم:
1. ایجاد بردار از بدنه و کوئری
import math import numpy as np import pandas as pd import matplotlib.pyplot as pyplot from sklearn.metrics.pairwise import cosine_similarity from sklearn.feature_extraction.text import TfidfVectorizervectorizer = TfidfVectorizer()corpus = [ 'the brown fox jumped over the brown dog', 'the quick brown fox', 'the brown brown dog', 'the fox ate the dog' ]query = ["brown"]X = vectorizer.fit_transform(corpus) Y = vectorizer.transform(query)
2. بررسی شباهتها (پیدا کردن اسناد موجود در بدنه که به کوئری مرتبط هستند)
cosine_similarity(Y, X.toarray())Results: array([[0.54267123, 0.44181486, 0.84003859, 0. ]])
همانطور که در مثال بالا مشاهده میکنید، کلمه brown را بهعنوان کوئری مطرح کردیم و در کل بدنه، تنها 3 سند بودند که این شامل این کلمه میشدند. با استفاده از معیار شباهت کسینوسی نیز نتیجه مشابهی به دست میآید، یعنی سه سند (به جز سند چهارم) مقداری بزرگتر از 0 میگیرند.
جمعبندی
در این نوشتار، چند معیار شباهت/فاصله محبوب را مورد بررسی قرار دادیم و توضیح دادیم که این معیارها چطور میتوانند برای حل مسائل پیچیده یادگیری ماشینی به کار روند.