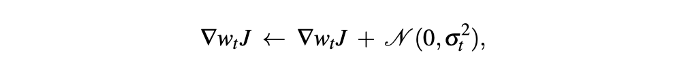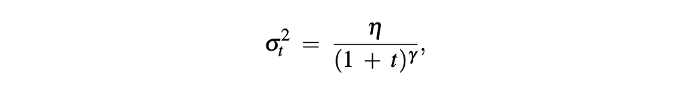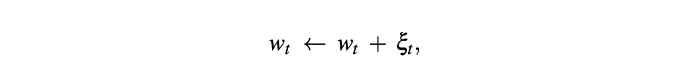نظریه جایگشت در آموزش شبکه عصبی عمیق، گرادیان کاهشی، نقطهی زینی
این مطلب فرض را بر آشنایی مقدماتی مخاطبان با معماری شبکه های عصبی قرار داده است. محتوای این مقاله درباره نظریه جایگشت است و به خصوص برای افرادی مفید است که در آموزش شبکههای عمیق تجربه دارند، و ممکن است در مورد آموزش مدل یا قدرت آن به مشکلاتی برخورده باشند.

یک جایگشت یا تغییر کوچک در مؤلفهها/پارامترهای مرتبط با آموزش (همچون گرادیانها، وزنها، ورودیها و غیره) میتواند بر آموزش DNN تأثیرگذار باشد و به غلبه بر مشکلات احتمالی، همچون مسئله گردایانهای کاهشی، تله saddle point یا خلق یک مدل قوی با استفاده از آموزش تخاصمی برای دوری از حملات مخرب، کمک کند.
نظریه جایگشت را میتوان مطالعه تغییری کوچک در یک سیستم دانست که میتواند حاصل تعامل یک شیء سوم با سیستم باشد. برای نمونه، حرکت یک شیء آسمانی (سیاره، ماه یا …) در اطراف خورشید را در نظر بگیرید؛ با اینکه خورشید با عظمت فراوانش 99.8% منظومه شمسی را در برمیگیرد، حرکت آن شیء از سایر سیارات/ماهها تأثیر میپذیرد. در آموزش شبکه DNN نیز میتوان از یک جایگشت کوچک در مؤلفهها (گردایانها، وزنها، ورودیها و …) برای حل مسائلی استفاده کرد که طی آموزش مدل یا استفاده از یک مدل آموزشدیده با آنها روبرو میشویم.
لازم به ذکر است نظریهای به نام جایگشت رسماً در حوزه یادگیری عمیق/ یادگیری ماشین وجود ندارد. با این حال در ادبیات این حوزه از اصطلاح «جایگشت» استفاده شده و اغلب به تغییری کوچک در یکی از مؤلفههای تشکیلدهنده شیء اشاره دارد. این مقاله حاصل جمعآوری و خلاصهسازی تکنیکهای مرتبط با جایگشت است که در پیشینه پژوهش مطرح شدهاند.
گرادیان کاهشی
شبکه عصبی روشی برای برآورد تابعی است که یک ورودی گرفته و یک خروجی تولید میکند. زیربنای این شبکه یک مدل جعبه سیاه آموزشدیده است که از تعداد زیادی تابع (f(g(x))) تشکیل شده است. هرکدام از لایههای نهان این مدل نماینده یک تابع در کل مجموعه است که به دنبال آنها یک تابع فعالسازی غیرخطی و سپس یک لایه نهان دیگر میآید. وظیفه تابع فعالسازی غیرخطی، ایجاد خروجی غیرخطی است؛ این تابع صرفاً مجموعهای از ضرایب ماتریسی است که میتوانند در یک ماتریس خلاصه شوند. این ماتریس فقط میتواند توابع خطی را مدلسازی کند و برای این کار تنها وجود یک لایه کافی است.
پارامترهای شبکه عصبی (وزنها و بایاس ها) با استفاده از یک مجموعه مقادیر اولیه مقداردهی میشوند. سپس بر اساس دادههای آموزشی به روزرسانی میشوند. به روزرسانی با استفاده از گرادیانهایی با جهت نزولی (کاهشی) برای پیدا کردن کمینه (minima) اجرا میشود (بهتر است بگوییم کمینه محلی، زیرا تابع غیرپیچشی است و تضمینی برای رسیدن به بهینه سراسری وجود ندارد)؛ این کارکرد فارغ از میزان پیچیدگی یا تعداد لایههای شبکه انجام میشود.
برای محاسبه گرادیان، از پارامترهای لایه آخر شروع میکنیم و سپس در جهت پسانتشار Back-propagation را تا لایههای اولیه انجام میدهیم. با حرکت از لایه آخر به لایههای اول، تعداد جملات ضربشده در محاسبه گرادیان برای پارامترهای هر لایه افزایش مییابد (گرادیان مجموعهای از توابع). ضرب این جملات زیاد میتواند باعث کاهش (ناپدید شدن) گرادیان برای لایههای ابتدایی شود (هرچه تعداد جملات افزایش یابد، عمق شبکه نیز بیشتر میشود)، زیرا این جملات در بازه بین [0,1] پارامترهای لایه اول قرار دارند که بازه تغییرات توابع فعال سازی است (برای نمونه تابع سیگموئید (0, 1/4)، تانژانت (0, 1) و غیره). به عبارت دیگر در گرادیان کاهشی، پارامترهای لایه آخر یادگیری خوبی دارند، اما هرچه به لایههای اولی نزدیکتر میشویم، گرادیانها شروع به ناپدید شدن میکنند یا آنقدر کاهش مییابند که زمان آموزش را تا حد چشمگیری افزایش میدهند. برای جلوگیری از این مشکل میتوان از تابع ReLU یا نسخههای دیگر آن، و یا از نرمالسازی بستهداده استفاده کرد. ما در این نوشتار توضیح خواهیم داد که جایگشتی کوچک در گرادیان میتواند در کمرنگتر کردن این مسئله مفید باشد (با استفاده از مقاله نیلاکانتان و دستیاران، 2015).
جایگشت در گرادیانها با اضافه کردن نویزی با توزیع گوسیGaussian-distributed، میانگین صفر و واریانس کاهشی (که بهتر از واریانس ثابت است) انجام میشود. حتی زمانی که مقدار تابع هزینه (J) در حال نزدیک شدن به همگرایی است، داشتن جایگشت ثابت ایدهآل نیست. این فرآیند برای جلوگیری از بیشبرازش نیز مفید است و میتواند تابع زیان آموزش را کاهش دهد. این گردایان جایگشتیافته در گام زمانی آموزشی t بدین طریق محاسبه میشود:
در این معادله، واریانس کاهشی (σ) در گام زمانی آموزشی t از این راه به دست میآید:
در معادله بالا مقدار η (اتا) معمولاً 1 در نظر گرفته میشود (با این حال قابل تغییر است، مقدار آن باید بین صفر تا یک باشد)، و پارامتر γ نیز روی 0/55 تنظیم میشود.
توجه داشته باشید که این فرآیند باعث افزایش تصادفی بودن آموزش میشود و در نتیجه میتواند برای جلوگیری از فاز Plateau در ابتدای یادگیری مفید باشد.
نقطه زینی (Saddle Point)
نقطه زینی نقطهای ایستا در یک منحنی است که شکل منحنی در آن قسمت شبیه زین (زین اسب) است (شکل 2). برای مثال، در منحنی کمینهسازی تابع زیان، نقطه ایستایی که وقتی یکی از محورها ثابت است کمینه محلی باشد، و درغیر این صورت (ثابت نبودن محورها) بیشینه باشد، نقطه زینی محسوب میشود (برای توضیح بهتر، بدون از دست دادن تعمیم پذیری، فرض میکنیم این منحنی سهبُعدی است). با حرکت از نقطه زینی در جهت همه محورها، مقدار تابع افزایش مییابد، اما در جهت مخالف این مقدار کاهش مییابد. بنابراین، برای اینکه یک نقطه را به عنوان کمینه در نظر بگیریم، حرکت از آن نقطه به تمام جهات باید مقدار را افزایش دهد، و برای بیشینه نیز عکس این موضوع صدق میکند.
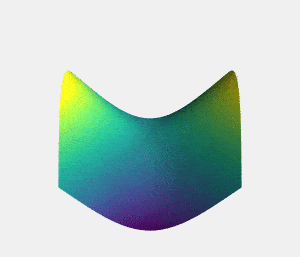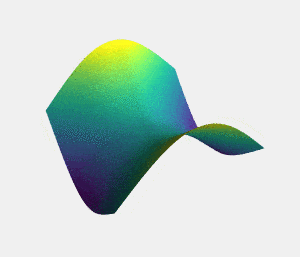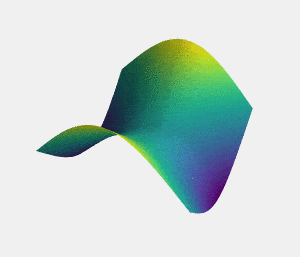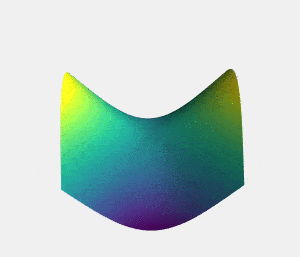
گاهی ممکن است فرآیند آموزشی در نقطه زینی گیر کند، زیرا گرادیان در این نقطه برابر با صفر است و این باعث میشود پارامترهای وزن (w) به روزرسانی نشوند. برای فرار از نقطه زینی میتوان در وزنها جایگشت انجام داد. جایگشت وزنها به گرادیان آنها بستگی دارد، برای مثال زمانی که مقدار نرمالسازی-L2 گرادیان کمتر از مقدار ثابت c است، میتوانید جایگشت را اجرا کنید. جایگشت از این طریق به دست میآید:
در این معادله wt وزن در دور آموزشی t است، و ξt به شکل یکسان از یک توپ نمونهگیری شده است که مرکز آن صفر و شعاع آن به اندازه کافی کوچک است. با این حال اضافه کردن نویز یکسان ضروری نیست، بلکه میتوان از نویزی با توزیع گوسی استفاده کرد؛ با این وجود، این روش مزیت تجربی خاصی ندارد. نویز یکسان برای سهولت در تحلیل استفاده میشود. اما زمانی که گرادیان کوچک است، الزامی به اضافه کردن نویز وجود ندارد. انتخاب اینکه کجا و چطور در وزنها جایگشتی وارد کنیم بر عهده ماست (برای مثال یکی از انواع جایگشت، جایگشت تناوبی است که در هر چند تکرار و بدون شرط انجام میشود و الگوریتم زمانی چندجملهای Polynomial time guarantee دارد).
آموزش تخاصمی
تخاصمadversary در فرهنگ لغت به عنوان دشمن، حریف، یا نیرویی تعریف شده است که مخالفت یا حمله میکند. نمونه تخاصمی در مدل یادگیری عمیق نیز یک ورودی مخرب، هرز یا سمی است که میتواند مدل را فریب داده و باعث کژکارکردی شود، به صورتی که با درصد اطمینان بالا، خروجی اشتباهی پیشبینی کند.
برای مقاوم کردن یک شبکه عصبی در مقابل این نمونههای تخاصمی، گودفلا و همکارانش جایگشت ورودیها را پیشنهاد میکنند. جایگشت با جمع ورودی و مقدار علامتی گرادیان (که با توجه به ورودی آموزشی محاسبه میشود) و ضرب حاصل در یک مقدار ثابت، باعث تعدد در ورودیها میشود. بدین طریق میتوان یک تصویر جایگشتیافته تولید کرد:
در این معادله x ورودی آموزشی، xˆ تصویر جدید و جایگشتیافته، ∇x(J) گرادیان تابع زیان (J) با توجه به ورودی آموزشی x است، ϵ نیز یک مقدار ثابت از پیشتعیین شده است که باید آنقدر کوچک باشد که بتواند به وسیله یک ابزار ذخیرهسازی داده با دقت محدود از بین برود. خروجی تابع علامتی نیز در صورتی که ورودی مثبت باشد، 1 و در صورتی که ورودی صفر باشد، 1- است. این تکنیک تحت قوانین ایالات متحده ثبت شده است؛
آموزش شبکه با ورودیهای جایگشتیافته، به خاطر تعدد، توزیع ورودی را گسترده میکند. این امر مقاومت شبکه را در مقابل مواردی همچون ورودیهای مخرب افزایش میدهد و میتواند جلوی حمله پیکسلیPixel attack در یک مسئله ردهبندی تصویر را بگیرد.
نتیجهگیری
در این مقاله با کاربرد جایگشت در حل مسائل مختلف مرتبط با آموزش شبکههای عصبی یا شبکههای عصبی آموزشدیده آشنا شدیم. جایگشت را در سه مؤلفه (گرادیانها، وزنها و ورودیها) در ارتباط با آموزش شبکه عصبی و شبکه عصبی آموزشدیده مشاهده کردیم. جایگشت در گرادیانها برای حل مسئله گرادیانهای کاهشی به کار میرود، در وزنها برای فرار از نقطه زینی، و در ورودیها برای جلوگیری از حملات تخاصمی و مخرب. در کل میتوان گفت جایگشت به طرق مختلف نقش مهمی در قدرتمندسازی مدل در برابر بیثباتیها ایفا میکند؛ برای مثال میتواند از ایستادن در نقطه اتلاف درستیCorrectness wreckage point (شکل 1) جلوگیری کند، زیرا چنین موقعیتی با جایگشت (ورودی، وزن، گرادیان) آزمون میشود و نتیجه، رویکرد مدل را در برابر نقطه اتلاف درستی نشان میدهد.
در حال حاضر دانشی که از جایگشت داریم اصولاً مربوط به آزمایشاتی تجربی است که برای حل مسائل موجود به صورت شهودی طراحی شدهاند. برای اینکه ببینیم جایگشت مؤلفهای از فرآیند آموزش از نظر شهودی معنادار است یا خیر و سپس برای اعتبارسنجی تجربی آن باید آزمایشاتی انجام دهیم. در هر صورت، در آینده اطلاعات بیشتری در مورد نظریه جایگشت در یادگیری عمیق به دست خواهیم آورد که ممکن است به صورت نظری نیز مورد حمایت قرار گیرد.