معرفی معماری RegNet؛ ساده، سریع و قدرتمند

تیم تحریریه
۲۴ شهریور ۱۴۰۰

زمان مطالعه: 8 دقیقه

در مقاله پیش‌رو به بررسی معماری RegNet می‌پردازیم.

فهرست مقاله پنهان

1 مرحله اول – معماری مولد ResNet

1.1 مرحله دوم – ساخت مدل‌های جمعیتی AnyNet

1.2 مرحله سوم – ساخت مدل‌های RegNet – RegNetX و RegNetY

1.3 مرحله چهارم – پیاده‌سازی پای تورچ مدل‌های RegNetX/ RegNetY

مرحله اول – معماری مولد ResNet

در ابتدا ساختار کلی ResNet را بررسی می‌کنیم. بررسی کردن ساختار ResNet به ما کمک می‌کند مدل‌های AnyNet که در مقاله مذکور به آن‌ها اشاره شده را ایجاد کنیم.

معماری RegNet — تصویر 1 – معماری پایه ResNet

همان‌گونه که در تصویر 1 نشان داده شده، معماری ResNet از یک بلاک Stem، یک بلاک Layer و یک بلاک Head تشکیل شده است.

Stem

Stem از یک لایه پیچشی با stride=2 و سایز فیلتر 3، نرمال سازی دسته ای Batch Normalization (BN) و فعال ساز ReLU تشکیل شده است. تعداد فیلترهای خروجی بسته به الزمات (بلوک قرمز در تصویر 1) می‌تواند 32 یا 64 فیلتر باشد.

Layer

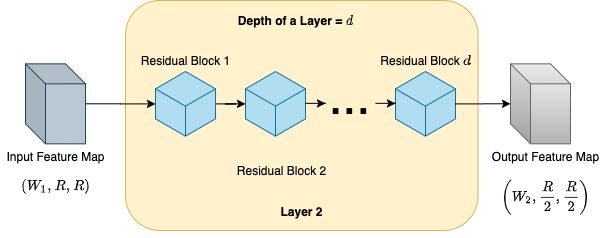
تصویر 2 – زنجیره بلوک‌های residual موجود در Layer Block ( بلوک زردرنگ در تصویر 1)

Layer Block شامل زنجیره‌ای از بلوک‌های residual است (بلوک آبی‌رنگ در تصویر 2). تعداد بلوک‌های موجود در یک لایه را با d (Depth یا همان عمق) نشان می‌دهیم. تعداد کانال‌های موجود در هر لایه در سرتاسر یک Layer Block ثابت باقی می‌ماند. تعداد کانال‌های موجود در هر لایه با w ( width یا همان پهنا) نشان داده می‌شود.
هر لایه یک نگاشت ویژگی W1×R×R را به عنوان ورودی دریافت می‌کند ( همان‌گونه که در تصویر 2 نشان داده شده است، اولین بلوک هر لایه کانال‌های W1 را به W2 تبدیل می‌کند و سپس تمامی بلوک‌ها همان تعداد کانال W2 را به عنوان خروجی ارائه می‌دهند) و همان‌گونه که در تصویر 2 نشان داده شده است نگاشت ویژگی W2×R/2×R/2 را به عنوان خروجی ارائه می‌دهد.
همان‌گونه که در تصویر مقابل نشان داده شده است، بلوک residual ( بلوک آبی در تصویر 2) ساختاری گلوگاه Bottleneck یا ساده خواهد داشت.

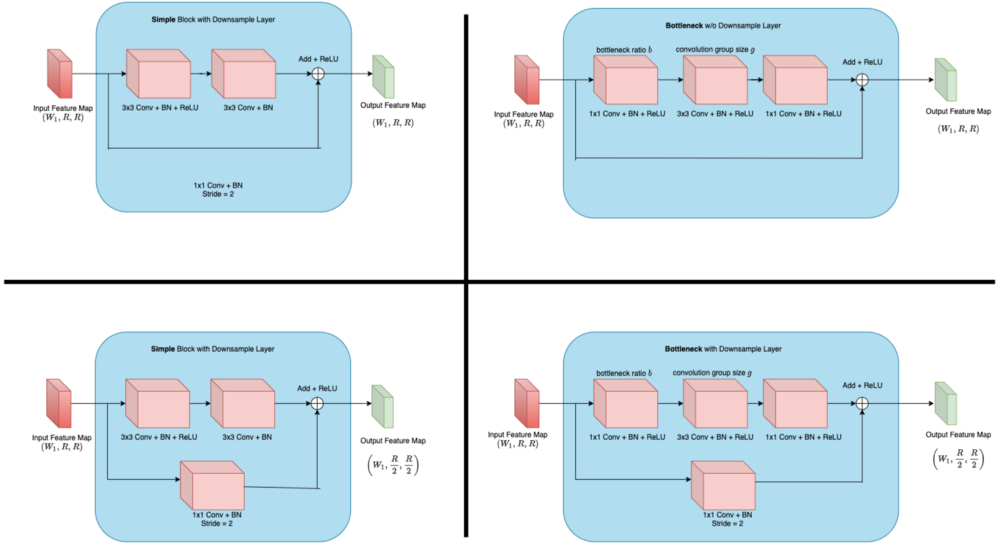
تصویر 3- نمایش ساختار ساده (سمت چپ) و گلوگاه (سمت راست) در تک تک بلوک‌های residual ( بلوک آبی در تصویر 2)

از ساختار کاهش نمونه داده شده Downsample فقط در اولین بلوک residual هر لایه استفاده می‌شود. و همان‌گونه که در تصویر 3 نشان داده شده است، ساختار سایر لایه‌ها گلوگاه خواهد بود.

نکته: با توجه به این‌که ساختار گلوگاه، معماری پایه AnyNet در نظر گرفته می‌شود، در ادامه این مقاله فقط به بررسی این ساختار می‌پردازیم.

همان‌گونه که در تصویر 3 نشان داده شده است، در این معماری از دو متغیر استفاده می‌شود. متغیر اول نسبت گلوگاه b است و متغیر دوم اندازه گروه پیچشی g است.
از متغیر نسبت گلوگاه به منظور کاهش تعداد کانال‌های نگاشت ویژگی ورودی استفاده می‌شود و از متغیر اندازه گروه برای پردازش گروهی پیچشی به صورت موازی استفاده می‌شود.

Head

Head شامل ساختاری ساده از AveragePool2D و یک لایه کامل متصل است. طبقه‌بندی مدل در این بخش اتفاق می‌افتد.

نکته: با تغییر پارامترهای d، w، نسبت گلوگاه b و اندازه گروه g می‌توان مدل‌های متفاوتی از AnyNet ساخت.

مرحله دوم – ساخت مدل‌های جمعیتی AnyNet

در این مرحله ساختار کلی AnyNet ساخته می‌شود.

نویسندگان مقاله طراحی فضاهای طراحی شبکه، از ساختار مولد معماری ResNet برای شناخت و طراحی جمعیت‌های مختلف مدل‌های AnyNet استفاده کرده‌اند.
با تغییر چهار پارامتری که در مرحله اول به آن‌ها اشاره شد می‌توانیم معماری‌های گوناگونی از AnyNet ایجاد کنیم. در ادامه فرایند پیکربندی پارامترها به همراه مقادیر ورودی توضیح داده شده است.

نویسندگان این مقاله در حوزه هوش مصنوعی از میان تمامی ترکیبات ممکن و با نمونه‌گیری یکنواخت Log uniform sampling از چهار پارامتر یادشده ، N ( = 500 در مقاله) مدل برای هر یک از خانواده‌های AnyNet ایجاد می‌کنند.

#Configuration input set for four different parameters.

Depth d = [1, 2, 3, 4, 5, ... , 16] #Total = 16
Width w = [8, 16, 24, ..., 1024] #Multiples of 8 <= 1024; Total=128
Bottleneck Ratio b: [1, 2, 4] #Total = 3
Group Size g: [1, 2, 4, 8, 16, 32] #Total = 6

مجموع درجه آزادی مدل‎های AnyNetX، 16 است (با استفاده از چهار پارامتر مذکور می‌توان در چهار لایه و هر لایه به صورت جداگانه تغییر ایجاد کرد).

در مقاله مذکور پنج مدل AnyNet معرفی شده است. در این قسمت هر یک از این مدل‌ها را به صورت جداگانه معرفی می‌کنیم.

AnyNetXA

AnyNetXA معماری مولد و بدون محدودیت ResNet است (مرحله اول) و تمامی مقادیر ممکن چهار پارامتر یادشده را شامل می‌شود.
مجموع ساختارهای ممکن در AnyNetXA برابر با ⁴( 6 * 3* 128* 16) است که به طور تقریبی برابر با 10¹⁸ساختار است.

AnyNetXB

برای ساخت مدل AnyNetXB می‌توانیم از مدل AnyNetXA زیر استفاده کنیم

b(Layer 1) =b(Layer 2) =b(Layer 3) =b(Layer 4)

مجموع ساختارهای ممکن در AnyNetXB برابر با 3* ⁴ (6 * 128 * 16) است که به طور تقریبی برابر با 10¹⁶است.

AnyNetXC

AnyNetXC را می‌توان با استفاده از AnyNetXB به صورت زیر ایجاد کنیم

g(Layer 1) =g(Layer 2) =g(Layer 3) =g(Layer 4)

تعداد کل ساختارهای ممکن در AnyNetXC برابر با 6* 3* ⁴(128 * 16) است که به طور تقریبی برابر با 10¹⁴ساختار است.

AnyNetXD

AnyNetXD را می‌توان با استفاده از AnyNetXC به صورت زیرساخت

w(Layer 1) ≤w(Layer 2) ≤w(Layer 3) ≤w(Layer 4).

تعداد کل ساختارهای ممکن در AnyNetXD برابر با 4/ 6 * 3 ⁴(128 * 16) است که به طور تقریبی برابر با 10¹³ساختار است.

AnyNetXE

AnyNetXE را می‌توان با استفاده از AnyNetXD به صورت زیر ایجاد کنیم

d(Layer 1) ≤ d(Layer 2) ≤ d(Layer3)≤d(Layer 4)(Not always for the last layer).

تعداد کل ساختارهای ممکن در AnyNetXE = (4) / 6 * 3 ⁴(128 * 16) است که به طور تقریبی برابر با 10¹¹ ساختار است.

نکته: با در نظر گرفتن یعضی از محدودیت ها، نویسندگان مقاله توانسته اند فضای طراحی را به O(10⁷) نسبت به مدل AnyNetXA model کاهش دهند.

مرحله سوم – ساخت مدل‌های RegNet – RegNetX و RegNetY

در این مرحله می‌توانیم معماری‌های RegNetX و RegNetY را ایجاد کنیم.

نویسندگان این مقاله از مدل‌های AnyNetXE برای ایجاد RegNetX و RegNetY استفاده کردند.
نویسندگان این مقاله پس از اعمال مقادیر مختلف به پارامترها و بررسی دقت آن‌ها متوجه ترندها و مجموعه‌ای از معادلات مشابه شدند که به یافتن بهترین مدل RegNetX با استفاده از ورودی پیکربندی‌هایی که به آن‌ها اشاره شده کمک می‌کند.

پهنای اولیه Degree of freedom w0: پهنای اولین لایه در معماری ResNet است.
پارامتر شیب Initial width wa: برای پیدا کردن روند خطی بهترین مدل‌ها استفاده می‌شود.
پارامتر کمی کردن Slope parameter wm: از این پارامتر برای کمی‌ کردن روند خطی استفاده می‌شود.
عمق شبکه D: مجموع عمق تمامی لایه‌ها di{ i= 1,2,3,4}
نسبت گروه و گلوگاه g و b

#Configuration Domain for RegNetX Model Input Parameters

Network Depth D = {1, 2, ..., 63} OR {12, 13, ..., 28} 
Slope Parameter wa = {0, 1, 2, ..., 255} 
Quantization Parameter wm = [1.5, 3]
Initial Width w0 > 0
Bottleneck Ratio b = 1
Group Width g = {1, 2, 4, 8, 16, 32} OR {16, 24, 32, 40, 48, 56, 64}

ایجاد مدل RegNetX

نکته: در این مطلب قصد داریم معماری RegNet را توضیح دهیم و به همین دلیل وارد جزئیات معادله نمی‌شویم.

برای تکمیل کردن معماری RegNet به عمق d و پهنای w هر چهار لایه نیاز داریم. چگونه می‌توانیم عمق و پهنای چهار لایه را به دست آوریم؟ عمق d و پهنا w را می‌توانیم با استفاده از سه معادله کوچک محاسبه کنیم.
با ذکر یک مثال کوچک مقادیر یادشده را محاسبه می‌کنیم.

#Input Parameters List

Network Depth D = 13
Slope Parameter wa = 36
Initial width w0 = 24
Quantization parameter wm = 2.5
Bottleneck ratio b = 1
Group Width g = 8

1- یافتن پهناهای u برای یک شیب مشخص wa و پارامتر پهنای اولیه w0.

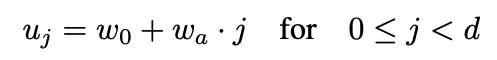
معادله 1. معادله پهناهای پارامترسازی‌شده

import numpy as np
u = w0 + wa * np.arange(D) # Equation 1
print(u)

# Output 
[ 24  60  96 132 168 204 240 276 312 348 384 420 456 492 528]

2- پیدا کردن اندازه احتمالی بلوک s بر اساس پهنای محاسبه شده u، پهنای اولیه w0 و پارامتر تدریجی‌شده Quantize wm.

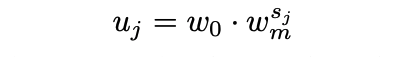
معادله 2. معادله بلوک‌های پارامتر‌سازی شده

s = np.log(u / w0) / np.log(wm) # Equation 2
print(s)

# Output
[ 0. 0.7564708 1.51294159 1.7564708 2.12368202 2.26941239
  2.51294159 2.61695899 2.79927458 2.88015281 3.02588319  3.09204627
  3.21343311  3.26941239  3.37342979]

3 – پیدا کردن پهناهای w کمی‌شده از طریق گِرد کردن Rounding اندازه‌های بلوک پارامتر‌سازی‌شده s. البته باید مطمئن شویم که پهناهای w تدریجی‌شده بر 8 تقسیم ‌پذیر هستند.

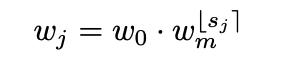
معادله 3. پهناهای w تدریجی‌شده از پهناهای u ممکن

s = np.round(s) #Rounding the possible block sizes s
w = w0 * np.power(wm, s) # Equation 3
w = np.round(w / 8) * 8 # Make all the width list divisible by 8
print(w)

#Output
[  24. 64. 152. 152. 152. 152. 376. 376. 376. 376. 376. 376.
  376. 376. 376.]

4 – پیدا کردن فهرست عمق d. برای پیدا کردن عمق d، تعداد دفعات وقوع هر یک از پهناهای w تدریجی‌شده را محاسبه می‌کنیم. برای محاسبه فهرست نهایی پهنای w، فقط از مقادیر منحصر به فرد استفاده می‌کنیم.

#Finding final width of depth list
w, d = np.unique(w.astype(np.int), return_counts=True)
print("Width list w: ", w)
print("Depth list d: ", d)

#Output
Width list w: [ 24 64 152 376]
Depth list d: [1 1 4 7]

5 – فهرست پهنای w ایجاد شده باید مضرب اندازه گروه g باشد. پهناهای ایجادشده ممکن است به دلیل نسبت گلوگاه b، مغایر باشند. برای تصحیح آن‌ها، مطابق مراحل زیر عمل کنید.

gtemp = np.minimum(g, w//b)

w = np.round(w // b / gtemp) * gtemp #To make all the width compatible with group sizes of the 3x3 convolutional layers

g = np.unique(gtemp * b)[0]

print("Revised width list w: ", w) 
print("Revised group size g: ", g)

#Output

Revised group size w: [24 64 152 376]
Revised group size g: 8

6 – فهرست نهایی پهناهای w و عمق d ایجاد شد. در این مرحله، مقادیر w، d، b و g را به معماری ResNet وارد می‌کنیم تا مدل ReNetX ایجاد شود.

همزمان با افزایش تعداد پهنا و عمق‌ها، مدت زمانی که مدل برای محاسبه نیاز دارد، نیز افزایش پیدا می‌کند. مدلی که ایجاد کردیم RegNetX 200MF است. منظور از 200MF، 200 میلیون عملیات ممیز شناور در ثانیه FLOPs است.
با مراجعه به مقاله اصلی می‌توانید RegNetX-ABC MF/ GF را مشاهده کنید.

ایجاد مدل RegNetY

تفاوت مدل RegNetX و RegNetY در این است که در مدل RegNetY یک لایه Squeeze و Excitation افزوده می‌شود. RegNetY = RegNetX + SE
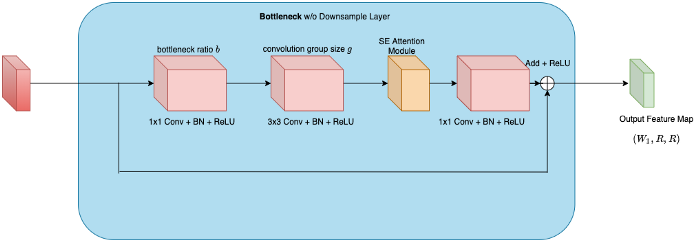
همان‌گونه که در تصویر مقابل نشان داده شده است، پس از هر لایه پیچشی 3×3 در بلوک residual معماری ResNet، ماژول توجه متصل می‌شود.

همزمان با افزایش تعداد پهنا و عمق‌ها، مدت زمانی که مدل برای محاسبه نیاز دارد، نیز افزایش پیدا می‌کند. مدلی که ایجاد کردیم RegNetX 200MF است. منظور از 200MF، 200 میلیون عملیات ممیز شناور در ثانیه است.
با مراجعه به مقاله اصلی می‌توانید RegNetX-ABC MF/ GF را مشاهده کنید.

ایجاد مدل RegNetY

تفاوت مدل RegNetX و RegNetY در این است که در مدل RegNetY یک لایه Squeeze و Excitation افزوده می‌شود. RegNetY = RegNetX + SE
همان‌گونه که در تصویر مقابل نشان داده شده است، پس از هر لایه پیچشی 3×3 در بلوک residual معماری ResNet، ماژول توجه متصل می‌شود.

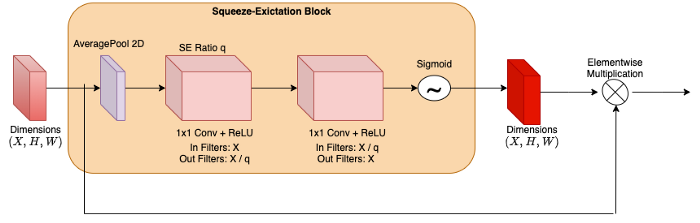
مراحل ایجاد RegNetY و RegNetX یکسان هستند. تنها تفاوت این دو معماری در این است که در RegNetY پارامتر جدید Se-ration q افزوده می‌شود. Range: 0 ≤ q ≤ 1.

مرحله چهارم – پیاده‌سازی پای تورچ مدل‌های RegNetX/ RegNetY

1	”’
2	Name: Shreejal Trivedi
3
4	Description: Generation Script of RegNetX and RegNetY models
5
6	References: Designing Network Design Spaces from Facebook AI March’2020
7
8	”’
9
10	#Importing Libraries
11	import torch
12	import torch.nn as nn
13	import torch.nn.functional as F
14	import numpy as np
15	import argparse
16
17	#Downsampling used in first bottleneck block of every layer in RegNet
18	class Downsample(nn.Module):
19	def __init__(self, in_filters, out_filters, stride):
20	super(Downsample, self).__init__()
21
22	self.conv1x1 = nn.Conv2d(in_filters, out_filters, kernel_size=1, stride=stride, bias=False)
23	self.bn = nn.BatchNorm2d(out_filters)
24
25	def forward(self, x):
26	return self.bn(self.conv1x1(x))
27
28
29	#SE Attention Module for RegNetY
30	class SqueezeExcitation(nn.Module):
31
32	def __init__(self, in_filters, se_ratio):
33	super(SqueezeExcitation, self).__init__()
34
35	#Calculate bottleneck SE filters
36	*out_filters = int(in_filters se_ratio)**
37
38	#Average Pooling Layer
39	self.avgpool = nn.AdaptiveAvgPool2d(output_size=1)
40
41	#Squeeze
42	self.conv1_1x1 = nn.Conv2d(in_filters, out_filters, kernel_size=1, bias=True)
43
44	# Excite
45	self.conv2_1x1 = nn.Conv2d(out_filters, in_filters, kernel_size=1, bias=True)
46
47	def forward(self, x):
48
49	out = self.avgpool(x)
50	out = F.relu(self.conv1_1x1(out))
51	out = self.conv2_1x1(out).sigmoid()
52	*out = x out**
53	return out
54
55	#Bottleneck Residual Block in Layer
56	class Bottleneck(nn.Module):
57	def __init__(self, in_filters, out_filters, bottleneck_ratio, group_size, stride=1, se_ratio=0):
58	super(Bottleneck, self).__init__()
59
60	#1×1 Bottleneck Convolution Block
61	bottleneck_filters = in_filters // bottleneck_ratio
62	self.conv1_1x1 = nn.Conv2d(in_filters, bottleneck_filters, kernel_size=1, bias=False)
63	self.bn1 = nn.BatchNorm2d(bottleneck_filters)
64
65	#3×3 Convolution Block with Group Convolutions —> ResNext alike structure
66	num_groups = bottleneck_filters // group_size
67	self.conv2_3x3 = nn.Conv2d(bottleneck_filters, bottleneck_filters, kernel_size=3, stride=stride, padding=1, groups=num_groups, bias=False)
68	self.bn2 = nn.BatchNorm2d(bottleneck_filters)
69
70	#Squeeze-Exictation Block: Only for RegNetY
71	self.se_module = SqueezeExcitation(bottleneck_filters, se_ratio) if se_ratio < 1 else None
72
73	#Downsample if stride=2
74	self.downsample = Downsample(in_filters, out_filters, stride) if stride != 1 or in_filters != out_filters else None
75
76	#1×1 Convolution Block
77	self.conv3_1x1 = nn.Conv2d(bottleneck_filters, out_filters, kernel_size=1, bias=False)
78	self.bn3 = nn.BatchNorm2d(out_filters)
79
80	def forward(self, x):
81	residual = x
82
83	out = F.relu(self.bn1(self.conv1_1x1(x)))
84	out = F.relu(self.bn2(self.conv2_3x3(out)))
85
86	if self.se_module is not None:
87	out = self.se_module(out)
88
89	out = self.bn3(self.conv3_1x1(out))
90
91	if self.downsample is not None:
92	residual = self.downsample(x)
93
94	out += residual
95	out = F.relu(out)
96
97	return out
98
99	class Stem(nn.Module):
100	def __init__(self, out_filters, in_filters=3):
101	super(Stem, self).__init__()
102
103	self.conv3x3 = nn.Conv2d(in_filters, out_filters, kernel_size=3, stride=2, padding=1, bias=False)
104	self.bn = nn.BatchNorm2d(out_filters)
105
106	def forward(self, x):
107	return F.relu(self.bn(self.conv3x3(x)))
108
109	class Layer(nn.Module):
110	def __init__(self, in_filters, depth, width, bottleneck_ratio, group_size, se_ratio):
111	super(Layer, self).__init__()
112
113	self.layers = []
114
115	#Total bottleneck blocks in a layer = Depth d
116	for i in range(depth):
117	stride = 2 if i == 0 else 1
118	bottleneck = Bottleneck(in_filters, width, bottleneck_ratio, group_size, stride, se_ratio)
119	self.layers.append(bottleneck)
120	in_filters = width
121
122	*self.layers = nn.Sequential(self.layers)**
123
124	def forward(self, x):
125	out = self.layers(x)
126	return out
127
128	class Head(nn.Module):
129
130	def __init__(self, in_filters, classes):
131
132	super(Head, self).__init__()
133
134	self.avgpool = nn.AdaptiveAvgPool2d(output_size=1)
135	self.fc = nn.Linear(in_filters, classes)
136
137
138	def forward(self, x):
139
140	out = self.avgpool(x)
141	out = torch.flatten(out, 1)
142	out = self.fc(out)
143	return out
144
145	class RegNet(nn.Module):
146	def __init__(self, paramaters, classes=2):
147	super(RegNet, self).__init__()
148
149	#Model paramater initialization
150	self.in_filters = 32
151	self.w, self.d, self.b, self.g, self.se_ratio = parameters
152	self.num_layers = 4
153
154	#Stem Part of the generic ResNet/ResNeXt architecture
155	self.stem = Stem(self.in_filters)
156	self.body = []
157
158	for i in range(self.num_layers):
159	layer = Layer(self.in_filters, self.d[i], self.w[i], self.b, self.g, self.se_ratio)
160	self.body.append(layer)
161	self.in_filters = self.w[i]
162
163	#Body Part: Four Layers containing bottleneck residual blocks
164	*self.body = nn.Sequential(self.body)**
165
166	#Head Part: Classification Step FC + AveragePool
167	self.head = Head(self.w[-1], classes)
168
169	def forward(self, x):
170
171	out = self.stem(x)
172	out = self.body(out)
173	out = self.head(out)
174	return out
175
176	def generate_parameters_regnet(D, w0, wa, wm, b, g, q):
177
178	*u = w0 + wa np.arange(D) # Equation 1**
179	s = np.log(u / w0) / np.log(wm) # Equation 2
180
181	s = np.round(s) #Rounding the possible block sizes s
182	*w = w0 np.power(wm, s) # Equation 3**
183	*w = np.round(w / 8) 8 # Make all the width list divisible by 8**
184
185	w, d = np.unique(w.astype(np.int), return_counts=True) #Finding depth and width lists.
186
187	gtemp = np.minimum(g, w//b)
188	*w = (np.round(w // b / gtemp) gtemp).astype(int) #To make all the width compatible with group sizes of the 3×3 convolutional layers**
189	g = np.unique(gtemp // b)[0]
190
191	return (w, d, b, g, q)
192
193	if __name__ == ‘__main__’:
194
195	parser = argparse.ArgumentParser(description=”RegNetX \| RegNetY Models Generation”)
196
197	parser.add_argument(‘-D’, default=13, type=int, help=’Network Depth: Range::[12, 13, …, 28]’)
198	parser.add_argument(‘-w0′, default=24, type=int, help=’Initial Width of the First Layer > 0’)
199	parser.add_argument(‘-wa’, default=36, type=int, help=’Slope Parameter: Range::[0, 1, 2, …, 255]’)
200	parser.add_argument(‘-wm’, default=2.5, type=float, help=’Quantization Parameter: Range::[1.5, 3]’)
201	parser.add_argument(‘-b’, default=1, type=int, help=’Bottleneck Ratio: Range::{1, 2, 4}’)
202	parser.add_argument(‘-g’, default=8, type=int, help=’Group Size: Range::{1, 2, 4, 8, 16, 32} OR {16, 24, 32, 40, 48, 56, 64}’)
203	parser.add_argument(‘-q’, default=1, type=float, help=’0 <= SE Ratio < 1′)
204	args = parser.parse_args()
205
206	parameters = generate_parameters_regnet(args.D, args.w0, args.wa, args.wm, args.b, args.g, args.q)
207	model = RegNet(parameters)