
توضیح بهینه سازی بیزی به بیان ساده
در این مقاله بهینه سازی بیزی را توضیح خواهیم داد. فرض کنید این تابع را به ما دادهاند: f(x). محاسبه آن هزینهبر است، نمیتوان آن را یک عبارت تحلیلی Analytic expression در نظر گرفت و مشتقهای آن هم ناشناخته هستند.
مسئلهای که باید حل کنید این است که کمینه سراسری Global minima این تابع را پیدا کنید.
این مسئله از سایر مسائل بهینهسازی در حوزهی یادگیری ماشین دشوارتر است. برای مثال، روشی همچون گرادیان کاهشی به مشتقهای تابع دسترسی دارد و به همین دلیل میتواند با استفاده از میانبرهای ریاضیاتی، عبارات را سریعتر ارزیابی کند.
ارزیابی تابع برای بهینهسازی همیشه کار هزینهبری نیست؛ اگر بتوانیم صدها نتیجه برای مشتقات ورودی x را طی چند ثانیه به دست آوریم، میتوانیم با انجام یک جستجوی شبکهای ساده، به نتایج خوب و قابل قبولی دست پیدا کنیم.
گاهی اوقات نیز میتوان از انواع روشهای بهینهسازی غیرسنتی و غیرگرادیانی، همچون بهینهسازی ازدحام ذرات Particle swarming یا تبرید شبیهسازی شده Simulated annealing، استفاده کرد.
متأسفانه، در مسئلهای که در دست داریم نمیتوانیم از هیچکدام این امکانات استفاده کنیم. به عبارتی برای بهینهسازی، از چندین لحاظ با محدودیت روبرو هستیم؛ از جمله این محدودیتها میتوان به این موارد اشاره کرد:
- محاسبات هزینهبر: در حالت ایدهآل میتوان تابع را آنقدر فراخواند تا به دفعات لازم تکرار شود، اما در این روش بهینهسازی، باید طی چند بار نمونهگیری محدود از ورودیها به نتیجه رسید؛
- ناشناخته بودن مشتق: بیدلیل نیست که گرادیان کاهشی و روشهای برگرفته از آن همچنان جزو محبوبترین روشهای یادگیری عمیق و گاهی حتی یادگیری ماشین به شمار میروند. با دانستن مشتقات میتوان به بهینهساز جهت داد و ما در این مسئله به این مورد دسترسی نداریم؛
- کمینهی سراسری: در این مسئله باید کمینهی سراسری را پیدا کنیم؛ مسئلهای که حتی با استفاده از روش پیچیدهای همچون گرادیان کاهشی نیز دشوار است. پس مدل ما باید مکانیزمی داشته باشد تا از گیر افتادن در کمینههای محلی خودداری کند.
راهکار پیشنهادی: بهینه سازی بیزی Bayesian optimization، چارچوبی بینظیر است که برای چنین مسائلی راهحل مناسبی ارائه میدهد و باعث میشود در حداقل گامهای ممکن به کمینهی سراسری برسیم.
برای مثال، تابع c(x) را میسازیم؛ c(x) تابع هزینه یک مدل با ورودی x است. البته بهینهساز، شکل تابع که در تصویر پایین مشخص شده را نمیداند. این تابع را تابع هدف میخوانیم.
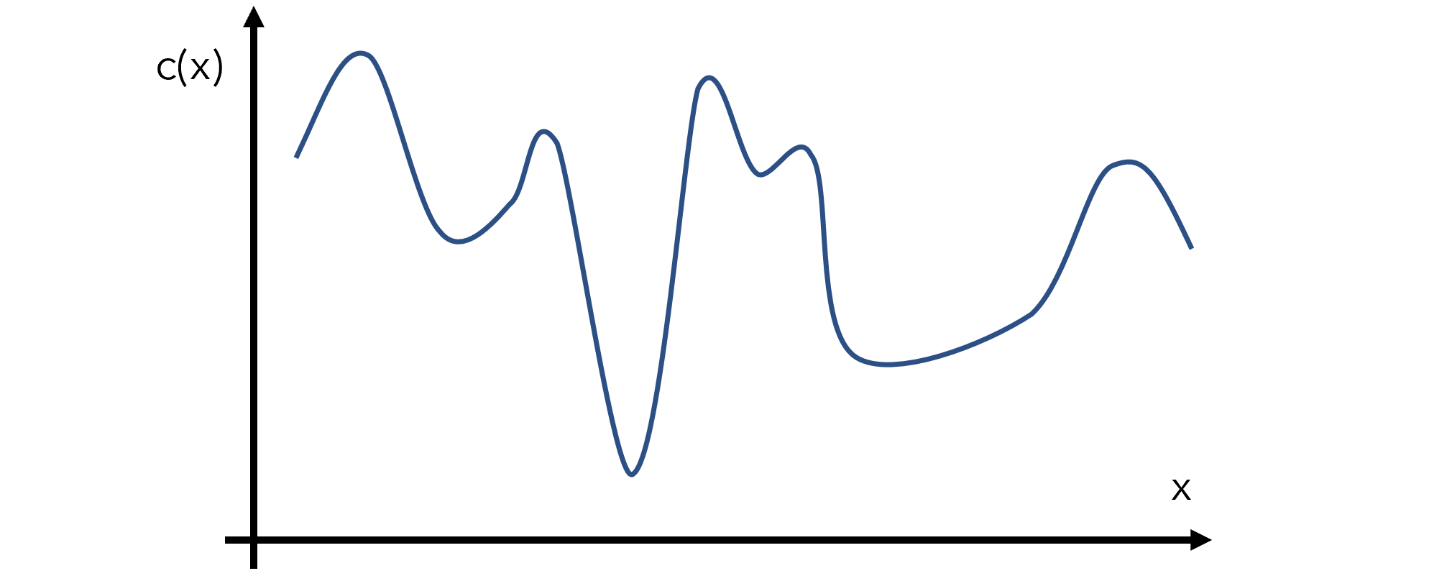
رویکردهای بهینه سازی بیزی چنین مسئلهای را با روشی به نام بهینهسازی جایگزین Surrogate optimization حل میکنند. برای اینکه درک بهتری از دلیل نامگذاری این روش پیدا کنید، یادآوری میکنیم که مادر جایگزین Surrogate mother به خانمی گفته میشود که قبول میکند فرزند فرد دیگری را به دنیا بیاورد. تابع جایگزین را نیز به همین شکل، میتوان برآوردی از تابع هدف دانست.
تابع جایگزین بر اساس نقاط نمونهگیری شده از تابع اصلی ایجاد میشود.
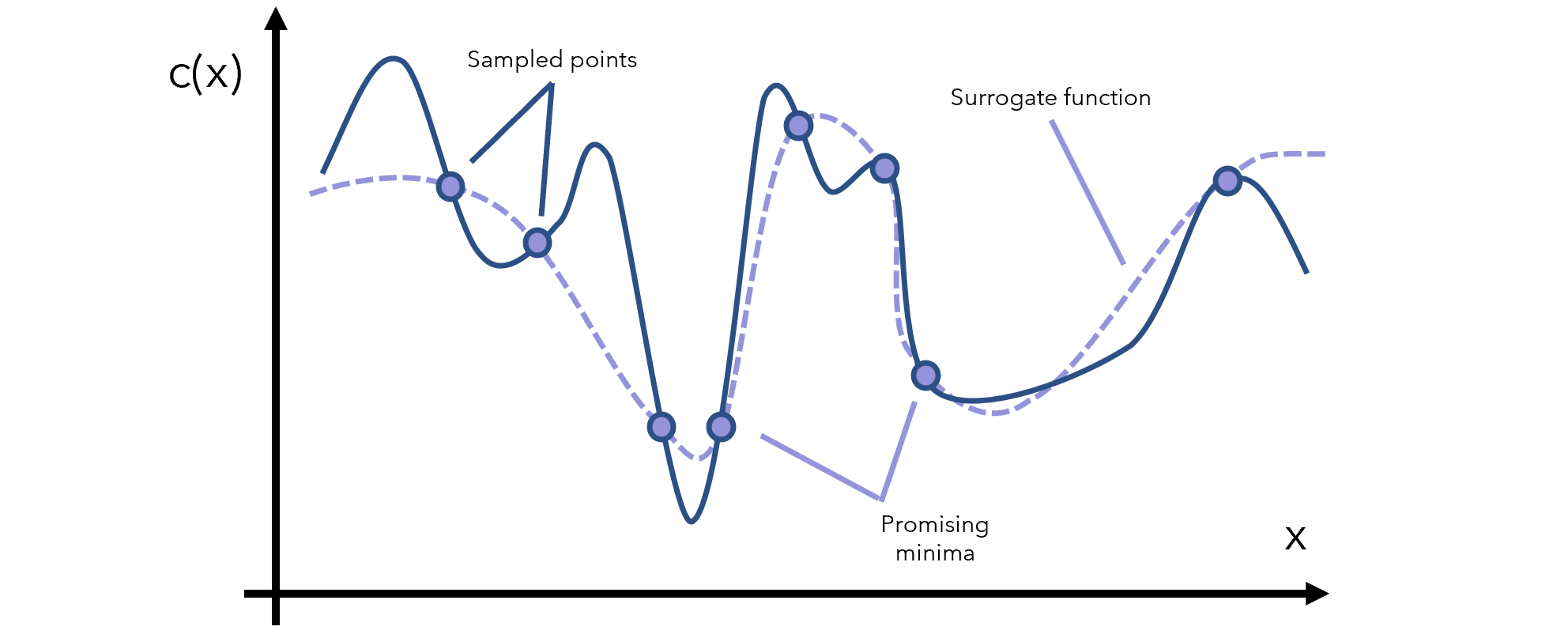
به کمک تابع جایگزین تشخیص میدهیم کدام نقاط میتوانند کمینه باشند؛ بنابراین از این نواحی امیدوارکننده، نمونهگیری بیشتری انجام میدهیم و تابع جایگزین را بر همین اساس بروز رسانی میکنیم.
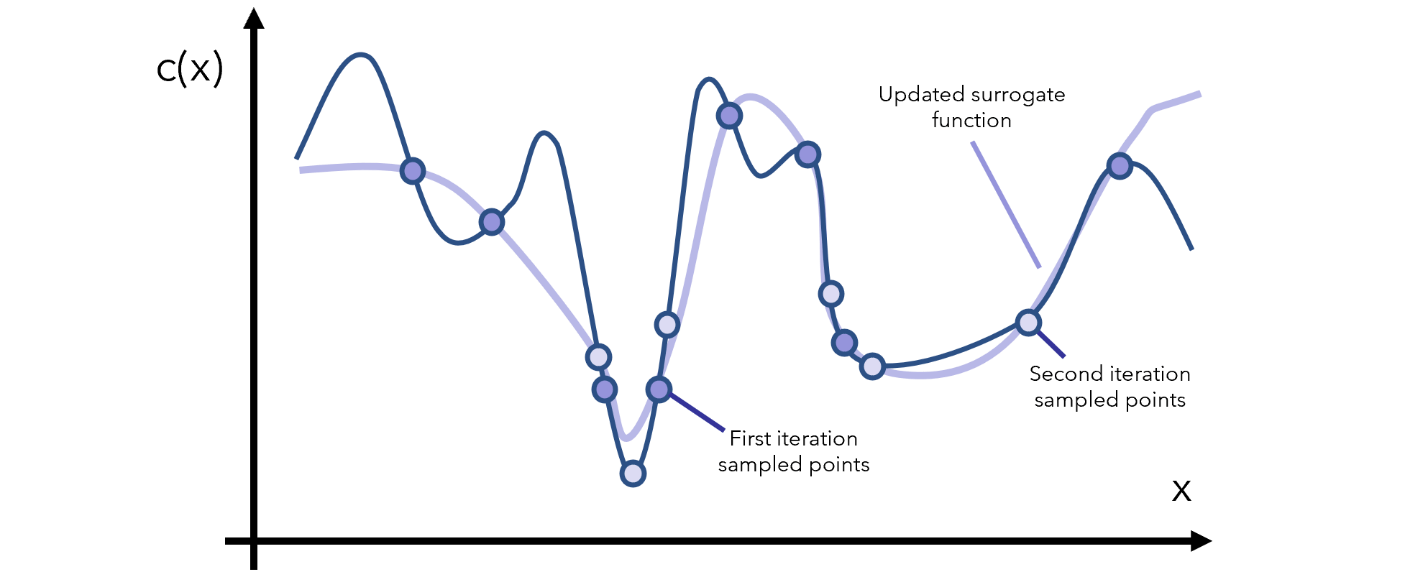
طی هر بار تکرار، به تابع جایگزین موجود نگاه میکنیم و با نواحی که باید نمونهگیری بیشتری از آنها انجام شود بیشتر آشنا میشویم. نکته اینجاست که تابع جایگزین از نظر ریاضیاتی به شکلی است که ارزیابی آن بسیار ارزانتر از ارزیابی تابع هدف خواهد بود؛ برای مثال، تابع y=x در یک بازهی مشخص، برآوردی کمهزینهتر از تابع پیچیدهتری همچون y=arcsin((1-cos²x)/sin x) است.
بعد از چند دور تکرار به کمینهی محلی دست خواهیم یافت، مگر اینکه شکل تابع خیلی عجیب باشد (به صورتی که نوسانات بسیار شدید و بزرگی داشته باشد). در این صورت، سؤالی که باید از خود بپرسید این است که «دادههایتان چه مشکلی دارند؟»
شاید بتوان گفت زیبایی این رویکرد در این است که به هیچ مفروضهای در مورد تابع نیاز ندارد (به غیر از اینکه اصلاً قابلیت بهینه شدن داشته باشد)؛ نیازی به اطلاعات در مورد مشتقات تابع ندارد، و میتواند با استفاده از یک برآورد از تابع اصلی که به صورت پیوسته به روز رسانی میشود، از استدلالی منطقی استفاده کند. با این رویکرد، ارزیابی پرهزینهی تابع اصلی دیگر مشکلی به شمار نمیرود.
آنچه تا اینجا توضیح دادیم رویکردی مبتنی بر جایگزین بود؛ شاید از خود بپرسید چه چیزی آن را در شمار روشهای بیزی قرار میدهد؟
اساس آمار و مدلهای بیزی، به روزرسانی دانش پیشین با استفاده از اطلاعات جدید، به منظور تولید دانش پسین است. از آنجایی که بهینهسازی جایگزین هم دقیقاً همین کار را انجام میدهد، بهتر است آن را در قالب سیستمها، فرمولها و ایدههای بیزی در نظر بگیریم.
اجازه دهید تابع جایگزین را با دقت بیشتری مورد بررسی قرار دهیم. توابع جایگزین معمولاً از طریق فرآیندهای گاوسی بازنمایی میشوند. این فرآیندها را میتوان مثل انداختن تاس در نظر گرفت، با این تفاوت که نتیجهی آن به جای عددی از 1 تا 6، توابعی متناسب با نقطهدادههاست (برای مثال تابع سینوسی، لگاریتمی و غیره). بنابراین، خروجی این فرآیند چندین تابع است که هرکدام احتمالاتی دارند.
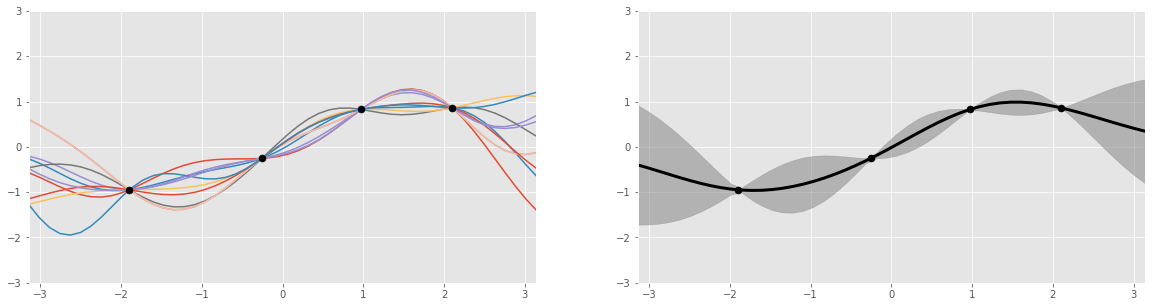
مقاله اسکار نگ اطلاعات خوبی در مورد کارکرد توابع حاصل از فرآیند گاوسی ارائه میدهد.
دلیل اینکه فرآیندهای گاوسی و برخی دیگر از روشهای برازش منحنی برای مدلسازی تابع جایگزین به کار میروند به ذات بیزی آنها برمیگردد. فرآیند گاوسی یک توزیع احتمال است، مانند توزیعی از نتایج یک رویداد (برای مثال احتمال ½ در پرتاب سکه)، با این تفاوت که این توزیع، احتمالات مربوط به همهی توابع ممکن را در برمیگیرد.
برای نمونه، شاید یک مجموعه نقطهداده را به نحوی تعریف کنیم که 40% آنها توسط تابع a(x)، 10% توسط تابع b(x) و به همین ترتیب، قابل بازنمایی باشد. وقتی تابع جایگزین را به صورت یک توزیع احتمال در میآوریم، میتوانیم آن را با اطلاعات جدید و به وسیلهی فرآیندهای احتمال بیزی به روز رسانی کنیم. بدین ترتیب شاید بعد از بروزرسانی بفهمیم تابع a(x) تنها نمایندهی 20% دادههاست. این تغییرات توسط فرمولهای بیزی مدیریت میشوند.
برازش تابع بر اساس نقطهدادههای جدید، با استفاده از روشی همچون رگرسیون چندجملهای Poly-nominal regression کار دشوار یا حتی غیرممکنی خواهد بود.
تابع جایگزین که نقش توزیع احتمال پیشین را دارد، با یک تابع اکتسابی بروزرسانی میشود. این تابع مسئول آزمایش مجموعه نقاط جدید است؛ تابع اکتسابی این کار را طی یک فرآیند اکتشاف و بهرهبرداری انجام میدهد:
- طی بهرهبرداری، از ناحیهای که مدلِ جایگزین، هدف خوبی را پیشبینی میکند نمونهگیری انجام میشود. در این مرحله از نقاط امیدوارکنندهی شناختهشده (نقاطی که احتمال وجود کمینه در آنها بیشتر است) استفاده میشود. با این حال، اگر یک ناحیه و اطلاعاتی که از پیش شناختهشده هستند را به اندازهی کافی جستجو کرده باشیم، به بهرهی چندانی نخواهیم رسید.
- هدف از اکتشاف، نمونهگیری از ناحیهای است که ابهام بالایی دارد. بدین طریق اطمینان حاصل میشود که هیچ ناحیهی بزرگی در فضا بدون جستجو باقی نمانده باشد. کمینهی محلی میتواند در همین نواحی قرار داشته باشد.
اگر یک تابع اکتسابی بار بیشتری به بهرهبرداری بدهد و اکتشاف را کمرنگ در نظر بگیرد، مدل بعد از همان کمینهای که ابتدا پیدا کرده است (که اغلب کمینهی محلی است) کنارهگیری خواهد کرد؛ به عبارتی تنها در همان ناحیهی آشنا باقی میماند. از سوی دیگر، تابع اکتسابی که در مقایسه با بهرهبرداری، به اکتشاف اهمیت بیشتری دهد، اصلاً در کمینه (چه محلی و چه سراسری) باقی نخواهد ماند. بنابراین میتوان گفت دستیابی به نتایج خوب در گروی برقراری توازن بین این دو جنبه است.
تابع اکتسابی که با a(x) نشان میدهیم باید هم بهرهبرداری و هم اکتشاف را مدنظر قرار دهد. از توابع اکتسابی رایج میتوان به بهبود موردانتظار و بیشترین احتمال بهبود اشاره کرد؛ همهی این توابع، احتمال به سود رسیدن یک ورودی خاص را محاسبه میکنند و این کار را بر اساس اطلاعات پیشین انجام میدهند (فرآیند گاوسی).
حال هرآنچه گفتیم را کنار هم قرار میدهیم و به صورت یکپارچه بررسی میکنیم؛ بهینه سازی بیزی به این صورت اجرا میشود:
- تعریف توزیع پیشین مربوط به تابع جایگزین (تابع مبتنی بر فرآیند گاوسی)؛
- انتخاب چندین نقطهداده x به صورتی که تابع اکتسابی a(x) که روی توزیع پیشین کنونی اجرا میشود، به مقدار بیشینه برسد.
- ارزیابی نقطهدادهها x در تابع هزینهی هدف c(x) و تولید نتایج y؛
- بروزرسانی توزیع پیشین فرآیند گاوسی با دادههای جدید به منظور تولید توزیع پسین (که خود در گام بعدی نقش پیشین را خواهد داشت).
- تکرار چندبارهی گامهای 2 تا
- تفسیر توزیع فرآیند گاوسی (که اصلاً هزینهبر نیست) به منظور یافتن کمینهی سراسری.
میتوان گفت بهینه سازی بیزی شامل افزودن احتمالات به بهینهسازی جایگزین است. ترکیب این دو رویکرد سیستمی قدرتمند به دست میدهد که در حوزههای گوناگونی، از ساخت محصولات دارویی گرفته تا خودروهای خودران، کاربرد دارد.
البته در یادگیری ماشین، بهینه سازی بیزی بیشتر در بهینهسازی هایپرپارامترها به کار میرود. برای نمونه، اگر بخواهید یک مدل کلاسبندی ارتقای گرادیان را آموزش دهید، با دهها پارامتر سر و کار خواهید داشت (نرخ یادگیری، عمق بیشینه، حداقل مقدار تجزیه ناخالصی و …). در این صورت، x نمایندهی هایپرپارامترهای مدل و c(x) نمایندهی عملکرد مدل با هایپرپارامترهای x خواهد بود.
دلیل اصلی روی آوردن به بهینه سازی بیزی موقعیتهایی بودند که ارزیابی خروجی در آنها بسیار هزینهبر بود. در این شرایط، ابتدا یک مجموعه درخت تصمیم با چندین پارامتر ساخته شده و سپس در چندین مسئلهی پیشبینی اجرا میشدند؛ این فرآیند هزینهی زیادی دارد.
ارزیابی شبکهی عصبی برای محاسبهی تابع زیان، با استفاده از یک مجموعه پارامتر سرعت بیشتری دارد. زیرا تنها لازم است چندبار ضرب ماتریسی اجرا شود که اگر سختافزار تخصصی داشته باشیم کار بسیار سریعی خواهد بود. یکی از دلایل محبوب ماندن روش گرادیان کاهشی همین امر است.
پس در جمعبندی مطالب میتوان گفت:
- در رویکرد بهینهسازی جایگزین، از طریق نمونهگیری، تابعی جایگزین برای برآورد تابع هدف ایجاد میشود.
- رویکرد بهینه سازی بیزی، روش بهینهسازی جایگزین را وارد چارچوب احتمالات میکند؛ بدین صورت که توابع جایگزین را توزیعهای احتمالی در نظر میگیرد که باید بر اساس اطلاعات جدید بروزرسانی شوند.
- برای ارزیابی احتمال اکتشاف یک نقطهی خاص (در فضایی که با توجه به پیشین میتواند خروجی خوبی تولید کند)، از توابع اکتسابی استفاده میشود؛ توابع اکتسابی بین اکتشاف و بهرهوری توازن برقرار میکنند.
- از بهینه سازی بیزی معمولاً در تنظیم هایپرپارامترها، زمانی که ارزیابی تابع زیان گران و هزینهبر است، استفاده میشود. کتابخانههای زیادی برای این مسئله وجود دارند که از جملهی آنها میتوان به HyperOpt اشاره کرد.





