حل مسائل ریاضی به وسیله هوش مصنوعی
محققان، سیستمی جدید ساختهاند که برای حل مسائل ریاضی دبستان آموزش دیده است. دقت این سیستم، نزدیک به دوبرابر مدل GPT-3 است که به دقت تنظیم شده باشد. این مدل میتواند 90 درصد مسائلی را که دانشآموزان حل کردهاند، پاسخ دهد. در این پروژه، نمونه کوچکی از کودکان 9 تا 12 ساله به یکی از امتحانات ریاضی موجود در دیتاست پاسخ داده و نمره 60 درصد گرفتهاند. سیستم مذکور در همین امتحان عملکرد 55 درصد داشته است. شاید از خود بپرسید اهمیت این دستاورد چیست؟ در پاسخ باید گفت که درحالحاضر، هوش مصنوعی در استدلال چندگامی و عقل سلیم عملکردی ضعیف دارد؛ اینها مسائلی هستند که حتی کودکان دبستانی هم به آسانی از پس آن بر میآیند. این مدل به نحوی آموزش دیده، تا متوجه اشتباههای خودش بشود و روند استدلالی خود را آنقدر تکرار کند، تا بالاخره به راهحل درست دست یابد.
مدلهای زبانی بزرگ
مدلهای زبانی بزرگ همچون GPT-3 مهارتهایی خارقالعاده دارند که از جمله آنها میتوان به قابلیت تقلید سبکهای نوشتاری مختلف و دانش عمومی گستردهشان اشاره کرد. با این حال، این مدلها در حل مسائلی که نیاز به استدلال دقیق چندمرحلهای دارند، همچون حل مسائل ریاضی دبستان، به مشکل بر میخورند. این مدلها میتوانند فرایند راهحلهای درست را تقلید کنند؛ اما در منطق خود مرتکب اشتباههای بحرانی میشوند.
مدلها برای اینکه بتوانند در فرایندهای منطقی پیچیده، عملکردی در سطح انسانها داشته باشند، باید اشتباههای خودشان را تشخیص دهند و قدمهایشان را با دقت انتخاب کنند. اینجاست که مدلهای اعتبارسنج وارد کار میشوند و صحت راهکارهای پیشنهادی را میسنجند. در این پروژه، برای ارزیابی روشها از دیتاست جدید GSM8K استفاده شده است؛ محققان، این دیتاست را در دسترس عموم قرار دادهاند.
در این قسمت، ده مثال از مسائل ریاضی دبستان را مشاهده میکنید که به جز راهحل و نتایج مدل جدید، راهحلهای مدل اعتبارسنج، مدل خط پایه و مدل «به دقت تنظیمشده» را نیز نشان میدهند.
مسئله ریاضی اول |
| علی در یک مدرسه خصوصی مشغول به کار است و یک کلاس تدریس میکند. جان در مدرسهای دولتی کار میکند و دو کلاس دارد. هر کدام از کلاسهای جان، یک هشتم کلاس علی گنجایش دارند. کلاس علی 120 دانشآموز دارد. گنجایش هر دو مدرسه جمعاً چقدر است؟ |
| Method: 175B Verification
Ali’s class has a capacity of 120 students. کلاس علی 120 نفر گنجایش دارد. Each of John’s classes has a capacity of 120/8 = 15 students. هر کدام از کلاسهای جان، یک هشتم کلاس علی گنجایش دارند؛ در نتیجه: 15=8÷120 The total capacity of John’s two classes is 15 students * 2 classes = 30 students. گنجایش دو کلاس جان برابر است با: 30=15×2 The combined capacity of the two schools is 120 students + 30 students = 150 students. گنجایش هر دو مدرسه برابر است با: 150=120+30 |
| Method: 175B Fine-tuning
Each of John’s classes has the capacity of 120 students / 8 = 15 students. گنجایش هر کدام از کلاسهای جان، برابر یک هشتم کلاس علی است؛ بنابراین: 15= 8÷120 So, the two classes that John teaches have a combined capacity of 15 students * 2 = 30 students. دو کلاسی که جان درس میدهد، جمعاً 30=15×2 نفر دانشآموز دارند. Ali’s class has a capacity of 120 students * 1 = 120 students. کلاس علی 120 نفر گنجایش دارد و چون یک کلاس درس میدهد، پس: 120=120×1 Thus, the total capacity of Ali’s school is 120 students + 30 students = 150 students. بنابراین گنجایش کل مدرسه علی برابر است با: 150=120+30 Therefore, the combined capacity of both schools is 150 students + 30 students = 180 students. در آخر، گنجایش هر دو مدرسه با هم برابر است با: 180=150+30 |
| Method: 6B Fine-tuning
Ali has 120 students in one class and there are 8 students in each of his classes so he has 120/8 = 15 classes علی 120 دانشآموز در یک کلاس دارد و در هر کلاسش 8 دانشآموز دارد. پس در کل 15=8÷120 کلاس دارد. The total capacity of all of his classes is 15*120 = 1800 students گنجایش کل کلاسهایش برابر با 1800=120×15 دانشآموز است. John has two classes with 1/8 the capacity of Ali’s class each so he has 2*15 = 30 students in each of his classes جان دو کلاس دارد که ۸/۱ ظرفیت کلاس علی، دانشآموز دارد؛ پس 2 کلاس 15 نفره دارد که جمعاً 30=2×15 دانشآموز دارند. The total capacity of both of John’s classes is 30*2 = 60 students گنجایش کل کلاسهای جان برابر است با: 60=3×20 Combined, the total capacity of both schools is 1800+60 = 1860 students در کل، گنجایش کلاسهای هر دو نفر برابر است با: 1860=60+1800 |
| Method: 6B Verification
If each class has 1/8 of the capacity of Ali’s class, the combined capacity of John’s classes is 1/8*120=15.0 اگر هر کلاس ۸/۱ کلاس علی گنجایش داشته باشد، مجموع ظرفیت کلاسهای جان برابر است با 15= 8/1×120 Combined, the two schools have the capacity of 15.0+120=135.0 در کل، دو مدرسه با هم 135=15+120 نفر دانشآموز دارند. |
مسئله ریاضی دوم |
| تیم 5 درخت میکارد. هر سال 6 لیمو از هر درخت برداشت میکند. بعد از ده سال، تیم چند لیمو از درختهایش میگیرد؟ |
| Method: 175B Verification
He gets 5*6=30 lemons per year تیم 30=5×6 لیمو در هر سال میگیرد He gets 30*10=300 lemons in 10 years تیم در هر 10 سال، 300=10×30 لیمو میگیرد |
| Method: 175B Fine-tuning
He grows 5*12=60 trees تیم 60=5×12 درخت دارد So he gets 60*6=360 lemons a year پس تیم در هر سال 360=60×60 لیمو میگیرد That means he gets 360*10=3600 lemons in a decade تیم در طی ده سال، 3600=10×360 لیمو از درختهایش میگیرد |
| Method: 6B Verification
Tim collects a total of 5*6= 30 lemons per tree. تیم در هر سال، از همه درختهایش 30=5×6 لیمو میچیند So in a decade, he gets 30*10= 300 lemons. پس در ده سال، او 300=10×30 لیمو جمع خواهد کرد |
| Method: 6B Fine-tuning
He gets 5*6=30 lemons a year تیم در هر سال 30=5×6 لیمو میچیند So he gets 30*10=300 lemons in a decade پس در ده سال، او 300=10×30 لیمو جمع خواهد کرد |
مسئله ریاضی سوم |
| آنتونی 50 مداد دارد. او یک دوم مدادهایش را به برندون میدهد و سه پنجم از آنچه برایش باقی مانده، به چارلی میدهد. چند مداد برای آنتونی باقی میماند؟ |
| Method: 175B Verification
Anthony gave 50/2= 25 pencils to Brandon. آنتونی 25=2÷50 مداد به برندون داده است After giving Brandon 25 pencils, Anthony had 50-25= 25 pencils left. بعد از اینکه او 25 مداد به برندون میدهد، 25=25-50 مداد برایش باقی میماند Anthony gave 25*3/5= 15 pencils to Charlie. آنتونی 15=5/3÷25 تا از مدادهایش را به چارلی میدهد After giving Charlie 15 pencils, Anthony had 25-15= 10 pencils left. بعد از اینکه 15 مداد به چارلی میدهد، 10=15-25 مداد برایش باقی میماند Therefore, Anthony kept 10 pencils. پس در آخر، 10 مداد برای آنتونی باقی میماند |
| Method: 175B Fine-tuning
Anthony gave Brandon 50 x 1/2 = 25 pencils. آنتونی 25=2/1÷50 مداد به برندون داده است So he had 50 – 25 = 25 pencils left. پس 25=25-50 مداد برایش باقی میماند Charlie received 25 x 3/5 = 15 pencils. چارلی 15=5/3×25 مداد میگیرد Thus, Anthony kept 25 – 15 = 10 pencils. پس آنتونی 10=15-25 مداد برای خودش نگه میدارد |
| Method: 6B Verification
Anthony gave 1/2 * 50 = 25.0 pencils to Brandon. آنتونی 25=50×2/1 مداد به برندون میدهد There are 50 – 25 = 25 pencils left. 25=25-50 مداد باقی میماند He gave 3/5 * 25 = 15.0 pencils to Charlie. آنتونی 15=25×5/3 مداد به چارلی میدهد Anthony kept 25 – 15 = 10.0 pencils. آنتونی 10=15-25 مداد برای خودش نگه میدارد |
| Method: 6B Fine-tuning
Anthony gave Brandon 50 / 2 = 25.0 pencils. آنتونی 25=2÷50 مداد به برندون میدهد Anthony gave Charlie 50 / 3 = 16.666666666666668 pencils. آنتونی 666666666666668/16=3×50 مداد به چارلی میدهد So, Anthony gave a total of 25 + 16 = 41 pencils to Brandon and Charlie. پس آنتونی در کل 41=16+25 مداد به برندون و چارلی میدهد Therefore, Anthony kept 50 – 41 = 9 pencils. در آخر، 9=41-50 برای آنتونی باقی میماند |
مسئله ریاضی چهارم |
| جان به خانه دوستش میرود که در فاصله 200 مایلی او قرار دارد. او با سرعت 70 مایل در ساعت رانندگی میکند. او مسیر فرعیای را انتخاب میکند که 10 مایل به مسیرش اضافه میکند. او بعد از رسیدن به مقصد، از مسیری 240 مایلی به خانه بر میگردد، اما با سرعت 80 مایل در ساعت رانندگی میکند. سفر او در کل چند ساعت طول کشیده است؟ |
| Method: 175B Verification
The trip took 200+10=210 miles مسافتی که جان طی میکند 210=10+200 مایل است He drove 70 mph for 210 miles so he drove for 210/70=3 hours او مسافت 210 مایلی را با سرعت 70 مایل بر ساعت طی میکند؛ پس 3=70÷210 ساعت در راه است The route home was 240 miles and he drove 80 mph so he was driving for 240/80=3 hours مسیر برگشت 240 مایل است و جان با سرعت 80 مایل بر ساعت حرکت میکند. پس 3=80÷240 ساعت در راه است The total trip took 3+3=6 hours کل سفر او 6=3+3 ساعت طول میکشد |
| Method: 175B Fine-tuning
The trip to his friend’s house was 200+10=210 miles سفر جان به خانه دوستش 210=10+200 مایل است So the total trip was 210+240=450 miles پس کل مسافتی که جان سفر میکند، 450=210+240 مایل است That means it took 450/70=6 hours پس در کل، سفر جان 6=70÷450 ساعت طول میکشد |
| Method: 6B Verification
He drives 200+10=210 miles جان 210=10+200 مایل سفر میکند So his trip took 210/70=3 hours پس سفرش 3=70÷210 ساعت طول میکشد His route home was 240/80=3 hours سفر برگشت جان 3=80÷240 ساعت طول میکشد So his trip took 3+3=6 hours پس در کل، سفر جان 6=3+3 ساعت طول میکشد |
| Method: 6B Fine-tuning
The trip started at 7PM and he arrived at 12AM so it took 200-12=188 hours جان ساعت 7 راه میافتد و 12 نیمهشب به مقصد میرسد. پس زمان سفرش 188=12-200 ساعت است He added 10 miles to the main trip so 10+188 = 198 miles 10 مایل به مسافتش اضافه شده است؛ پس کل سفر 198=188+10 مایل است He traveled 240-198 = 42 miles on the way home او در مسیر برگشت به خانه 42=198-240 مایل رانندگی کرده است He went 80 mph for 240 miles so the trip took 240/80 = 3 hours او 240 مایل مسافت برگشت به خانه را با سرعت 80 مایل بر ساعت حرکت کرده است؛ پس 3=80÷240 ساعت در راه است So in total it took 188+42 = 230 hours پس کل سفر او 230=42+188 ساعت طول میکشد |
مسئله ریاضی پنجم |
| ریچارد، جری و رابرت، 60 گیلاس دارند. اگر رابرت 30 گیلاس داشته باشد و تعداد گیلاسهایش 10 تا از گیلاسهای ریچارد بیشتر باشد، رابرت چند گیلاس بیشتر از جری دارد؟ |
| Method: 175B Verification
Robert has 30 + 10 = 40 cherries. رابرت 40=10+30 گیلاس دارد If there are 60 cherries to be shared, then Richard and Jerry will have 60 – 40 = 20 cherries each. اگر جمعاً 60 گیلاس وجود داشته باشد، ریچارد و جری هر کدام 20=40-60 گیلاس دارند Robert has 40 – 20 = 20 more cherries than Jerry. تعداد گیلاسهای رابرت 20=20-40 تا بیشتر از جری است |
| Method: 175B Fine-tuning
Robert has 30 + 10 = 40 cherries. رابرت 40=10+30 گیلاس دارد Richard has 40 – 10 = 30 cherries. ریچارد 30=10-40 گیلاس دارد Jerry has 30 – 30 = 0 cherries. جری 0=30-30 گیلاس دارد Robert has 40 – 0 = 40 more cherries than Jerry. پس رابرت 40=0-40 گیلاس بیشتر از جری دارد |
| Method: 6B Verification
If Robert has 30 cherries, and has 10 more cherries than Richard, he has 30+10 = 40 cherries. اگر رابرت 30 گیلاس داشته باشد و تعداد گیلاسهایش 10 تا بیشتر از ریچارد باشد، جمعاً 40=10+30 گیلاس دارد Since Jerry has 60 cherries, Robert has 60-40 = 20 more cherries than Jerry. جری 60 گیلاس دارد، پس رابرت 20=40-60 گیلاس بیشتر از جری دارد |
| Method: 6B Fine-tuning
If Robert has 30 cherries, and Richard has 30+10 = 40 cherries, اگر رابرت 30 گیلاس داشته باشد، ریچارد 40=10+30 گیلاس دارد Robert has 40-30 = 10 more cherries than Jerry. رابرت 10=3-40 گیلاس بیشتر از جری دارد |
مسئله ریاضی ششم |
| کاترین میخواهد 5 سبد هدیه درست کند. او میخواهد در هر سبد، 3 گل اطلسی و 2 گل سیبزمینی شیرین بگذارد. گل اطلسیها هر کدام 3 دلار و گلهای سیبزمینی شیرین هر کدام 5/2 دلار هستند. کاترین برای پر کردن 5 سبد چقدر باید هزینه کند؟ |
| Method: 175B Verification
She needs 3 petunias per basket and she has 5 baskets, so she needs 3*5 = 15.00 worth of petunias کاترین برای پر کردن هر سبد به 3 گل اطلسی نیاز دارد و میخواهد 5 سبد را پر کند. پس 15=5×3 دلار قیمت گلهای اطللسی میشود She also needs 2 sweet potato vines per basket and she has 5 baskets, so she needs 2*5 = 10.00 worth of sweet potato vines کاترین در هر سبد 2 گل سیبزمینی شیرین قرار میدهد و چون میخواهد 5 سبد پر کند، 10=5×2 دلار باید برای گلهای سیبزمینی شیرین هزینه کند In total she needs 15.00 worth of petunias and 10.00 worth of sweet potato vines for a total of 15+10 = 25.00 در کل، 15 دلار، هزینه گلهای اطلسی و 10 دلار قیمت گلهای سیبزمینی شیرین میشود؛ پس هزینه کل 25=10+15 دلار است |
| Method: 175B Fine-tuning
She wants 3 petunias in each basket and they cost $3.00 each so that’s 3*3 = $9.00 کاترین در هر سبد 3 گل اطلسی دارد که هر کدام 3 دلار هستند. پس برای قیمت گلهای اطلسی هر سبد 9=3×3 دلار میشود She wants 2 sweet potato vines in each basket and they cost $2.50 each so that’s 2*2.50 = $5.00 او در هر سبد 2 گل سیبزمینی شیرین دارد که هر کدام 5/2 دلار هستند. پس قیمت گلهای سیبزمینی شیرین هر سبد 5=5/2×2 دلار میشود The petunias cost $9.00 and the sweet potato vines cost $5.00 for a total of 9+5 = $14.00 per basket قیمت گلهای اصلی هر سبد 9 دلار و قیمت گلهای دیگر هر سبد 5 دلار هستند. پس برای هزینه درست کردن هر سبد 14=5+9 دلار است She has 5 hanging baskets to fill and they cost $14.00 each so she will spend 5*14 = $70.00 filling all 5 baskets کاترین میخواهد 5 سبد درست کند که هر کدام 14 دلار هستند؛ پس در کل باید 70=14×5 دلار هزینه کند |
| Method: 6B Verification
For the petunias, Katherine will spend 5 petunias x $3.00/petunia = $15.00 کاترین برای گلهای اطلسی 15=3×5 دلار هزینه میکند For the sweet potato vines, she will spend 2 vines x $2.50/vine = $5.00 او برای گلهای سیبزمینی شیری، 5=5/2×2 دلار هزینه میکند Altogether, she will spend $15.00 + $5.00 = $20.00 پس کاترین سرجمع باید 20=5+15 دلار هزینه کند |
| Method: 6B Fine-tuning
She wants to add 3 petunias and 2 sweet potato vines to each basket so that’s 3+2 = 5 plants کاترین در هر سبد 3 گل اطلسی و 2 گل سیبزمینی شیرین قرار میدهد که جمعاً 5=3×2 گل هستند The petunias cost $3.00 each so she will spend 3*5 = $15.00 on petunias قیمت هر گل اطلسی 3 دلار است، پس 15=3×5 دلار برای گلهای اطلسی باید هزینه کند The sweet potato vines cost $2.50 each so she will spend 2.5*5 = $12.50 on sweet potato vines قیمت هر گل سیبزمینی شیرین 5/2 دلار است، پس 5/12=5×5/2 دلار برای این گلها هزینه میکند All total, she will spend 15+12.50 = $27.50 filling all 5 baskets در کل، 50/27=5/12+15 دلار برای هر 5 سبد هزینه پرداخت کند |
مسئله ریاضی هفتم |
| دبرا یک روز را به تماشای یک کندو مینشیند، تا ببیند چند زنبور از آن خارج و به آن وارد میشوند. در 6 ساعت اول، دبرا 30 زنبور را میبیند که از کندو خارج میشوند؛ یک دوم آنها طی 6 ساعت بعدی به کندو بر میگردند. در شش ساعت بعدی، دو برابر تعداد زنبورهایی که اولین بار کندو را ترک کردند، از کندو خارج میشوند و به آن بر میگردند. در شش ساعت آخر، همه زنبورهایی که قبلاً از کندو خارج شده بودند، اما به آن برنگشته بودند نیز به آن بر میگردند. در 6 ساعت آخر، دبرا چند زنبور را دیده که به کندو برگشتهاند؟ |
| Method: 175B Verification
Debra saw 30 bees leave the hive in the first 6 hours and then 1/2 that many bees return in the next 6 hours, 30 / 2 = 15 bees return to the hive in the next 6 hours. دبرا در 6 ساعت اول 30 زنبور را دیده که از کندو خارج شدهاند و 2/1 آنها در 6 ساعت بعدی برگشتهاند. پس 15=2÷30 زنبور به کندو برگشتهاند. She saw 30 bees leave the hive and then 15 bees return to the hive, 30 – 15 = 15 bees still haven’t returned to the hive. او دیده است 30 زنبور کندو را ترک کرده و 15 تا به آن برگشتهاند، پس 15=15-30 زنبور هنوز به کندو برنگشتهاند Two times as many bees as she saw first leave the hive fly from the hive and leave in the next 6 hours, 2 * 30 = 60 bees leave the hive in the next 6 hours. در شش ساعت بعدی، دو برابر آنچه دفعه اول دیده بود از کندو خارج میشوند. پس 60=30×2 زنبور در این بازه زمانی از کندو خارج شدهاند In total she saw 30 bees leave the hive and 15 bees return, 30 + 15 = 45 bees. در کل، 30 زنبور کندو را ترک کرده و 15 زنبور به آن برگشتهاند؛ پس 45=15+30. After the bees that hadn’t already returned did so, there were still 15 bees missing from the hive, so the total number of bees Debra saw return to the hive is 45 + 15 = 60 bees. بعد از اینکه آن تعداد زنبوری که به کندو برنگشته بودند نیز به آن برگشتند، 15 زنبور همچنان بیرون از کندو باقی میمانند. پس در کل، تعداد زنبورهایی که دبرا در حال بازگشت به کندو دیده برابر است با 60=15+40 |
| Method: 175B Fine-tuning
Debra sees 30 bees leave the hive in the first 6 hours. دبرا در 6 ساعت اول 30 زنبور را دیده که از کندو خارج میشوند She sees 1/2 * 30 bees = 15 bees return to the hive in the next 6 hours. او 15=2/1÷30 زنبور را میبیند که در شش ساعت بعدی به کندو بر میگردند She sees 2 * 15 bees = 30 bees fly from the hive and leave in the next 6 hours. در شش ساعت بعدی، دبرا 30=15×2 زنبور را میبیند که از کندو خارج میشوند Before the last 6 hours, Debra saw 30 + 15 + 30 = 75 bees leave the hive. قبل از 6 ساعت آخر، 75=30+15+30 زنبور از کندو خارج شدهاند Before the last 6 hours, Debra saw 75 – 30 = 45 bees return to the hive. قبل از شش ساعت آخر، دبرا 45=30-75 زنبور به کندو بر میگردند |
| Method: 6B Verification
First find the total number of bees that left the hive: 30 bees * 6 hours = 180 bees اول تعداد کل زنبورهایی را که از کندو خارج شدهاند، حساب میکنیم که میشود 180=6×30 Then subtract the number of bees that left in the first 6 hours from the number that returned: 180 bees – 30 bees = 150 bees سپس تعداد زنبورهایی را که در 6 ساعت اول به کندو برگشتهاند، از تعداد زنبورهایی که از آن خارج شدهاند کم میکنیم: 150=30-180 Then multiply that number by two to find the number of bees that returned: 150 bees * 2 = 300 bees سپس تعداد را در دو ضرب میکنیم، تا تعداد زنبورهایی را که برگشتهاند، پیدا کنیم: 300=2×150 |
| Method: 6B Fine-tuning
Debra saw 30 bees leave the hive in the first 6 hours, 1/2 that number in the next 6 hours, and then 2*that number in the next 6 hours. دبرا در شش ساعت اول، 30 زنبور را در حال ترک کندو دیده است که در شش ساعت بعدی 2/1 و در شش ساعت سوم، 2 برابر آن را میبیند The total number of bees that left the hive in the last 6 hours is 30+1/2 that number+2*that number = 33.0 تعداد کل زنبورهایی که در 6 ساعت آخر کندو را ترک کردهاند، 33=(2)30+(2/1)30+30 است She saw two times as many bees as she saw first leave the hive fly from the hive and leave in the next 6 hours, 33*2 = 66 bees دو برابر این تعداد کندو را ترک کرده و در 6 ساعت بعدی به آن بر میگردند، پس: 66=2×33 The total number of bees that left the hive and returned in the next 6 hours is 66+33 = 99 bees تعداد کل زنبورهایی که کندو را ترک کرده و در شش ساعت بعدی به آن برگشتهاند، برابر است با 99=33+66 |
مسئله ریاضی هشتم |
| حجم کمد تیموتی 24 اینچ مکعب است. اندازه کمد زک نصف اندازه کمد تیموتی است و کمد پیتر یک چهارم اندازه کمد زک است. کمد پیتر چند اینچ مکعب است؟ |
| Method: 175B Verification
If Zack’s locker is half the size of Timothy’s locker, then it is 24 / 2 = 12 cubic inches. اگر کمد زک نصف کمد تیموتی باشد، اندازهاش 12=2÷24 اینچ مکعب خواهد بود If Peter’s locker is 1/4 the size of Zack’s locker, then it is 12 / 4 = 3 cubic inches. اگر کمد پیتر 4/1 اندازه کمد زک باشد، 3=4÷12 اینچ مکعب خواهد بود |
| Method: 175B Fine-tuning
Zack’s locker is 24/2=12 cubic inches. کمد زک 12=2÷24 اینچ مکعب است Peter’s locker is 12/4=3 cubic inches. اندازه کمد پیتر 3=4÷12 اینچ مکعب است |
| Method: 6B Verification
Zack’s locker is 24/2 = 12.0 cubic inches. کمد زک 12=2×24 اینچ مکعب است Peter’s is 12/4 = 3.0 cubic inches. اندازه کمد پیتر 3=4÷12 اینچ مکعب است |
| Method: 6B Fine-tuning
Zack’s locker is 24/2 = 12 cubic inches. اندزه کمد زک 12=2÷24 اینچ مکعب است Peter’s locker is 12/4 = 3 cubic inches. اندازه کمد پیتر 3=4÷12 اینچ مکعب است |
مسئله ریاضی نهم |
| آملیا، مگان و دیور، کارهای خانه را تقسیم کردند، به نحوی که هر موقع دو نفر سر کار بودند، نفر سوم مشغول انجام این کارها باشد. کار آملیا زدن چمنها بود که 4 ساعت طول میکشید. مگان مسئول بیرون بردن سگ بود که 2 ساعت بیشتر از کار آملیا طول میکشید. کار دیور هم شستن لباسها بود که 4 ساعت بیشتر از کار آملیا طول میکشید. کل زمانی را که هر سه نفر به انجام کارهای خانه اختصاص دادهاند، محاسبه کنید. |
| Method: 175B Verification
Amalia’s chore was to mow the lawn, which took her 4 hours. کار آملیا، زدن چمنهای باغچه بوده است که 4 ساعت طول کشیده است Megan’s chore was to walk the dog, which took 2 hours longer than Amalia’s work, so she took 4+2 = 6 hours to do her chore. کار مگان بیرون بردن سگ بوده که 2 ساعت بیشتر از کار آملیا طول میکشد، یعنی 6=4+2 ساعت Dior’s chore was to do laundry, which took 6 hours longer than Amalia’s work, so 6+4 = 10 hours for her to complete her chore. کار دیور شستن لباسها بوده است که 6 ساعت بیشتر از کار آملیا طول میکشد، یعنی 10=4+6 ساعت The total time they all took doing their chores is 4+6+10 = 20 hours کل زمانی که این سه نفر صرف انجام کارهایشان کردهاند برابر است با 20=10+6+4 ساعت |
| Method: 175B Fine-tuning
Amalia took 4 hours to mow the lawn. آملیا 4 ساعت صرف زدن چمنها میکند Megan took 2 hours longer to walk the dog than Amalia, so 4 + 2 = 6 hours. مگان ۲ ساعت بیشتر از کار آملیا صرف بیرون بردن سگ میکند، یعنی 6=2+4 ساعت Dior took well over 4 hours to do the laundry, meaning she took 4 + 6 = 10 hours. دیور 4 ساعت بیشتر از این برای شستن لباسها صرف میکند، یعنی 10=6+4 ساعت Altogether, they took 4 + 6 + 10 = 20 hours to do their chores. پس این سه نفر در مجموع 20=10+6+4 ساعت صرف کارهایشان کردهاند |
| Method: 6B Verification
If Megan’s chore took 2 hours longer than Amalia’s, then it took 4+2 = 6 hours to complete. اگر کار مگان 2 ساعت بیشتر از کار آملیا طول کشیده باشد، یعنی 6=2+4 ساعت صرف کارش کرده است If Dior’s chore took 4 hours longer than Amalia’s, then it took 6+4 = 10 hours to complete. اگر کار دیور 4 ساعت بیشتر از کار آملیا طول کشیده باشد، یعنی 10=6+4 ساعت زمان برده است If you add the time they all took to complete their chores, then you get 4+6+10 = 20 hours. اگر تمام این ساعتها را با هم جمع کنیم، 20=10+4+6 ساعت میشود |
| Method: 6B Fine-tuning
If you add the time Amalia took to mow the lawn, it becomes 4+2 = 6 hours. اگر کار آملیا را جمع کنیم، 6=2+4 ساعت میشود If Megan’s work on the dog took 2 hours longer than Amalia’s, the total time it took to walk the dog was 6+2 = 8 hours. اگر کار مگان را که ۲ ساعت بیشتر از کار آملیا طول میکشد، حساب کنیم، کل زمانی که باید صرف بیرون بردن سگ شود 8=6+2 ساعت است If Dior’s work on laundry took well over 4 hours longer than Amalia’s, the total time it took to do laundry was 4+2 = 6 hours. اگر کار دیور 4 ساعت بیشتر از کار آملیا طول بکشد، شستن لباسها 6=4+2 ساعت زمان میبرد Together, the three took 6+8+6 = 20 hours doing chores. پس در کل، انجام تمامی کارهای خانه 20=6+8+6 ساعت طول میکشد |
مسئله ریاضی دهم |
| جان در هر نیم ساعت یک بطری آب مینوشد. حل هر جدول سودوکوی معمولی 45 دقیقه از او زمان میبرد. حل جدول سودوکوی سخت 4 برابر این مقدار به زمان نیاز دارد. جان در این زمان، چند بطری آب مینوشد؟ |
| Method: 175B Verification
He drinks 1/2 hour so 60 minutes / 2 = 30 minutes جان در هر نیم ساعت، یک بطری آب مینوشد و هر یک ساعت، دو تا سی دقیقه دارد A normal puzzle takes 45 minutes so an Extreme puzzle takes 45*4 = 180 minutes حل یک جدول معمولی 45 دقیقه زمان میبرد، پس حل جدول سودوکوی سخت به 180=4×45 دقیقه زمان نیاز دارد That means he drinks 180/30 = 6 bottles of water پس جان در این زمان 6=30÷180 بطری آب مینوشد |
| Method: 175B Fine-tuning
A normal sudoku puzzle takes 45 minutes to solve so an extreme sudoku takes 4*45 = 180 minutes حل یک جدول سودوکوی ساده 45 دقیقه زمان میبرد، پس برای حل یک جدول ساخت به 180=4×45 دقیقه زمان نیاز است He drinks a bottle of water every half hour and an extreme sudoku takes 180 minutes so he drinks 180/2 = 90 bottles of water جان هر نیم ساعت یک بطری آب مینوشد و از آن جایی که حل یک جدول سودوکوی سخت 180 دقیقه زمان میبرد، 90=2×180 بطری آب در این مدت لازم است |
| Method: 6B Verification
He drinks a bottle every 45 minutes so that’s 1/2*45=22.5 minutes جان هر 45 دقیقه یک بطری آب مینوشد، پس یعنی 5/22=2/1÷45 دقیقه An extreme sudoku takes 4*45=180 minutes یک جدول سودوکوی سخت به 180=4×45 دقیقه زمان نیاز دارد So he drinks 180/22.5=8 bottles of water پس جان 8=5/22÷180 بطری آب نیاز دارد |
| Method: 6B Fine-tuning
He drinks 1.5 bottles of water per hour because 45 / 60 = 0.75 جان در هر یک ساعت 5/1 بطری آب مینوشد، چون 75/0=60÷45 That means he drinks 3 bottles of water because 0.75 x 2 = 1.5 پس میتوان گفت 3 بطری آب نیاز دارد، چون 5/1=2×75/0 |
دیتاست GSM8K
در دیتاست GSM8K، 8500 مسئله ریاضی دبستان وجود دارد. راهحل هر کدام از آنها بین 2 تا 8 گام نیاز دارد. راهحلها شامل مجموعهای از محاسبات متوالی ساده هستند که با استفاده از عملیاتهای پایه (+ – × ÷) اجرا میشوند. نوآورانهترین مدلهای زبانی که به دقت تنظیم شده باشند نیز عملکرد چندان خوبی روی این دیتاست از خود نشان نمیدهند؛ دلیل این امر میتواند گوناگونی بالای مسائل باشد. با این حال، راهحلهای GSM8K مبتنی بر مفاهیم ابتدایی هستند و به همین دلیل، نتایج امیدوارکنندهای از خود نشان میدهند.
راهحلهای GSM8K به جای اینکه ساختار عبارات ریاضی را داشته باشند، به صورت زبان طبیعی نوشته شدهاند. از آنجایی که این راهحلها وابسته به زبان طبیعی هستند، تفسیرشان برای انسانها راحتتر است.
اعتبارسنجها، مدلهایی که از اشتباههای خود درس میگیرند
یکی از چالشهای اساسی استدلال مربوط به ریاضی، حساسیت بالای تکتک اشتباهها است. مدلهای اتورگرسیو (خودرگرسیونی) که راهحلها را توکن به توکن تولید میکنند، هیچ مکانیزمی برای تصحیح اشتباههایشان ندارند. به عبارت دیگر، همانطور که در مثالهای بالا مشاهده کردید، بخشهایی از راهحل که درست نیستند، به سرعت پنهان میشوند و دیگر قابلتشخیص نیستند.
در این پروژه، محققان اعتبارسنجهایی را آموزش دادند، تا میزان درستی راهحلهای مدل را ارزیابی کنند. این اعتبارسنجها راهحلهایی را که به دست خود مدل نوشته شدهاند، دریافت میکنند و سپس آموزش میبینند، تا درستی آنها را تشخیص دهند.
پژوهشگران برای حل هر مسئله جدید آزمایشی، 100 راهحل داوطلب تولید کردند و سپس از طریق اعتبارسنج، مناسبترین راهحل (با بالاترین نمره) را انتخاب کردند. قابلیتی که به کمک اعتبارسنجها میآید، ماهیت اختیاری آنهاست. به علاوه، اعتبارسنجی راهحلها معمولاً آسانتر از تولید آنهاست.
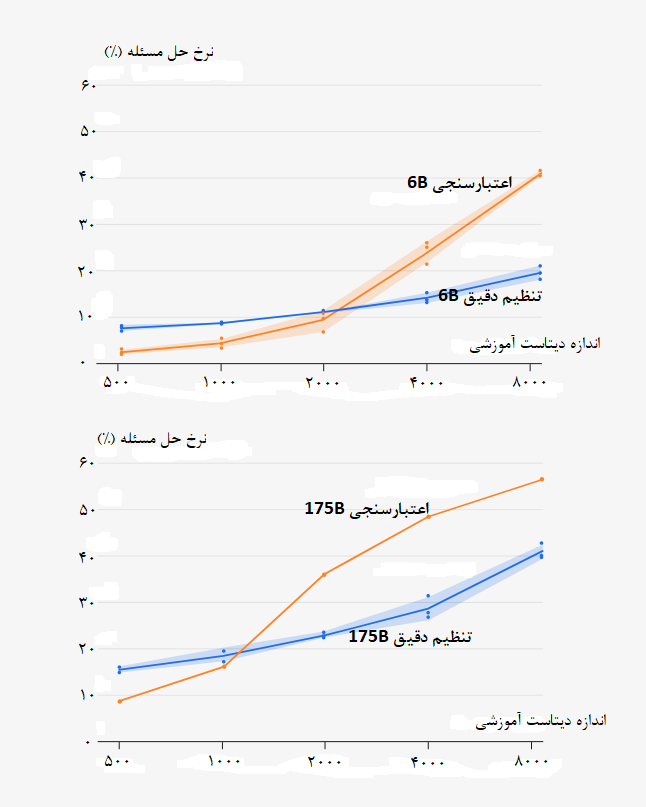
یافتهها نشان دادند که استفاده از مدل اعتبارسنج، عملکرد مدل را بهشدت ارتقا میدهد؛ البته تا زمانی که دیتاست به اندازه کافی بزرگ و جامع باشد. در کار با دیتاستهای کوچک، مدلهای اعتبارسنج دچار مشکل بیشبرازش میشوند، چون به جای یادگیری خواص اصلی استدلال ریاضی، صرفاً پاسخهای نهایی دیتاست آموزشی را حفظ میکنند.
وقتی از کل دیتاست آموزشی استفاده میشود، مدل اعتبارسنج پارامتر 6B عملکرد نسبتاً بهتری از مدل پارامتر 175B (که به دقت تنظیم شده) از خود نشان میدهد. این تفاوت، تقریباً برابر با ارتقای عملکردی است که در صورت افزایش 30 برابری اندازه مدل به دست میآید. علاوه بر این، به نظر میرسد با بسط دادهها، مدل اعتبارسنج به نتایج بهتری هم دست یابد.
جمعبندی
ارائه استدلالهای درست و تشخیص اشتباهها از جمله چالشهای کلیدی هستند که توسعه هوش مصنوعی عمومی را با مانع روبهرو میکنند. مسائل ریاضی دبستان بستر ایدهآلی برای به آزمایش گذاشتن این قابلیتها به شمار میروند. مشکلات GSM8K از نظر مفهومی ساده هستند؛ اما در این نوع مسائل، یک اشتباه کوچک کافی است، تا کل راهحل از مسیر درست خارج شود. تشخیص و اجتناب از اشتباههایی از این دست، مهارتی حیاتی برای مدلها به شمار میرود. با آموزش اعتبارسنجها میتوان به مدلها آموخت، تا بین راهحلهای خوب و راهحلهایی که به جواب نمیرسند، تمیز قائل شوند. به نظر میرسد با پیادهسازی مدلها در حوزههایی که از نظر منطقی پیچیدهتر هستند، میتوان این مهارتها را توسعه بخشید.
انواع کاربردهای هوش مصنوعی در صنایع مختلف را در هوشیو بخوانید