مدیریت دیتاست‌های نامتوزان در مسائل رده‌بندی دودویی (بخش دوم)

در قسمت اول (لینک آن در ادامه مطلب قرار دارد) از این مجموعه، مشکل عدم توازن کلاسی در مسائل رده‌بندی دودویی Binary classification را توضیح دادیم و برخی از راهکارهایی را نیز که برای حل آن وجود دارد، بررسی کردیم؛ آن روش‌ها با مداخله‌ مستقیم بر روی خود دیتاست و به کمک تکنیک‌های نمونه‌برداری گوناگون، توازن داده‌ها را افزایش می‌دادند.

در این قسمت، مجموعه‌ای از تکنیک‌ها را بررسی خواهیم کرد که مستقیماً بر روی فرایند آموزشی اجرا می‌شوند (نه دیتاست). این تکنیک‌ها عبارت‌اند از:

• جایگزین کردن نقطه‌برش‌ها Alternative cutoffs
  
• اختصاص وزن‌های مختلف به نمونه‌ها Weighting instances with different values
  
• نامتقارن کردن تابع زیان Asymmetric loss function
  

در این قسمت، مورد اول یعنی جایگزین کردن نقطه‌برش‌ها را بررسی می‌کنیم. بدین منظور از همان دیتاستی که در مقاله‌ قبلی مثال زدیم، استفاده می‌کنیم (با کمی تغییر). عدم‌توازن این دیتاست را در تصویر پایین مشاهده می‌کنید:

پیش  از این در خصوص رگرسیون لوجیستیک و ROC (منحنی مشخصه عملکرد Receiver operating characteristic) صحبت کردیم و نشان دادیم آستانه‌ کلسیفایر چطور می‌تواند بر نرخ مثبت‌های واقعی و منفی‌های واقعی تأثیر بگذارد.

همان‌طور که در مقاله‌ قبلی توضیح دادیم، از این تکنیک می‌توانیم در موقعیت‌هایی استفاده کنیم که در آن‌ها برخی از معیارها از بقیه مهم‌تر هستند (برای مثال، خطر اینکه یک فرد سالم در کلاس بیماران قرار گیرد، کمتر از این است که یک فرد بیمار در کلاس افراد سالم قرار گیرد).

این تکنیک در مدیریت دیتاست‌های نامتوازن نیز کاربرد دارد. برای درک بهتر به این مثال توجه کنید:

1000 نمونه داریم که 900 مورد از آن‌ها مربوط به کلاس 1 (کلاس مثبت) و تنها 100 مورد متعلق به کلاس 0 (منفی) هستند. الگوریتم ما که فرض می‌کنیم رگرسیون لوجیستیک است، همه‌ این نمونه‌ها را در کلاس 1 قرار می‌دهد و با وجود این، به میزان دقت 90 درصد دست می‌یابد. ماتریس درهم‌ریختگی Confusion matrix چنین شکلی خواهد داشت:

همان‌طور که مشاهده می‌کنید، نرخ منفی‌های کاذب و منفی‌های حقیقی 0 درصد و نرخ مثبت‌های کاذب 10 درصد است. در چنین شرایطی می‌توانیم نقطه‌برش را به نحوی تغییر دهیم که نرخ مثبت‌های کاذب به حداقل برسد. البته این کار به قیمت کاهش نرخ مثبت‌های حقیقی تمام خواهد شد؛ با وجود این، واضح است که برای دستیابی به الگوریتمی قابل‌تعمیم‌تر که به سمت کلاس اکثریت سوگیری نداشته باشد و نمونه‌های منفی را (که نادر اما مهم هستند) نادیده نگیرد، این بهای ناچیزی است.

اینجا پیاده‌سازی این فرایند در پایتون را با استفاده از دیتاست مصنوعی تولیدشده مشاهده می‌کنید:

from sklearn.datasets import make_classification
import pandas as pdX, y_tmp = make_classification(
    n_classes=2, class_sep=1, weights=[0.98, 0.02],
    n_informative=10, n_redundant=0,n_repeated=0, 
    n_features=10,  
    n_samples=10000, random_state=123
)#little trick for terminlogy purpose (positive class = 1, negative class = 0)y = y_tmp.copy()
for i in range(len(y_tmp)):
  if y_tmp[i]==0:
    y[i] = 1
  else:
    y[i] = 0df = pd.DataFrame(X)
df['target'] = y
df.target.value_counts().plot(kind='bar', title='Count (target)', color = ['b', 'g'])

حال، الگوریتم رگرسیون لوجیستیک را آموزش می‌دهیم (بعد از تقسیم دیتاست به دو مجموعه‌ آموزشی و آزمایشی):

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(
       X, y, test_size=0.33, random_state=42)from sklearn.linear_model import LogisticRegression
from sklearn.metrics import classification_report, confusion_matrixmodel = LogisticRegression(random_state=0).fit(X_train,y_train)

اکنون می‌خواهیم نتیجه‌ پیش‌بینی مدل بر روی مجموعه‌ آزمایشی را ببینیم:

نکته: تابع predict()  به صورت پیش‌فرض، مقدار 5/0 را به عنوان نقطه‌برش در نظر می‌گیرد. برای تغییر این نقطه‌برش باید یک تابع پیش‌بینی سفارشی تعریف کنیم که مستقیماً بر اساس احتمالات پیش‌بینی‌شده عمل می‌کند (که از طریق predict_proba() قابل‌بازیابی است).

import matplotlib.pyplot as pltcm = confusion_matrix(y_test, model.predict(X_test))fig, ax = plt.subplots(figsize=(8, 8))
ax.imshow(cm)
ax.grid(False)
ax.xaxis.set(ticks=(0, 1), ticklabels=('Predicted 0s', 'Predicted 1s'))
ax.yaxis.set(ticks=(0, 1), ticklabels=('Actual 0s', 'Actual 1s'))
ax.set_ylim(1.5, -0.5)
for i in range(2):
    for j in range(2):
        ax.text(j, i, cm[i, j], ha='center', va='center', color='red')
plt.show()

همان‌طور که مشاهده می‌کنید، الگوریتم توانسته است از 84 نمونه‌ منفی (کلاس 0) تنها 4 نمونه را به درستی رده‌بندی کند و 80 نمونه‌ دیگر در کلاس مثبت قرار گرفته‌اند. بااین‌حال، دقت کلی همچنان 98 درصد است! مشکل اینجاست که مجموعه‌ آزمایشی نیز مثل دیتاست اصلی نامتوازن است، اما معلوم نیست داده‌های آینده هم این‌طور باشند. بنابراین، به الگوریتمی نیاز داریم که قابلیت تعمیم بر روی داده‌های جدید را نیز داشته باشد.

بدین منظور، نقطه‌برش را تغییر می‌دهیم. وقتی نقطه‌برش 5/0 باشد، هر احتمالی که بالاتر از 5/0 باشد در کلاس 1 (مثبت) قرار می‌گیرد. پس با افزایش نقطه‌برش، رده‌بندی نمونه‌ها در کلاس 1 را دشوارتر می‌کنیم. برای درک بهتر به نمودار ROC (این‌بار برای کل دیتاست) نگاه کنید:

import plotly.express as px
from sklearn.metrics import roc_curve, aucmodel.fit(X, y)
y_score = model.predict_proba(X)[:, 1]fpr, tpr, thresholds = roc_curve(y, y_score)fig = px.scatter(
    x=fpr, y=tpr, color = thresholds,
    title=f'ROC Curve (AUC={auc(fpr, tpr):.4f})',
    labels=dict(x='False Positive Rate', y='True Positive Rate', color = 'Threshold'))fig.add_shape(
    type='line', line=dict(dash='dash'),
    x0=0, x1=1, y0=0, y1=1
)fig.update_yaxes(scaleanchor="x", scaleratio=1)
fig.update_xaxes(constrain='domain')
fig.show()

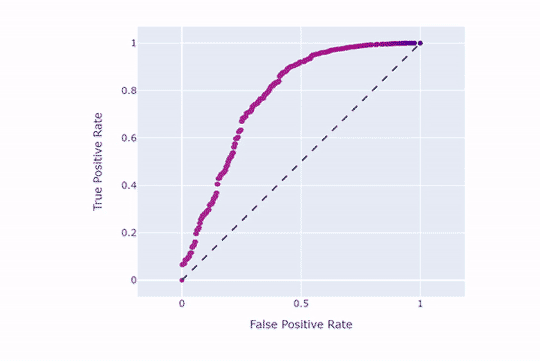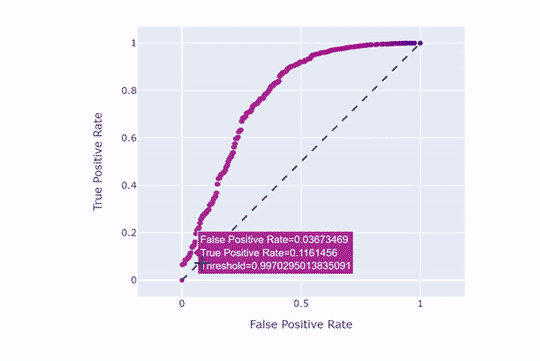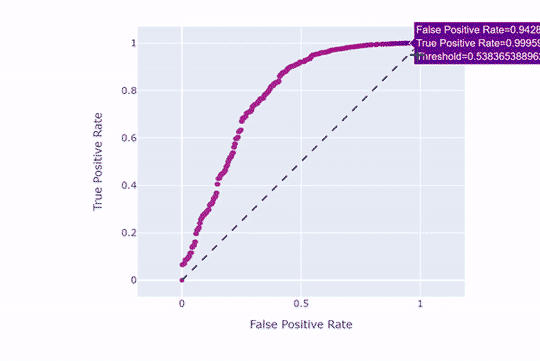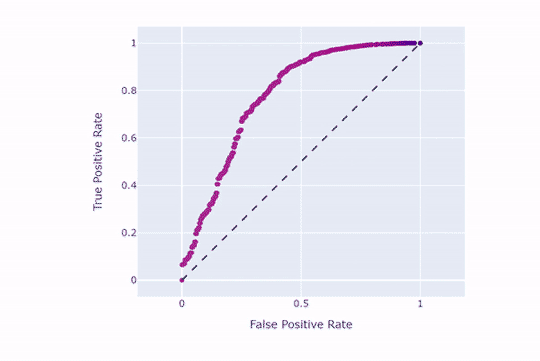
همان‌طور که مشاهده می‌کنید، هر چه نقطه‌برش بالاتر باشد، نرخ مثبت‌های حقیقی و کاذب کاهش می‌یابند. حال همین کار را با نقطه‌برش 9/0 امتحان می‌کنیم:

import numpy as np
thres = 0.9preds = model.predict_proba(X_test)
y_pred = np.where(preds[:,1]>thres,1,0)cm = confusion_matrix(y_test, y_pred)fig, ax = plt.subplots(figsize=(8, 8))
ax.imshow(cm)
ax.grid(False)
ax.xaxis.set(ticks=(0, 1), ticklabels=('Predicted 0s', 'Predicted 1s'))
ax.yaxis.set(ticks=(0, 1), ticklabels=('Actual 0s', 'Actual 1s'))
ax.set_ylim(1.5, -0.5)
for i in range(2):
    for j in range(2):
        ax.text(j, i, cm[i, j], ha='center', va='center', color='red')
plt.show()

از تصویر بالا می‌توان دریافت که الگوریتم توانسته است 24 نمونه‌ را در کلاس منفی رده‌بندی کند.

بسته به معیار عینی و موقعیت‌های دنیای واقعی، می‌توان از نقطه‌برش‌های مختلف استفاده کرد.

جمع‌بندی

در این مقاله مشاهده کردیم، چطور می‌توان یک دیتاست نامتوازن را بدون تغییر دیتاست ورودی و با مداخله‌ مستقیم بر روی کلسیفایر، مدیریت کرد. در قسمت سوم این مجموعه با یک روش دیگر برای مدیریت دیتاست‌های نامتوازن آشنا خواهیم شد.

از طریق لینک زیر می‌توانید به بخش اول دسترسی داشته باشید:

مدیریت دیتاست‌های نامتوازن در مسائل رده‌بندی دودویی (بخش اول)