رگرسیون خطی در پایتون

زمان مطالعه: 5 دقیقه

مقدمات یادگیری ماشینی: قسمت اول

در این نوشتار، قصد داریم ابتدایی‌ترین مدل یادگیری ماشینی یعنی رگرسیون خطی را بسازیم و آن را تنها با استفاده از کتابخانه‌ Numpy پایتون اجرا کنیم. بدین منظور، ابتدا نگاهی به دیتاست خواهیم انداخت، سپس در خصوص فرایند الگوریتم عمومی یادگیری نظارت‌شده صحبت خواهیم کرد و بعد از آن به بازنمایی فرضیه‌ها، توابع زیان و الگوریتم گرادیان کاهشی می‌پردازیم.

در آخر نیز کلاس LinReg را تعریف و آن را روی داده‌ها آزمایش می‌کنیم.

مطالب مجموعه‌ «مقدمات یادگیری ماشینی» بدین قرار خواهند بود:

• رگرسیون خطی در پایتون
• رگرسیون خطی با وزن محلی[6] (وزنی محلی) در پایتون
• معادلات نرمال[7] با استفاده از پایتون: یک راهکار closed-form برای رگرسیون خطی
• رگرسیون چندجمله‌ای[8] در پایتون

رگرسیون خطی

فرض کنید یک دیتاست متشکل از X (ویژگی) و Y (برچسب) داریم و می‌خواهیم یک خط راست را روی آن برازش دهیم. برای مثال از داده‌های پایین استفاده می‌کنیم:

فرض کنید دانشجوی رشته‌ فیزیک هستید و می‌خواهید نمره‌ امتحانتان (از 100) را به ازای ساعات مطالعه محاسبه کنید.

# Imoprting required libraries.
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd# Reading the csv file.
df = pd.read_csv('data.csv')# Displayinng the first five elements of the dataframe.
df.head(10)

در این دیتاست، ساعات مطالعه متغیر X (ویژگی) هستند. در این مسئله فقط یک ویژگی داریم، اما می‌توان ویژگی‌های بیشتری نیز در نظر گرفت (برای مثال، مقدار تمرینی که برای امتحان انجام داده‌اید). نمرات امتحان به‌عنوان Y (برچسب یا هدف) نشان داده می‌شوند. نتیجه‌ مصورسازی داده‌ها

# Taking the Hours and Scores column of the dataframe as X and y 
# respectively and coverting them to numpy arrays.
X = np.array(df['Hours']).reshape(-1,1)
y = np.array(df['Scores'])# Plotting the data X(Hours) on x-axis and y(Scores) on y-axis
plt.figure(figsize=(8,6)) # figure size
plt.scatter(X, y)
plt.title('Hours vs Scores')
plt.xlabel('X (Input) : Hours')
plt.ylabel('y (Target) : Scores')

بدین شکل خواهد بود:

در رگرسیون خطی، هدف برازش یک خط صاف روی دیتاستی همچون دیتاست بالاست؛ در نتیجه‌ آموزش چنین مدلی می‌توان، برای مثال، نمرات را بر اساس ساعات مطالعه پیش‌بینی کرد.

فرایند استاندارد یک الگوریتم یادگیری نظارت‌شده

ابتدا دیتاستی شبیه به جدول 1 داریم. این مجموعه‌داده‌های آموزشی را به الگوریتم یادگیری تغذیه می‌کنیم. خروجی الگوریتم یادگیری تابع h(x) یا تابع فرضیه است که برای پیش‌بینی y (نمره) بر اساس ورودی x (ساعات مطالعه) استفاده می‌شود.

تابع h(x) را چطور نشان می‌دهیم؟

از آنجایی که یک خط صاف می‌خواهیم، فرضیه باید از این معادله پیروی کند:

h(x) = wX + b

w وزن و b سوگیری را نشان می‌دهد.

در کدنویسی، h(x) با y_hat نشان داده می‌شود:

در این مثال، می‌توانیم داده‌ها را در دو بُعد نمایش دهیم، پس می‌توانیم بگوییم weights (وزن) شیب خط و bias (سوگیری) عرض از مبدأ y است؛ اما اگر در داده‌های خود دو ویژگی داشتیم، داده‌ها را در سه بُعد نمایش می‌دادیم؛ در این صورت، برای برازش داده‌ها در فضای سه‌بعدی به یک صفحه نیاز داشتیم. یعنی فرضیه‌ ما به جای یک خط صاف، یک صفحه می‌بود. با افزایش تعداد ویژگی‌ها، ابعاد weights و bias نیز افزایش می‌یابد.

weights و bias بردار هستند و ابعاد w و b برابر با تعداد ویژگی‌هاست.

به weights و bias پارامترهای الگوریتم یادگیری نیز گفته می‌شود.

هدف ما پیدا کردن مقادیری برای weights و bias است، به شکلی که h(x) تا حد امکان به y نزدیک باشد.

معرفی نمادها

n: تعداد ویژگی‌ها (در این مثال فقط یک ویژگی، یعنی ساعات مطالعه داشتیم)

m: تعداد نمونه‌های آموزشی (اینجا 25 عدد بودند)

x: ویژگی‌ها

y: برچسب‌ها/ اهداف

(X(i), y(i)): نمونه‌ iم در مجموعه‌ آموزشی

معرفی x، y، w و b

X ماتریسی به ابعاد (m,n) است. ردیف‌های این ماتریس، نشان‌دهنده‌ نمونه‌های آموزشی و ستون‌های آن نشان‌دهنده‌ ویژگی‌ها هستند.

y ماتریسی به ابعاد (m,1) است. هر کدام از ردیف‌های این ماتریس، برچسب مربوط به ویژگی‌های موجود در ماتریس x هستند.

w برداری به اندازه‌ (n,1) است و پارامتر b مقیاس‌بندی است که می‌تواند انتشار همگانی یابد. برای کسب اطلاعات بیشتر در خصوص انتشار همگانی در NumPy به این لینک مراجعه کنید.

اگر 3 ویژگی و 3 نمونه‌ آزمایشی داشته باشیم (m=3, n=3)، ماتریس‌ها را می‌توان بدین شکل نمایش داد:

اندیس پایین اعداد نشان‌دهنده‌ رتبه‌ نمونه‌ آموزشی (برای مثال، iمین نمونه) و اندیس بالای آن‌ها نشان‌دهنده‌ رتبه‌ ویژگی (برای مثال، iمین ویژگی) است.

پارامترهای w و b را چطور باید انتخاب کرد؟

W و b باید به‌نحوی انتخاب شوند که h(x) تا حد امکان به y نزدیک باشد. پس می‌خواهیم پارامترها را (حداقل برای تعداد ساعات مطالعه‌ای که نمره‌ نتیجه‌ آن‌ها مشخص است) طوری انتخاب کنیم که نمرات تولیدشده از طریق الگوریتم به دیتاست آموزشی (آنچه از پیش می‌دانیم) نزدیک باشد.

تابع زیان

تابع زیان خطای میانگین مجذورات را بدین صورت تعریف می‌کنیم:

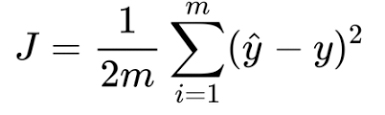
حال باید مقادیر w و b را داشته باشیم، تا بتوانیم تابع زیان را به حداقل برسانیم. H(x) یا yمقدار پیش‌بینی‌شده از طریق الگوریتم و y هم مقدار واقعی است. تابع زیان معیاری است که نشان می‌دهد مقدار حقیقی و مقدار هدف چقدر به هم شباهت دارند؛ بنابراین می‌توان آن را معیار ارزیابی عملکرد الگوریتم دانست. هرچه تابع زیان پایین‌تر باشد، عملکرد مدل بهتر است.

مجدداً یادآوری می‌کنیم که هدف پیدا کردن مقادیری برای weights و bias است که تابع زیان را به حداقل برساند.

حروف J و L در معادله‌ بالا نشان‌دهنده‌ تابع زیان هستند. به تابع زیان، تابع هزینه نیز گفته می‌شود؛ این دو اصطلاح را می‌توان به جای یکدیگر به کار برد.

چطور باید تابع زیان را به حداقل رساند؟

این کار از طریق الگوریتمی به نام گرادیان کاهشی انجام می‌شود.

مفهوم کلی گرادیان کاهشی

در این تصویر،θ_0 همان bias و θ_1 همان weights است.

فرض کنید یک تابع زیان با مختصات J (θ_0,θ_1داریم و می‌خواهیم مقادیری برای θ_0 و θ_1 پیدا کنیم که J را به حداقل برساند. در گرادیان کاهشی، کار را از تعریف تصادفی θ_0 و θ_1 یا جای‌گذاری 0 به جای آن‌ها شروع می‌کنیم. سپس قبل از برداشتن هر قدم به تمام نمای اطراف (360 درجه‌) نگاه می‌کنیم، تا ببینیم برای اینکه هرچه سریع‌تر به نقطه پایین برسیم، آیا باید قدم  کوچکی برداریم  و این قدم را در کدام جهت باید برداریم. پایین‌ترین نقطه‌ تابع جایی است که مقدار J در آنجا به حداقل می‌رسد؛ مختصات آن نقطه مقدارθ_0 و θ_1 را مشخص می‌کند. پس در کل می‌توان گفت که الگوریتم گرادیان کاهشی به دنبال این است که در هر گام، شیب‌دارترین حرکت رو به پایین را انجام دهد.

الگوریتم گرادیان کاهشی

ابتدا پارامترهای weights و bias را به‌صورت تصادفی یا به‌صورت برداری از مقادیر صفر تعریف می‌کنیم:

# Initializing weights as a matrix of zeros of size: (number of 
# features: n, 1) and bias as 0
weights = np.zeros((n,1))
bias = 0

سپس مقدار این پارامترها را به‌صورت پیوسته تغییر می‌دهیم (به‌روزرسانی می‌کنیم) تا تابع زیان L را کاهش دهیم.

قانون به‌روزرسانی برای گرادیان کاهشی

# Updating the parameters: parameter := parameter - lr*(derivative 
# of loss/cost w.r.t parameter)
weights -= lr*dw
bias -= lr*db

lr یا alpha نشان‌دهنده‌ نرخ یادگیری است. این پارامتر اندازه‌ گام رو به پایین را تعیین می‌کند. هرچه نرخ یادگیری پایین‌تر باشد، اندازه‌ گام‌ها باید کوچک‌تر باشد و بالعکس.

در شکل بالا، پارامتر w گام‌های رو به پایین بر می‌دارد، تا به کمینه‌ J برسد. مقداری از w که J در آنجا کمینه می‌شود، مقدار بهینه‌ w است.

گرادیان/مشتق weights با توجه به تابع زیان

dw = (1/m)*np.dot(X.T, (y_hat - y))

گرادیان/مشتق bias با توجه به تابع زیان

db = (1/m)*np.sum((y_hat - y))

اگر سررشته‌ای از مباحث حسابان داشته باشید، می‌توانید مشتق نسبی تابع زیان () را با توجه به پارامترهای weights و bias محاسبه کنید؛ مشاهده خواهید کرد که نتایج یکسان خواهد بود.

خلاصه‌ رگرسیون خطی

ابتدا داده‌ها را از نظر X (ویژگی‌ها) و y (برچسب‌ها) تفکیک کنید. سپس پارامترها را به‌صورت یک مقدار تصادفی یا صفر تعریف کنید.

weights = np.zeros((n,1))  # n: number of features
bias = 0

سپس این گام‌ها را انجام دهید:

H(x) یا y را محاسبه کنید.

weights = np.zeros((n,1))  # n: number of features
bias = 0

گرادیان‌های تابع زیان را با توجه به پارامترهای weights و bias محاسبه کنید.

dw = (1/m)*np.dot(X.T, (y_hat - y))
db = (1/m)*np.sum((y_hat - y))

1. پارامترهای weights و bias را به‌روزرسانی کنید.

weights -= lr*dw
bias -= lr*db

1. گام‌های بالا را تکرار کنید. تعداد دفعات تکرار، تعداد همان گام‌های رو به پایین است؛ در یادگیری ماشینی به این عدد، دوره (یا تعداد تکرار) نیز گفته می‌شود.

کلاس رگرسیون خطی

# Linear Regression classclass LinReg:
    
    # Initializing lr: learning rate, epochs: no. of iterations, 
    # weights & bias: parameters as None    # default lr: 0.01, epochs: 800
    def __init__(self, lr=0.01, epochs=800):
        self.lr = lr
        self.epochs = epochs
        self.weights = None
        self.bias = None    # Training function: fit
    def fit(self, X, y):
        # shape of X: (number of training examples: m, number of    
        # features: n)
        m, n = X.shape    
    
        # Initializing weights as a matrix of zeros of size: (number
        # of features: n, 1) and bias as 0
        self.weights = np.zeros((n,1))
        self.bias = 0
        
        # reshaping y as (m,1) in case your dataset initialized as 
        # (m,) which can cause problems
        y = y.reshape(m,1)
        
        # empty lsit to store losses so we can plot them later 
        # against epochs
        losses = []
        
        # Gradient Descent loop/ Training loop
        for epoch in range(self.epochs):
        
            # Calculating prediction: y_hat or h(x)
            y_hat = np.dot(X, self.weights) + self.bias
     
            # Calculting loss
            loss = np.mean((y_hat - y)**2)
    
            # Appending loss in list: losses
            losses.append(loss)
    
            # Calculating derivatives of parameters(weights, and 
            # bias) 
            dw = (1/m)*np.dot(X.T, (y_hat - y))
            db = (1/m)*np.sum((y_hat - y))   # Updating the parameters: parameter := parameter - lr*derivative
   # of loss/cost w.r.t parameter)
            self.weights -= self.lr*dw
            self.bias -= self.lr*db
        
        # returning the parameter so we can look at them later
        return self.weights, self.bias, losses    # Predicting(calculating y_hat with our updated weights) for the 
    # testing/validation     
    def predict(self, X):
        return np.dot(X, self.weights) + self.bias

آزمایش کلاس LinReg روی دیتاست

آموزش

X_train, X_test, y_train, y_test = X[:20], X[20:], y[:20], y[20:]model = LinReg(epochs=100)
w, b, l = model.fit(X_train,y_train)

نتایج مصورسازی

# Plotting our predictions.fig = plt.figure(figsize=(8,6))
plt.scatter(X, y)
plt.plot(X, model.predict(X))  # X and predictions.
plt.title('Hours vs Percentage')
plt.xlabel('X (Input) : Hours')
plt.ylabel('y (Target) : Scores')

# Predicting on the test set.X_test_preds = model.predict(X_test)
X_test_preds>> array([[28.05459243],
       [48.44728266],
       [38.73647779],
       [68.83997288],
       [77.57969726]])

مقایسه‌ مقادیر حقیقی با پیش‌بینی‌های مدل

# Comparing True values to our predictions.Compare_df = pd.DataFrame({'Actual':y_test,Predicted':X_test_preds})
Compare_df

تابع زیان به‌ازای دوره‌ها (تعداد تکرارها)

fig = plt.figure(figsize=(8,6))
plt.plot([i for i in range(100)], l, 'r-')
plt.xlabel('Number of iterations')
plt.ylabel('Loss / Cost')

همان‌طور که مشاهده می‌کنید با هر گامی که برداشته می‌شود، تابع زیان کمتر و کمتر می‌شود؛ پس در می‌یابیم که جهت حرکت ما در فضای تابع زیاندرست است.