معادلات نرمال در پایتون: راهکاری فرمبسته برای رگرسیون خطی
مقدمات یادگیری ماشینی: قسمت سوم
در این نوشتار، به پیادهسازی معادله نرمالNormal equation میپردازیم که یک راهکار فرمبستهClosed-form solution برای الگوریتم رگرسیون خطی است. با استفاده از معادلات نرمال، میتوانیم مقدار بهینه theta را تنها طی یک مرحله و بدون استفاده از الگوریتم گرادیان کاهشیGradient descent محاسبه کنیم.
در ابتدا مروری بر کلیات الگوریتم گرادیان کاهشی خواهیم داشت. سپس در خصوص محاسبه theta با استفاده از معادله نرمال صحبت خواهیم کرد. در نهایت، اجرای معادله نرمال را توضیح داده و پیشبینیهایی را که روی دیتاست تصادفی انجام دادهایم، مصورسازی میکنیم.
مطالب مجموعه «مقدمات یادگیری ماشینی»:
- رگرسیون خطی در پایتون
- گرسیون خطی با وزن محلیLocally weighted linear regression (وزنی محلی) در پایتون
- معادلات نرمال در پایتون، یک راهکار فرمبسته برای رگرسیون خطی
- رگرسیون چندجملهایPolynomial regression در پایتون
مروری بر گرادیان کاهشی
- x: دادههای ورودی (دادههای آموزشی)
- y: متغیر هدف
- Theta: پارامتر
: پیشبینی/فرضیه (ضرب ماتریسی theta و x)

منبع: geeksforgeeks.org
- تابع زیان: تابع زیان MSE یا خطای میانگین مجذورات (y_hat-y)²

منبع: geeksforgeeks.org
الگوریتم گرادیان کاهشی

ابتدا پارامتر theta را بهصورت تصادفی تعریف کرده یا به همه مقادیر آن 0 میدهیم؛ سپس:
1. فرضیه/پیشبینی y ̂را با استفاده از معادله 1 محاسبه میکنیم؛
2. از فرضیه/پیشبینی y ̂ برای محاسبه تابع زیان MSE استفاده میکنیم: (y_hat-y)²؛
3. سپس مشتق (گرادیان) تابع زیان MSE را نسبت به پارامتر theta محاسبه میکنیم؛
4. در آخر از این مشتق جزئیPartial derivative (گرادیان) برای بهروزرسانی پارامتر theta استفاده میکنیم: theta := theta -lr*gradient. در این فرمول، lr نشاندهنده نرخ یادگیریLearning rate است؛
5. گامهای 1 تا 4 را تکرار میکنیم، تا به مقدار بهینه برای پارامتر theta دست یابیم.
بیشتر بخوانید: رگرسیون خطی با وزن محلی (رگرسیون وزنی محلی) در پایتون
معادله نرمال
گرادیان کاهشی یک الگوریتم تکراریIterative است؛ بدین معنی که باید چندین بار یک سری مراحل را تکرار کنید، تا به بهینه سراسری Global optimum دست یابید و پارامترهای بهینه را پیدا کنید. بااینحال، برای مورد خاص رگرسیون خطی، یک راه وجود دارد که از طریق آن میتوان مقادیر بهینه پارامتر theta را فقط طی یک مرحله محاسبه کرد؛ به عبارت دیگر، با استفاده از این روش، فقط با یک گام به بهینه سراسری میرسیم. این روش، معادلات نرمال هستند. معادلات نرمال تنها برای رگرسیون خطی و نه هیچ الگوریتم دیگری، کاربرد دارند.
معادلات نرمال یک راهکار فرمبسته Closed-form برای الگوریتم رگرسیون خطی هستند؛ یعنی با استفاده از آنها میتوانیم تنها با استفاده از یک فرمول که شامل چند ضرب Matrix multiplication و وارونهسازی Matrix inversion ماتریسی میشود، به پارامترهای بهینه دست پیدا کنیم.
برای به دست آوردن theta، مشتق نسبی تابع زیان MSE (معادله 2) را نسبت به متغیر theta محاسبه میکنیم و آن را مساوی با صفر قرار میدهیم. سپس با اجرای مقداری عملیات جبر خطی، مقدار theta را به دست میآوریم.
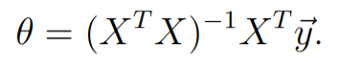
منبع: Andrew Ng
اگر با مشتقگیری ماتریسی و چندین خاصیت دیگر ماتریسها آشنا باشید، میتوانید معادله نرمال را به دست آورید.
برای اطلاعات بیشتر به این لینک مراجعه کنید.
شاید از خود بپرسید اگر X یک ماتریس معکوسناپذیر Non-invertible باشد، باید چه کرد. اگر ویژگیهای زائد داشته باشیم (یعنی ویژگیهایی که احتمالاً به خاطر تکرار، از نظر خطی وابسته هستند) ماتریس معکوسناپذیر خواهد بود. یک راه برای حل این مشکل این است که ویژگیهایی تکراری را پیدا و اصلاح کنید؛ راه دیگر استفاده از تابع np.pinv در NumPy است.
الگوریتم
1. محاسبه theta با استفاده از معادله نرمال
2. استفاده از theta برای پیشبینی
به اشکال x و y دقت کنید، تا معادله با آنها تطابق داشته باشد.
اجرای معادله نرمال
از دادههای پایین که بهصورت تصادفی تولید شدهاند، بهعنوان مثال استفاده میکنیم، تا معادلات نرمال را توضیح دهیم:
import numpy as npnp.random.seed(42)
X = np.random.randn(500,1)
y = 2*X + 1 + 1.2*np.random.randn(500,1)X.shape, y.shape
>>((500, 1), (500,))
در اینجا، 1=n، یعنی ماتریس x تنها 1 ستون دارد و 500=m، یعنی ماتریس x 500 ردیف دارد. بنابراین X ماتریسی به ابعاد (500xm) و y برداری به طول 500 است.

محاسبه تابع Theta
این کد theta را با استفاده از معادله نرمال محاسبه میکند؛ به کامنتها دقت کنید:
def find_theta(X, y):
m = X.shape[0] # Number of training examples.
# reshaping y to (m,1)
y = y.reshape(m,1)
# The Normal Equation
theta = np.dot(np.linalg.inv(np.dot(X.T, X)), np.dot(X.T, y))
return theta
تابع پیشبینی
به کامنتها توجه کنید.
def predict(X):
# Appending a cloumn of ones in X to add the bias term.
X = np.append(X, np.ones((X.shape[0],1)), axis=1)
# preds is y_hat which is the dot product of X and theta.
preds = np.dot(X, theta)
return preds
مصورسازی پیشبینیها
به کامنتها توجه کنید.
# Getting the Value of theta using the find_theta function.
theta = find_theta(X, y)theta
>>array([[1.90949642],
[1.0388102 ]]# Getting the predictions on X using the predict function.
preds = predict(X)# Plotting the predictions.
fig = plt.figure(figsize=(8,6))
plt.plot(X, y, 'b.')
plt.plot(X, preds, 'c-')
plt.xlabel('X - Input')
plt.ylabel('y - target / true')

خط رنگی وسط نقاط مقادیر پیشبینیشده x را نشان میدهد.
بدین ترتیب توانستیم مقادیر بهینه theta را تنها طی یک گام پیدا کنیم. این مقدار بهدستآمده از theta، کمینه سراسریGlobal minima تابع زیان MSE دادههاست.
چه زمانی از معادله نرمال استفاده میکنیم؟
اگر الگوریتمی که میخواهید استفاده کنید، رگرسیون خطی است و
- n (تعداد ویژگیها) کوچک است؛
- m (تعداد نمونههای آموزشی) کوچک و نزدیک 20000 است،
الگوریتم معادله نرمال میتواند گزینه خوبی برای ساخت مدل یادگیری ماشینی به شمار رود.