راهنمای تخصصی شبکه های عصبی گراف در بینایی رایانه‌

پرسش‌هایی که در این بخش از مقاله بررسی می‌شوند:
1. چرا گراف‌ها مفیدند؟
2. چرا تعریف پیچش  convolution در نمودارها کار دشواری است؟
3. چه عاملی باعث تبدیل شبکه عصبی به شبکه عصبی مبتنی بر گراف می‌شود؟

برای پاسخگویی به این پرسش‌ها، به ارائه مقاله‌ها و نمونه‌ها و اسکریپت‌های پایتونی خوبی خواهیم پرداخت تا اطلاعات خوبی درباره شبکه های عصبی گراف یا «GNN»ها به‌دست آورید. انتظار داریم خوانندگان این مقاله، دانش پایه در خصوص یادگیری ماشین و بینایی رایانه‌ داشته باشند. با این حال، یک سری اطلاعات پس‌زمینه‌ای و توضیحات بیشتر در اختیار خوانندگان قرار خواهیم داد. اول از همه، بگذارید به‌طور خلاصه توضیح دهیم که گراف یا نمودار چیست؟

گراف (G)

گراف (G) به مجموعه‌ای از گره‌های به هم‌پیوسته توسط لبه‌ها گفته می‌شود. گره‌ها و لبه‌ها معمولاً از دانش تخصصی در خصوص مسئله مورد نظر نشات می‌گیرند. این مسئله می‌تواند اتم‌های موجود در مولکول‌ها، کاربرانِ یک شبکه اجتماعی، شهرها در سیستم حمل و نقل، بازیکنانِ یک تیم ورزشی، سلول‌های عصبیِ مغز، اجرامِ در حال تعامل در یک سیستم فیزیکیِ پویا، پیکسل‌های یک عکس و… باشد. به عبارت دیگر، در بسیاری از موارد عَملی، این خود کاربران هستند که تصمیم می‎گیرند گره‌ها و لبه‌ها در نمودار چه باشند. این یک ساختار داده‌ایِ بسیار انعطاف‌پذیر است که ساختارهای داده‌ای متعددی را ایجاد می‌کند.

برای مثال، اگر هیچ لبه‌ای وجود نداشته باشد، ساختار به یک مجموعه تبدیل می‌شود؛ اگر فقط لبه‌های عمودی وجود داشته باشد و دو گره دقیقاً توسط یک مسیر به هم وصل شده باشند، ساختار درختی به کارمان می‌آید. این انعطاف‌پذیری می‎تواند مزایا و معایب خود را داشته باشد که جزئیات آن‌ها را در مقاله حاضر بررسی می‌کنیم.

1. چرا گراف‌ها مفیدند؟

در حوزه بینایی رایانه‌ای (CV) و یادگیری ماشین (ML)، مطالعه نمودارها و مدل‌ها برای به‌دست آوردن اطلاعات، می‌تواند دست‌کم چهار مزیت عمده داشته باشد:

• این کار می‌تواند کمک موثری در حل آن دسته از مسائل مهمی باشد که از جمله مسائل چالش‌برانگیز محسوب می‌شدند؛ مثل کشف دارو برای سرطان (وسلکوف و همکارانش، مجله نیچر، 2019)؛ درک بهتر ساختار مغز انسان (دیز و سپلوکر؛ مجله Nature Communications، 2019)؛ کشف مواد برای چالش‌های زیست‌محیطی و انرژی (ژی و همکارانش، مجله Nature Communications، 2019)

• داده‌ها در اکثر حوزه‌های بینایی رایانه‌ (CV) و یادگیری ماشین (ML) به عنوان نمودار در نظر گرفته می‌شوند، اگرچه عادت داریم آن‌ها را به عنوان ساختار داده دیگری در نظر بگیریم. نمایش داده‌ها انعطاف‌پذیری زیادی دارند و دید جالب و متفاوتی درباره مسئله مورد نظر در اختیارمان می‌گذارند. برای مثال، شما می‌توانید به جای یادگیری از پیکسل‌های عکس، از سوپرپیکسل‌ها استفاده کنید. مقاله BMVC هم اطلاعات خوبی در این زمینه فراهم کرده است.

نمودارها این فرصت را به ما می‌دهند تا استدلالی منطقی در خصوص داده‌ها انجام دهیم که باید دانش و اطلاعات قبلی هم درباره آن مسئله داشته باشید. برای مثال، اگر می‌خواهید درباره ژست بدنی یک انسان به استدلال بپردازید، سوگیری منطقی شما می‌تواند نموداری از مفاصل بدن انسان باشد. یا اگر می‌خواهید درباره فیلم‌ها استدلال کنید، باید سوگیری منطقی خود را بر پایه کادرهای متحرک قرار دهید. مثال دیگر، نمایش دادن ویژگی‌های صورت در قالب یک نمودار است تا درباره هویت و ویژگی‌های مختلف چهره به استدلال پردازیم.

• شبکه عصبی مورد علاقه‌تان را هم می‌توانید یک نمودار در نظر بگیرید؛ پس گره‌ها به عنوان سلول‌های عصبی و لبه‌ها به عنوان وزن عمل می‌کنند. به عبارت دیگر، گره‌ها نقش لایه را ایفا کرده و لبه‌ها جریان پس و پیش را نشان می‌دهند. در این مورد، منظورمان یک نمودار محاسباتی است که در تنسورفلو، PyTorch و سایر چارچوب‌های DL استفاده می‌شود. از جمله کاربرد آن می‌توان به بهینه‌سازی نمودار محاسبه، جستجوی معماری عصبی، تجزیه و تحلیل رفتار آموزش و… اشاره کرد.

• در نهایت، می‌توانید مسائل زیادی را حل کنید؛ داده‌ها به شکل موثر و طبیعی‌تری در قالب نمودار به نمایش درمی‌آیند. این مورد می‌تواند در طبقه‌بندی شبکه اجتماعی و مولکولی، طبقه‌بندیِ مِش سه‌بعدی، مدل‌سازیِ رفتار اشیایی که به صورت پویا با هم برهم‌کنش می‌کنند، مدل‌سازی نمودار صحنه بصری (کارگاه ICCV)، پاسخگویی به پرسش، فعالیت‎های یادگیری مختلف  و بسیاری دیگر از مسائل نیز استفاده شود.

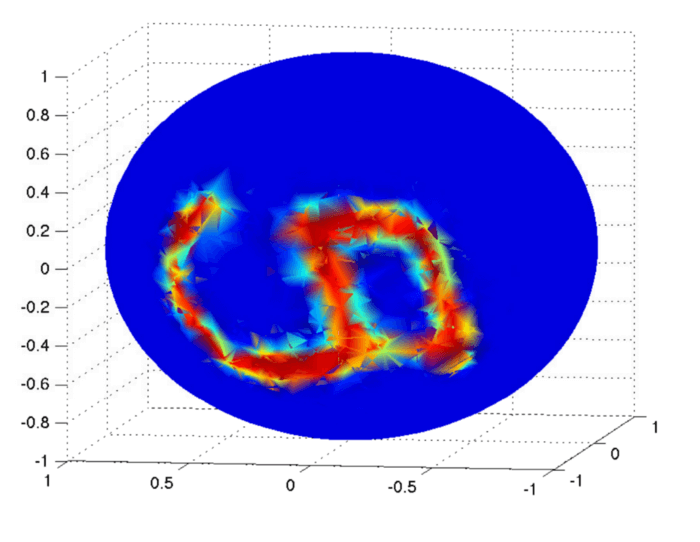
از آنجا که تحقیقات قبلی به تشخیص و تحلیل چهره و عواطف مربوط می‌شود، شکل زیر جزئیاتی در خصوص تحقیقات‌مان را به تصویر می‌کِشد.

در این شکل ، یک چهره در قالب نمودار به نمایش در آمده است. این روش جالبی است، اما در بسیاری از موارد نمی‌تواند تمام ویژگی‌های چهره را پوشش دهد. شبکه‌های پیچشی اطلاعات بسیار زیادی درباره بافت صورت در اختیارمان می‌گذارند. در مقابل، استدلال با مِش‌های سه‌بعدی چهره روش معقول‌تری در مقایسه با روش‌های دوبعدی به حساب می‌آید.

2. چرا تعریف لایه پیچش در نمودارها کار دشواری است؟

برای پاسخگویی به این پرسش، در ابتدا باید به علاقه‌مندان استفاده از شبکه پیچشی انگیزه بدهیم. سپس، «ویژگی‌های پیچشی عکس» را با استفاده از اصطلاح نمودار توضیح دهیم.

چرا لایه پیچشی می‌تواند مفید باشد؟

بگذارید ببینیم چرا پیچش تا این حد می‌تواند برای ما اهمیت داشته باشد و چرا استفاده از آن در نمودارها ضرورت دارد. شبکه‌های پیچشی در مقایسه با شبکه‌های عصبیِ کاملاً به‌هم‌پیوسته دارای مزیت‌های مشخصی هستند که در بخش زیر بر اساس تصویر یک ماشین شورلت قدیمی و زیبا توضیح داده خواهد شد.

اولا، شبکه‌های پیچشی در عکس‌ها ارجحیت طبیعی دارند.

• تغییرناپذیری – جابجایی: اگر خودرویی را که در این عکس مشاهده می‌کنید به چپ، راست، بالا و پایین تصویر حرکت بدهیم، باید کماکان بتوانیم آن را به عنوان یک خودرو تشخیص دهیم. این کار با به‌کارگیری فیلترهایی در تمامی موقعیت‌ها (یعنی استفاده از پیچش) انجام می‌شود.
• ویژگی‌ محلی: پیکسل‌های پیرامون ارتباط نزدیکی با هم دارند و غالباً از نوعی مفهوم معنایی حکایت دارند؛ مثل پیکسل‌های تشکیل دهنده چرخ یا پنجره. این کار با استفاده از فیلترهای نسبتاً بزرگ انجام می‌شود که می‌توانند ویژگی‌های عکس را در محدوده فضایی محلی پوشش دهند.
• حالت ترکیبی (یا سلسله‌مراتبی): ناحیه بزرگتر در عکس غالباً والدین معناییِ نواحی کوچکتر برشمرده می‌شود. برای مثال، خودرو والدین درها، پنجره‌ها، چرخ‌ها، راننده و… می‌باشد. راننده نیز والدین سر، بازو و… است. استفاده از لایه‌های پیچشی و لایه «Pooling» یا ادغام در این راستا کارساز خواهد بود.

در ثانی، تعداد پارامترهای قابل آموزش (مثل فیلترها) در لایه‌های پیچشی به ابعاد ورودی بستگی ندارد و از دیدگاه فنّی، همان مدل را می‌توان در عکس‌های 28 * 28 و 512 * 512 آموزش داد. به عبارتی، مدل حالت پارامتری دارد. در حالت ایده‌آل هدف‌مان ساخت مدلی است که مثل شبکه ‌های عصبی گراف، انعطاف‌پذیری زیاد و قابلیت یادگیری از هر داده‌ای را داشته باشد. در ضمن، می‌خواهیم عوامل موثر در این انعطاف‌پذیری را با بررسی اولویت‌ها کنترل کنیم.

در ایده‌آل‌ترین حالت، هدف ما توسعه مدل یادگیری ماشینی است که به اندازه ساختار شبکه های عصبی گرافی منعطف باشد و بتواند از داده‌ها آموزش ببیند و یاد بگیرد و به طور موازی این قابلیت را داشته باشیم که فاکتورهای مهم را کنترل کنیم و این انعطاف را با خاموش/روشن کردن نورون های عصبی به دست بیاوریم.

تمامی این ویژگی‌ها باعث می‌شوند شبکه‌های پیچشی از بیش‌برازش Locality جلوگیری کنند و مقیاس‌پذیری بالایی در مجموعه‌داده‌ها و عکس‌های بزرگتر داشته باشند. بنابراین، وقتی بخواهیم مسائل مهمی را حل کنیم که در آن‌ها داده‌های ورودی دارای ساختار گرافی هستند، باید همه این ویژگی‌ها را در شبکه های عصبی گراف (نموداری) به کار ببریم تا مقیاس‌پذیری و انعطاف‌پذیری افزایش پیدا کند. در حالت ایده‌آل، هدف‌مان ساخت مدلی است که مثل شبکه ‌های عصبی گراف انعطاف‌پذیری زیادی داشته و قابلیت یادگیری از هر داده‌ای را داشته باشد.

در ضمن، می‌خواهیم عوامل موثر در این انعطاف‌پذیری را با بررسی اولویت‌ها کنترل کنیم. این کار می‌تواند باعث گسترش دامنه تحقیقات شود. با این حال، کنترل این موارد چالش‌برانگیز خواهد بود.

پیچش در عکس‌ها بر حسب گراف ها

نمودار G با گره‌های N را در نظر بگیرید. لبه‌های E نشان‌دهندۀ پیوندهای غیرمستقیم بین گره‌ها است. گره‌ها و لبه‌ها از شهودِ شما درباره مسئله نشات می‌گیرند. شهود ما در مورد عکس‌ها این است که گره‌ها در واقع پیکسل یا سوپرپیکسل (گروهی از پیکسل‌ها با اَشکال عجیب) هستند و لبه‌ها به فواصل فضایی میان آن‌ها گفته می‌شود.

برای مثال، عکس MNIST که در پایین (سمت چپ) مشاهده می‌کنید، در قالب ماتریسی با ابعاد 28 * 28 نشان داده شده است. می‌توانیم آن را به صورت مجموعه N=28*28=784 نیز نشان دهیم. بنابراین، نمودار G دارای 784 گره است و لبه‌ها در صورتی مقادیر بزرگتری خواهند داشت که پیکسل‌ها در نزدیکی آن‌ها باشند. در صورتی هم که پیکسل‌ها در فاصله دوری واقع شده باشند، لبه‌ها مقدار کوچکتری خواهند داشت.

این عکس از مجموعه‌داده MNIST (سمت چپ) گرفته شده است. مثالی از نمایشِ نموداری آن در سمت راست قابل مشاهده است. گره‌های تیره و بزرگ در سمت راست نشان‌دهندۀ شدت بالای پیکسل‌ها است. شکلِ سمت راست از تحقیقات آقای فِی و همکارانش (CVPR، 2018) گرفته شده است.

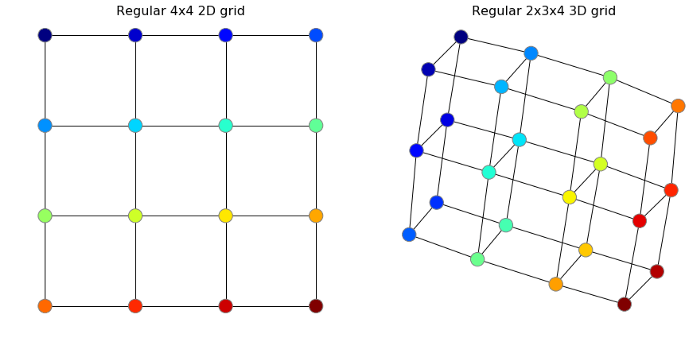
وقتی شبکه‌های عصبی یا «ConvNet»ها را از روی عکس‌ها آموزش می‌دهیم، به‌صورت تلویحی عکس‌ها را روی نمودار تعریف می‌کنیم. از آنجایی که این شبکه در کلیه مراحل آموزش و عکس‌های آزمایشی یکسان است (همه پیکسل‌های شبکه در همه عکس‌ها به شیوه یکسانی به یکدیگر وصل شده‌اند؛ تعداد همسایه‌های یکسانی دارند و…) این نمودار عادی شبکه فاقد اطلاعات مفیدی است که به ما در تفکیک عکس‌ها از یکدیگر کمک کند. چند شبکه عادی دو بعدی و سه بعدی در زیر ملاحظه می‌کنید. ما از «NetworkX» در پایتون برای انجام این کار استفاده کرده‌ایم.

با داشتنِ شبکه عادی 4×4، بگذارید ببینیم پیچش دوبعدی چگونه عمل می‌کند. با این کار می‌توان فهمید که چرا انتقال این اپراتور به نمودارها کار دشواری است. فیلتر در شبکه از تعداد گره‌های یکسانی برخوردار است، اما شبکه‌‎های پیچشی مدرن فیلترهای کوچکی خواهند داشت (مثل 3×3 در مثال زیر). این فیلتر 9 مقدار دارد: W₁,W₂,…, W₉. بر این اساس، W₁,W₂,…, W₉ در طول آموزش با استفاده از پس انتشار back propagation به‌روزرسانی می‌شود تا مسئله حل شود. در مثال زیر، این فیلتر نقش شناساگرِ لبه  edge detector  را ایفا می‌کند.

وقتی مراحل پیچش به انجام می‌رسد، این فیلتر در هر دو جهت به کار برده می‌شود (یعنی به راست و پایین)، اما هیچ‌چیز نمی‌تواند مانع این شود که کار را از گوشه پایین شروع کنیم. حرکت در تمامی جهات ممکن از اهمیت بالایی برخوردار است.

باید در هر مرحله به محاسبه «dot product» یا ضرب نقطه‌ای بین مقادیر شبکه و مقادیر فیلترها W: X₁W₁+X₂W₂+…+X₉W₉ بپردازیم و نتایج را در عکس خروجی ذخیره کنیم. در همین راستا، رنگ گره‌ها را در طول حرکات تغییر می‌دهیم تا با رنگ گره‌ها در شبکه، هم‌خوانی داشته باشد. متاسفانه، همان‌طور که در بخش‌های بعدی توضیح خواهیم داد، این مورد برای همه نمودارها صِدق نمی‌کند.

دو مرحله از پیچش دوبعدی در یک شبکه عادی. اگر عمل لایه‌گذاری (padding) را انجام ندهیم، در مجموع 4 مرحله خواهیم داشت. بنابراین، نتیجۀ کار عکس 2×2 خواهد بود. برای اینکه عکسِ حاصل را بزرگتر کنیم، باید عمل لایه‌گذاری را انجام دهیم. شما می‌توانید از لینک زیر برای کسب اطلاعات جامع در خصوص یادگیری عمیق استفاده کنید.

ضرب نقطه‌ای که در بالا استفاده شد، یکی از aggregator operator عملگرهای تجمیعی Tooltip text می باشد. هدف عملگر تجمیعی این است که داده‌ها را خلاصه کند. در این مثال، ضرب نقطه‌ای ماتریس 3×3 را به یک مقدار خلاصه می‌کند. مثال دیگر، عمل ادغام در شبکه‌های پیچشی است. به خاطر داشته باشید که روش‌هایی از قبیل ادغام بیشینه مقدار یکسانی را در منطقه فضایی ادغام خواهند کرد، حتی اگر همه پیکسل‌ها را بطور تصادفی درون آن مناطق بگنجانید. بگذارید مسئله را شفاف‌تر توضیح دهیم. ضرب نقطه‌ای با تبدیل یا جایگشت تغییرناپذیر است زیرا در کل داریم: X₁W₁+X₂W₂ ≠X₂W₁+X₁W₂

اکنون بگذارید از عکس MNIST برای بررسی معنای شبکه عادی، فیلتر و پیچش استفاده کنیم. اصطلاحات نمودار را در ذهن داشته باشید. این شبکه عادی 28×28 نمودار G ما خواهد بود. لذا هر سلول در این شبکه یک گره به شمار می‌رود. هر گره فقط یک ویژگی خواهد داشت. شدت پیکسل از صفر (سیاه) تا 1 (سفید) متغیر است.

سپس، فیلتری تعریف کرده و آن را فیلتر «Gabor» نام‌گذاری می‌کنیم که چند پارامتر دلخواه دارد. به محض اینکه عکس و فیلتر داشته باشیم، می‌توانیم عمل پیچش را با به‌کارگیری فیلتر در آن عکس انجام دهیم و نتیجۀ ضرب نقطه‌ای را پس از هر مرحله در ماتریس خروجی وارد کنیم.

فیلتر 28×28 (سمت چپ) و نتیجۀ پیچش دوبعدیِ این فیلتر با عکس رقم 7 (سمت راست).

علی‌رغم اینکه این کار مناسب و به‌جا به‌نظر می‌رسد، اما همان‌طور که پیش‌تر اشاره کردم، تعمیم دادنِ پیچش به نمودارها، چالش‌برانگیز است. گره‌ها یک مجموعه هستند و هر گونه تغییر در این مجموعه به تغییر آن مجموعه ختم نمی‌شود. بنابراین، عملگر تجمیعی باید نسبت به تغییرات جایگشتی پایدار  Permutation-invariant باشد.

آن طور که پیش‌تر اشاره کردیم، ضرب نقطه‌ای حساسیت بالایی به بزرگی و مرتبه دارد و این حساسیت خودش را در محاسبه پیچش در هر مرحله، بروز می‌دهد.

این حساسیت اجازه می‌دهد تا اطلاعات خوبی درباره شناساگرهای لبه به‌دست آورده و ویژگی‌های عکس را بشناسیم. مشکل اینجاست که هیچ قانون تعریف‌شده و مشخصی از ترتیب درست گره‌ها در گراف ها وجود ندارد مگر اینکه بتوانیم یک تابع مکاشفه‌ای heuristic function تعریف کنیم تا بهترین حالت را بیابد. در کل، گره‌ها یک مجموعه هستند و هر گونه تغییر در این مجموعه به تغییر آن مجموعه ختم نمی‌شود. به همین دلیل است که باید تابع جمعی نسبت به تغییرات جایگشتی پایدار باشد. بهترین کار این است که از همه همسایه‌ها میانگین بگیریم، یا آن‌ها را جمع ببندیم.

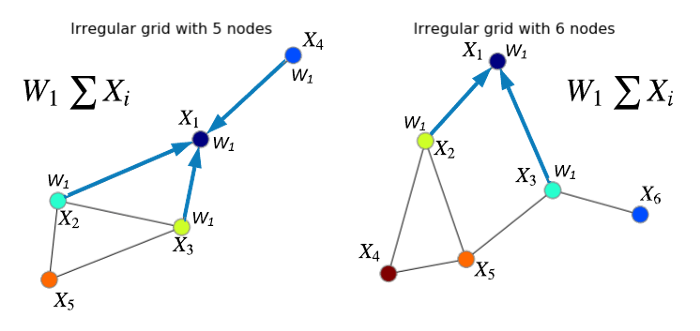
برای نمونه، در نمودار بالا سمت چپ، خروجی مجموع برای گره 1 و گره 2 به ترتیب برابر خواهد بود با: X₁=(X₁+X₂+X₃+X₄) W₁ و X₂=(X₁+X₂+X₃+X₅) W₁. باید از این عملگر جمعی در همه گره‌ها استفاده کنیم. در نتیجه، نموداری با ساختار یکسان به دست خواهد آمد. لذا می‌توان نمودار سمت راست را با استفاده از ایده قبلی پردازش کرد.

معمولاً این را پیچش میانگین یا جمع، نام‌گذاری می‌کنند؛ زیرا از یک گره به گره دیگر رفته و اپراتور اگریگیتور را در هر مرحله به کار می‌بندیم. با این حال، باید این نکته را به خاطر سپرد که ما با نوع خاصی از پیچش سروکار داریم؛ به طوری که فیلترها فاقد جهت‌گیری هستند. در بخش زیر، ویژگی‌های مختلف فیلترها مورد بررسی قرار خواهد گرفت. دستورالعمل‌هایی هم برای بهتر کردن آن‌ها ارائه خواهد شد.

3. چه عاملی باعث تبدیل شبکه عصبی به شبکه های عصبی گراف می‌شود؟

آیا با نحوه عملکرد شبکه عصبی کلاسیک آشنایی دارید؟ ما یک سری ویژگی‌ها با ابعاد C را به عنوان ورودی در شبکه گنجانده‌ایم. با تکیه بر نمونۀ MNIST، X عبارت خواهد بود از C=784. این ویژگی‌ها به وزن W با ابعاد C×F ضرب می‌شوند که در طول آموزش به‌روزرسانی می‌گردد.

هدف از این به‌روزرسانی، رساندنِ خروجی به مقدار دلخواه‌مان است. این نتیجه می‌تواند مستقیماً برای حل مسئله استفاده شده (مانند مسائل regression) یا در اختیار توابع غیرخطی (توابع فعال سازی مانند Relu یا هر تابع مشتق پذیر) قرار گیرد تا یک شبکه چندلایه ایجاد شود.

لایه کاملاً به‌هم‌پیوسته با وزن‌های W. منظور از «به‌هم‌پیوسته» این است که هر مقدار خروجی در X⁽ˡ⁺¹⁾ به همه ورودی‌ها X⁽ˡ⁾ بستگی دارد. یک عبارت بایاس همواره به خروجی اضافه می‌کنیم. اکنون این سوال پیش می‌آید که چگونه شبکه عصبی عادی را می‌توان به شبکه عصبی گراف (نموداری) تبدیل کرد؟

آن‌طور که تا این جای کار می‌دانید، ایده اصلی از به‌کارگیری شبکه های عصبی گراف این است که همسایه‌ها (neighbors) جمع بسته شوند. باید به این نکته توجه داشت که در بسیاری از موارد، این شما هستید که همسایه‌ها را تعیین می‌کنید.
بگذارید یک مورد ساده را در نظر بگیریم. برای مثال، فرض کنید با بخشی از یک شبکه اجتماعی 5 نفره سروکار دارید.

لبه میان جفت‌گره‌ها نشان می‌دهد که آیا دو فرد با هم دوست هستند یا نه. ماتریس مجاورت که معمولاً با حرف A نشان داده می‌شود، راهی برای نشان دادنِ این لبه‌ها در قالب ماتریس است. این روش می‌تواند به راحتی در چارچوب‌های یادگیری عمیق به کار برده شود. سلول‌های زردرنگ در ماتریس، نشان‌دهندۀ لبه هستند و رنگ آبی هم به منزله فقدان لبه است.

نمونه‌ای از یک نمودار و ماتریس مجاورت آن. مرتبه گره‌هایی که در هر دو مورد تعریف شد، تصادفی است، اما گره بدون تغییر باقی مانده است.

حال بیایید بر اساس مختصات پیکسل‌ها، یک ماتریس مجاورت A برای نمونه MNIST بسازیم:

import numpy as np
from scipy.spatial.distance import cdistimg_size = 28 # MNIST image width and height
col, row = np.meshgrid(np.arange(img_size), np.arange(img_size))
coord = np.stack((col, row), axis=2).reshape(-1, 2) / img_size
dist = cdist(coord, coord) # see figure below on the left
sigma = 0.2 * np.pi # width of a Gaussian
A = np.exp(- dist / sigma ** 2) # see figure below in the middle

این تنها روش برای تعریف ماتریس مجاورت نیست (دفراد و همکارانش، NIPS، 2016؛ برونستاین و همکارانش، 2016). این ماتریس مجاورت را بر اساس این اصل که پیکسل‌های مجاور باید به هم وصل شوند و پیکسل‌های دور نباید لبه‌های نازکی داشته باشند، در مدل استفاده می‌کنیم. پیش از این دیدیم که پیکسل‌های نزدیک در عکس‌های طبیعی، غالباً با شیء یا اشیایی مطابقت دارند که به‌طور مکرر در تعامل هستند. لذا پیوند دادن این پیکسل‌ها به هم، منطقی به نظر می‌رسد.

ماتریس مجاورت (N×N) به صورت فاصله (سمت چپ) و نزدیکی (وسط) میان کلیه جفت گره‌ها. در سمت راست گرافی با 16 پیکسل مشاهده می‌کنید. چون این گراف کامل است، به آن دسته یا Clique نیز گفته می‌شود.

بنابراین، به جای اینکه فقط ویژگی‌های X را داشته باشیم، یک ماتریس ویژه A با مقادیری در دامنۀ {1، 0} داریم. باید به این نکته مهم اشاره کرد که وقتی ورودی‌مان را یک نمودار در نظر بگیریم، فرض را بر این می‌گذاریم که گره‌ها فاقد ترتیب متعارف هستند. پس نباید انتظار داشت که گره‌ها در همه نمودارهای موجود در مجموعه‌داده با هم سازگار باشند.

همچنین تصور بر این است که پیکسل‌ها به صورت تصادفی جمع می‌شوند و ترتیب متعارف گره‌ها عملاً غیرممکن است. به خاطر داشته باشید که ماتریسِ ما با ویژگی‌های X دارای N ردیف و C ستون است. بنابراین، از نظر گرافی، هر ردیف نشان‌دهندۀ یک گره و C نشانگرِ ابعاد ویژگی‌های گره است. اما حالا مشکل این است که ترتیب گره‌ها را نمی‌دانیم و مشخص نیست ویژگی‌های یک گره مشخص را باید در کدام ردیف قرار دهیم.

اگر از این مسئله چشم‌پوشی کنیم و X را مستقیماً در MLP به‌کار گیریم (همان کاری که پیشتر انجام دادیم)، همان تاثیری را مشاهده خواهیم کرد که با گنجاندنِ تصادفیِ پیکسل‌ها در عکس‌ها شاهدش بودیم. نکته شگفت‌آور این است که شبکه عصبی می‌تواند کماکان با چنین داده‌های تصادفی تناسب داشته و به کارش ادامه دهد (ژانگ و همکارانش، ICLR، 2017). با این حال، عملکرد آزمایشی به پیش‌بینیِ تصادفی نزدیک خواهد بود. یکی از راه‌حل‌های موجود، استفاده از ماتریس مجاورت A است که به صورت زیر ایجاد می‌شود:

باید از این مسئله اطمینان حاصل کرد که ردیف i حاوی ویژگی‌های گره است. در اینجا باید از ? به جای A استفاده کرد، زیرا معمولاً A نرمال سازی می‌شود. اگر ?=A باشد، ضرب ماتریس ?X⁽ˡ⁾ هم‌ارز با ویژگی‌های جمعی همسایه‌ها خواهد بود. این کار در بسیاری از موارد می‌تواند مفید باشد (ژو و همکارانش، ICLR، 2019). اکنون نوبت به مقایسه NN و GNN به لحاظ کد PyTorch رسیده است. می‌توان از کد PyTorch برای آموزش دو مدل فوق استفاده کرد: python mnist_fc.py –model fc برای آموزش NN و python mnist_fc.py –model graph برای آموزش شبکه های عصبی گراف.

import torch
import torch.nn as nn

C = 2 # Input feature dimensionality
F = 8 # Output feature dimensionality
W = nn.Linear(in_features=C, out_features=F) # Trainable weights

# Fully connected layer
X = torch.randn(1, C) # Input features
Z = W(X) # Output features : torch.Size([1, 8])

#Graph Neural Network layer
N = 6 # Number of nodes in a graph
X = torch.randn(N, C) # Input feature
A = torch.rand(N, N) # Adjacency matrix (edges of a graph)
Z = W(torch.mm(A, X)) # Output features: torch.Size([6, 8])

و این لینک کد کامل نوشته شده با پایتورچ را می توانید برای آموزش مدل جدید به کار ببندید. برای آموزش شبکه عصبی NN ساده از این دستور استفاده کنید:

python mnist_fc.py --model fc

و برای آموزش شبکه عصبی گرافی GNN از این دستور استفاده کنید:

python mnist_fc.py –model graph  برای اینکه این کار را تمرینی انجام دهید، پیکسل‌ها را به‌صورت تصادفی در کد مربوط به –model graph  جای‌گذاری کنید و مطمئن شوید که این کار بر نتیجه تاثیر نگذاشته باشد. شاید بعد از اجرای کد متوجه این نکته شوید که دقت طبقه‌بندی تقریباً یکسان است. پس مشکل کجاست؟ آیا انتظار نمی‌رفت که شبکه‌های گراف عملکرد بهتری داشته باشند؟ خب، این شبکه‌ها در بسیاری از موارد به خوبی عمل می‌کنند.

اما نَه در این مورد، زیرا اپراتور ?X⁽ˡ⁾ فقط یک   فیلتر گائوسی Gaussian filter است، نه هیچ چیز دیگر. بنابراین، مشخص شد که شبکه عصبیِ گراف ما کارکردی برابر با شبکه عصبی پیچشی دارد و به یک فیلتر گائوسی مجهز است که هیچ‌گاه آن را در طول آموزش به‌روزرسانی نمی‌کنیم.

نمایش دوبعدی فیلتر استفاده شده در شبکه عصبی گرافی و تاثیر آن بر عکس

From __future__ import print_function
import argparse
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torchvision import datasets, transforms
import numpy as np
from scipy.spatial.distance import cdist

class BorisNet(nn.Module):
def __init__(self):
super(BorisNet, self).__init__()
self.fc = nn.Linear(784, 10, bias=False)

def forward(self, x):
return self.fc(x.view(x.size(0), -1))

class BorisConvNet(nn.Module):
def __init__(self):
super(BorisConvNet, self).__init__()
self.conv = nn.Conv2d(1, 10, 28, stride=1, padding=14)
self.fc = nn.Linear(4 * 4 * 10, 10, bias=False)

def forward(self, x):
x = F.relu(self.conv(x))
x = F.max_pool2d(x, 7)
return self.fc(x.view(x.size(0), -1))

class BorisGraphNet(nn.Module):
def __init__(self, img_size=28, pred_edge=False):
super(BorisGraphNet, self).__init__()
self.pred_edge = pred_edge
N = img_size ** 2
self.fc = nn.Linear(N, 10, bias=False)
if pred_edge:
col, row = np.meshgrid(np.arange(img_size), np.arange(img_size))
coord = np.stack((col, row), axis=2).reshape(-1, 2)
coord = (coord - np.mean(coord, axis=0)) / (np.std(coord, axis=0) + 1e-5)
coord = torch.from_numpy(coord).float() # 784,2
coord = torch.cat((coord.unsqueeze(0).repeat(N, 1, 1),
coord.unsqueeze(1).repeat(1, N, 1)), dim=2)
#coord = torch.abs(coord[:, :, [0, 1]] - coord[:, :, [2, 3]])
self.pred_edge_fc = nn.Sequential(nn.Linear(4, 64),
nn.ReLU(),
nn.Linear(64, 1),
nn.Tanh())
self.register_buffer('coord', coord)
else:
# precompute adjacency matrix before training
A = self.precompute_adjacency_images(img_size)
self.register_buffer('A', A)

@staticmethod
def precompute_adjacency_images(img_size):
col, row = np.meshgrid(np.arange(img_size), np.arange(img_size))
coord = np.stack((col, row), axis=2).reshape(-1, 2) / img_size
dist = cdist(coord, coord)
sigma = 0.05 * np.pi

# Below, I forgot to square dist to make it a Gaussian (not sure how important it can be for final results)
A = np.exp(- dist / sigma ** 2)
print('WARNING: try squaring the dist to make it a Gaussian')

A[A < 0.01] = 0
A = torch.from_numpy(A).float()

# Normalization as per (Kipf & Welling, ICLR 2017)
D = A.sum(1) # nodes degree (N,)
D_hat = (D + 1e-5) ** (-0.5)
A_hat = D_hat.view(-1, 1) * A * D_hat.view(1, -1) # N,N

# Some additional trick I found to be useful
A_hat[A_hat > 0.0001] = A_hat[A_hat > 0.0001] - 0.2

print(A_hat[:10, :10])
return A_hat

def forward(self, x):
B = x.size(0)
if self.pred_edge:
self.A = self.pred_edge_fc(self.coord).squeeze()

avg_neighbor_features = (torch.bmm(self.A.unsqueeze(0).expand(B, -1, -1),
x.view(B, -1, 1)).view(B, -1))
return self.fc(avg_neighbor_features)

def train(args, model, device, train_loader, optimizer, epoch):
model.train()
for batch_idx, (data, target) in enumerate(train_loader):
data, target = data.to(device), target.to(device)
optimizer.zero_grad()
output = model(data)
loss = F.cross_entropy(output, target)
loss.backward()
optimizer.step()
if batch_idx % args.log_interval == 0:
print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
epoch, batch_idx * len(data), len(train_loader.dataset),
100. * batch_idx / len(train_loader), loss.item()))

def test(args, model, device, test_loader):
model.eval()
test_loss = 0
correct = 0
with torch.no_grad():
for data, target in test_loader:
data, target = data.to(device), target.to(device)
output = model(data)
test_loss += F.cross_entropy(output, target, reduction='sum').item()
pred = output.argmax(dim=1, keepdim=True)
correct += pred.eq(target.view_as(pred)).sum().item()

test_loss /= len(test_loader.dataset)

print(
'\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
test_loss, correct, len(test_loader.dataset),
100. * correct / len(test_loader.dataset)))

def main():
# Training settings
parser = argparse.ArgumentParser(description='PyTorch MNIST Example')
parser.add_argument('--model', type=str, default='graph', choices=['fc', 'graph', 'conv'],
help='model to use for training (default: fc)')
parser.add_argument('--batch-size', type=int, default=64,
help='input batch size for training (default: 64)')
parser.add_argument('--test-batch-size', type=int, default=1000,
help='input batch size for testing (default: 1000)')
parser.add_argument('--epochs', type=int, default=10,
help='number of epochs to train (default: 10)')
parser.add_argument('--lr', type=float, default=0.001,
help='learning rate (default: 0.001)')
parser.add_argument('--pred_edge', action='store_true', default=False,
help='predict edges instead of using predefined ones')
parser.add_argument('--seed', type=int, default=1,
help='random seed (default: 1)')
parser.add_argument('--log-interval', type=int, default=200,
help='how many batches to wait before logging training status')

args = parser.parse_args()
use_cuda = True

torch.manual_seed(args.seed)

device = torch.device("cuda" if use_cuda else "cpu")

kwargs = {'num_workers': 1, 'pin_memory': True} if use_cuda else {}
train_loader = torch.utils.data.DataLoader(
datasets.MNIST('../data', train=True, download=True,
transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])),
batch_size=args.batch_size, shuffle=True, **kwargs)
test_loader = torch.utils.data.DataLoader(
datasets.MNIST('../data', train=False, transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])),
batch_size=args.test_batch_size, shuffle=False, **kwargs)

if args.model == 'fc':
assert not args.pred_edge, "this flag is meant for graphs"
model = BorisNet()
elif args.model == 'graph':
model = BorisGraphNet(pred_edge=args.pred_edge)
elif args.model == 'conv':
model = BorisConvNet()
else:
raise NotImplementedError(args.model)
model.to(device)
print(model)
optimizer = optim.SGD(model.parameters(), lr=args.lr, weight_decay=1e-1 if args.model == 'conv' else 1e-4)
print('number of trainable parameters: %d' %
np.sum([np.prod(p.size()) if p.requires_grad else 0 for p in model.parameters()]))

for epoch in range(1, args.epochs + 1):
train(args, model, device, train_loader, optimizer, epoch)
test(args, model, device, test_loader)

if __name__ == '__main__':
main()
# Examples:
# python mnist_fc.py --model fc
# python mnist_fc.py --model graph
# python mnist_fc.py --model graph --pred_edge

این فیلتر اساساً عکس را شفاف یا تار می‌کند که البته کار چندان مفیدی نیست. با وجود این، شبکه عصبیِ گراف ساده‌ترین نوع شبکه عصبی گراف به شمار می‌رود که عملکرد بسیار درخشانی در داده‎‌های نموداری دارد. برای اینکه شبکه های عصبی گراف به شکل بهتری در نمودارهای عادی عمل کند، باید از چند ترفند استفاده کنیم. برای مثال، به جای استفاده از فیلتر گائوسیِ از پیش تعریف‌شده، باید یاد بگیریم لبه‌ای را میان هر جفت پیکسلی پیش‌بینی کنیم. در این راستا، می‌توان از تابع زیر استفاده کرد:

import torch.nn as nn # using PyTorchnn.Sequential(nn.Linear(4, 64), # map coordinates to a hidden layer
nn.ReLU(), # nonlinearity
nn.Linear(64, 1), # map hidden representation to edge
nn.Tanh()) # squash edge values to [-1, 1]

فیلتر دوبعدی شبکه عصبی گراف که در مرکز قرار دارد و با نقطه قرمز رنگ دیده شده است.
برای ساخت این گیف‌ها می‌توانید از کد زیر استفاده کنید:

import imageio # to save GIFs
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
from scipy.spatial.distance import cdist
import cv2 # optional (for resizing the filter to look better)

img_size = 28
# Create/load some adjacency matrix A (for example, based on coordinates)
col, row = np.meshgrid(np.arange(img_size), np.arange(img_size))
coord = np.stack((col, row), axis=2).reshape(-1, 2) / img_size
dist = cdist(coord, coord) # distances between all pairs of pixels
sigma = 0.2 * np.pi # width of a Gaussian (can be a hyperparameter when training a model)

A = np.exp(- dist / sigma ** 2) # adjacency matrix of spatial similarity
# above, dist should have been squared to make it a Gaussian (forgot to do that)

scale = 4
img_list = []
cmap = mpl.cm.get_cmap('viridis')
for i in np.arange(0, img_size, 4): # for every row with step 4
for j in np.arange(0, img_size, 4): # for every col with step 4
k = i*img_size + j
img = A[k, :].reshape(img_size, img_size)
img = (img - img.min()) / (img.max() - img.min())
img = cmap(img)
img[i, j] = np.array([1., 0, 0, 0]) # add the red dot
img = cv2.resize(img, (img_size*scale, img_size*scale))
img_list.append((img * 255).astype(np.uint8))
imageio.mimsave('filter.gif', img_list, format='GIF', duration=0.2)

نتیجه‌گیری

شبکه های عصبی گراف به دسته‌ای جالب و انعطاف‌پذیر از شبکه‌های عصبی گفته می‌شود که امکان استفاده از آن‌ها در داده‌های پیچیده وجود دارد. این سطح از انعطاف‌پذیری مثل همیشه هزینه‌هایی در پی دارد.

در شبکه های عصبی گراف، عادی‌سازیِ مدل با تعریف عملگرهایی مثل لایه های پیچشی، خیلی دشوار می‌شود. تحقیقات در این حوزه با سرعت در جریان است و محققان ابراز امیدواری کرده‌اند که شبکه های عصبی گراف کاربرد فزاینده‌ای در طیف وسیعی از حوزه‌های یادگیری ماشین و بینایی رایانه‌ خواهند داشت.