3 الگوریتم تشخیص داده پرت که هر متخصص علوم دادهای به آنها نیاز دارد
برای آنکه به درک روشنی از تشخیص داده پرت برسید و نحوه پیادهسازی سه الگوریتم ساده و در عین حال قوی تشخیص داده پرت در پایتون را یاد بگیرید، تا پایان این مقاله با ما همراه باشید.
به طور قطع میتوانم بگویم مشکلاتی از این قبیل برای شما هم پیش آمده است:
- مدل شما آنگونه که انتظار داشتید، عمل نمیکند.
- برخی از دادهها تفاوتهای چشمگیری با سایر دادهها دارند و برای حل این مشکل راهحل به ذهن شما نمیرسد.
|| مسابقه هوش مصنوعی (مهلت ثبتنام تا 16 آذر 1401)
منظور از داده پرت چیست؟

در آمار، داده پرت به دادهای گفته میشود که تفاوت چشمگیری با سایر مشاهدات (دادهها) دارد. همانگونه که در تصویر فوق مشاهده میکنید، اکثر نقاط یا بر روی ابرصفحه خطی قرار دارند یا در اطراف آن، اما یک نقطه از سایر نقاط فاصله دارد. به این نقطه، داده پرت گفته میشود.
برای نمونه، نگاهی به فهرست مقابل بیندازید:
[1,35,20,32,40,46,45,4500]
اعداد 1 تا 4500 این دیتاست، داده پرت هستند.
دلایل وجود داده پرت
معمولاً، دادههای پرت به دلایلی که در ادامه به آنها اشاره خواهیم کرد، شکل میگیرند:
- برخی مواقع به صورت تصادفی، احتمالاً در نتیجه خطای اندازهگیری ایجاد میشوند.
- احتمال وجود دادههایی که 100% خالص باشند و هیچگونه داده پرتی در آنها وجود نداشته باشد، بسیار کم است.
چرا دادههای پرت به نوعی چالش به حساب میآیند؟
برخی دلایل آن عبارتند از:
1- مدلهای خطی
فرض کنید دادههایی دارید و قصد دارید بر مبنای این دادهها و با استفاده از رگرسیون خطی، قیمت مسکن را پیشبینی کنید. یکی از فرضیههای احتمالی میتواند بدین شکل باشد:

در این حالت، در واقع دادهها را به خوبی برازش میکنیم (بیش برازش). البته اگر به دقت به نمودار بالا نگاه کنید، متوجه میشوید که تمامی نقاط در یک محدوده واحد قرار دارند.
حالا میخواهیم ببینیم اگر یک داده پرت اضافه کنیم، چه اتفاقی میافتد:

به خوبی میبینیم که با افزودن یک داده پرت، موقعیت سایر دادهها تغییر میکند و فرضیه ما تغییر میکند و در نتیجه استنباط نسبت به زمانی که در دادهها داده پرت وجود نداشت، دشوارتر خواهد بود. مدلهای خطی موارد زیر را شامل میشوند:
- پرسپترون
- رگرسیون خطی و رگرسیون لجیستیک
- شبکههای عصبی
- کی نزدیکترین همسایه (KNN)
2- جانهی دادهها

یکی از مشکلات رایجی که ممکن است پیش بیاید، فقدان دادهها است و در مواجه با آن میتوانید دو رویکرد اتخاذ کنید:
1- نمونهها را به همراه ردیفهای گمشده حذف کنید.
2- (مقادیر) را با استفاده از روشهای آماری جایگزین دادههای گمشده کنید.
از آنجاییکه دادههای پرت میتوانند تا حد زیادی مقادیر روشهای آماری را تغییر دهند، اگر رویکرد دوم را اتخاذ کنیم، برای جانهی دادهها با مشکل مواجه خواهیم شد. برای درک بهتر موضوع تشخیص داده پرت، برای مثال، بیایید دوباره دادههای ساختگی بدون داده پرت را با یکدیگر بررسی کنیم:
# Data with no outliers np.array([35,20,32,40,46,45]).mean() = 36.333333333333336# Data with 2 outliers np.array([1,35,20,32,40,46,45,4500]).mean() = 589.875
بدیهی است که تشابه میان این دو مجموعهداده مبالغهآمیز است و وجود دادههای پرت در دادهها اغلب مشکلساز است و اینگونه دادهها میتوانند مشکلات جدی در مدلسازی و تحلیل آماری به وجود بیاورند. در این مقاله قصد داریم روشهای تشخیص و مقابله با دادههای پرت با یکدیگر را بررسی کنیم.
روشهای تشخیص و مقابله با دادههای پرت با یکدیگر
راهحل اول: DBSCAN

خوشه بندی مکانی داده های دارای نویز بر مبنای چگالی ( به اختصار DBSCAN) همانند k-میانگین، یک الگوریتم خوشهبندی بدون نظارت است. از این الگوریتم میتوان برای تشخیص دادههای پرت استفاده کرد.
یکی از دلایل محبوبیت DBSCAN این است که میتواند خوشههای غیرخطی قابل تفکیک Non-linearly separable clusters
را پیدا کند، در حالیکه الگوریتم k-میانگین و مدل مخلوط گوسی قادر به انجام این کار نیستند. زمانیکه خوشهها به اندازه کافی متراکم هستند و به وسیله نواحی با چگالی پایین از یکدیگر جدا شدهاند، الگوریتم DBSCAN عملکرد خوبی دارد.
مروری بر نحوه عملکرد الگوریتم DBSCAN
الگوریتم DBSCAN، خوشهها را نواحیای پیوسته با چگالی بالا در نظر میگیرد. نحوه عملکرد این الگوریتم بسیار ساده است:
1- برای هر یک از نمونهها، تعداد نمونههایی که در فاصله ε (اپسیلون) از آن قرار دارند را محاسبه میکند. این ناحیه، همسایگی ε نمونه نامیده میشود.
2- چنانچه تعداد نمونههایی که در همسایگی ε نمونه قرار دارند بیشتر از min-samples باشد، این نمونه، نمونه مرکزی در نظر گرفته میشود. نمونه مرکزی به نمونهای اطلاق میشود که در ناحیهای با چگالی بالا قرار دارد ( ناحیهای که نمونههای زیادی در آن قرار دارند).
3- تمامی نمونههایی که در همسایگی ε نمونه مرکزی قرار دارند، به همان خوشه تعلق میگیرند. ممکن است در همسایگی ε نقطه مرکزی، بیش از یک نقطه مرکزی وجود داشته باشد، بنابراین، یک توالی طولانی از نمونههای مرکزی همسایه، یک خوشه واحد را تشکیل میدهد.
4- نمونههایی که نمونه مرکزی نیستند و یا در همسایگی ε نقطه مرکزی قرار ندارند، دادهپرت در نظر گرفته میشوند.
الگوریتم DBSCAN در عمل
API کتابخانه Scikit-Learn استفاده از الگوریتم DBSCAN را بسیار آسان کرده است. در ادامه میتوانید نمونهای از این الگوریتم را مشاهده کنید:
from sklearn.cluster import DBSCAN from sklearn.datasets import make_moonsX, y = make_moons(n_samples=1000, noise=0.05) dbscan = DBSCAN(eps=0.2, min_samples=5) dbscan.fit(X)
یک نمونه اولیه از DBSCAN میسازیم و همسایگی ε را برابر با 0.05 قرار میدهیم و حداقل نمونههای لازم برای اینکه یک نمونه، نمونه مرکزی در نظر گرفته شود برابر 5 است.
همانگونه که پیش از این نیز گفتیم، الگوریتم DBSCAN، یک الگوریتم بدون نظارت است و به همین دلیل، در هنگام کار با این الگوریتم نیازی به برچسبگذاری نیست. برچسبهایی که الگوریتم DBSCAN تولید کرده است را میتوانیم با اجرای دستور مقابل مشاهده کنیم:
dbscan.labels_ OUT: array([ 0, 2, -1, -1, 1, 0, 0, 0, ..., 3, 2, 3, 3, 4, 2, 6, 3])
همانگونه که مشاهده میکنید، مقدار برخی از برچسبها برابر با 1- است، این دادهها، داده پرت هستند.
الگوریتم DBSCAN متد پیشبینی ندارد، بلکه فقط یک متد fit-predict دارد؛ به عبارت دیگر این الگوریتم نمیتواند نمونههای جدید را خوشهبندی کند. در عوض میتوانیم از یک کلاسیفایر متفاوت برای آموزش و پیشبینی استفاده کنیم. برای مثالی که ذکر کردیم میتوانیم از KNN استفاده کنیم:
from sklearn.neighbors import KneighborsClassifier knn = KNeighborsClassifier(n_neighbors=50) knn.fit(dbscan.components_, dbscan.labels_[dbscan.core_sample_indices_]) X_new = np.array([[-0.5, 0], [0, 0.5], [1, -0.1], [2, 1]]) knn.predict(X_new) OUT: array([1, 0, 1, 0])
در این قسمت کلاسیفایر KNN را با نمونههای مرکزی و همسایههای آنها آموزش میدهیم.
اما مشکلی که با آن مواجه میشویم این است که در دادههایی که به KNN دادهایم، داده پرت وجود ندارد و همین مسئله موجب میشود KNN خوشهای را برای نمونههای جدید انتخاب کند، حتی اگر نمونه جدید یک داده پرت باشد.
متد همسایههای k کلاسیفایر KNN میتواند در حل این مشکل به ما کمک کند. اگر مجموعهای از نمونهها را به این KNN بدهیم، این کلاسیفایر فاصلهها و اندیسهای k نزدیک ترین همسایه مجموعه آموزشی را برای ما پیدا میکند. حتی میتوانیم حداکثر فاصله را تعیین کنیم و اگر فاصله نمونهای بیشتر از آن باشد، این نمونه، یک داده پرت خواهد بود.
y_dist, y_pred_idx = knn.kneighbors(X_new, n_neighbors=1) y_pred = dbscan.labels_[dbscan.core_sample_indices_][y_pred_idx] y_pred[y_dist > 0.2] = -1 y_pred.ravel() OUT: array([-1, 0, 1, -1])
در این بخش نحوه پیادهسازی الگوریتم DBSCAN برای تشخیص ناهنجاری را با یکدیگر بررسی کردیم. الگوریتم DBSCAN بسیار سریع است و فقط دو ابرپارامتر دارد و در تشخیص دادههای پرت عملکرد فوقالعادهای دارد.
راهحل دوم: IsolationForest

IsolationForest یک الگوریتم یادگیری جمعی برای تشخیص ناهنجاری است. این الگوریتم در تشخیص دادههای پرتی که در دیتاستهایی با ابعاد زیاد قرار دارند، عملکرد فوقالعادهای دارد. نحوه عملکرد این الگوریتم به شرح زیر است:
1- یک جنگل تصادفی ایجاد میکند که درختهای تصمیم به صورت تصادفی در آن رشد میکنند: در هر یک از گرهها، ویژگیها به صورت تصادفی انتخاب میشوند و سپس IsolationForest یک مقدار آستانه تصادفی انتخاب میکند تا دیتاست را به دو بخش تقسیم کند.
2- این الگوریتم تا زمانیکه تمامی نمونهها از یکدیگر جدا شوند، به تقسیم کردن دیتاست ادامه میدهد.
3- ناهنجاری معمولاً با سایر نمونهها فاصله زیادی دارد، در نتیجه، به طور متوسط ( در تمامی درختهای تصمیم) زودتر از نمونههای معمولی جدا میشود.
IsolationForest در عمل
API کتابخانه Scikit-learn موجب شده پیادهسازی کلاس IsolationForest آسان شود. در ادامه مثالی از این الگوریتم آوردهایم:
from sklearn.ensemble import IsolationForest from sklearn.metrics import mean_absolute_error import pandas as pd
برای اندازهگیری خطا نیز از میانگین قدر مطلق خطا استفاده خواهیم کرد. برای دادهها هم از یکی از دیتاستهای Gitub جیسون برونلیجیسون برونلی Jason Brownlee استفاده میکنیم:
url='https://raw.githubusercontent.com/jbrownlee/Datasets/master/housing.csv' df = pd.read_csv(url, header=None) data = df.values # split into input and output elements X, y = data[:, :-1], data[:, -1]
پیش از آموزش الگوریتم IsolationForest ، دادهها را به مدل استاندارد رگرسیون خطی Vanilla Linear Regression model آموزش میدهیم و MAE را به دست میآوریم:
from sklearn.linear_model import LinearRegression lr = LinearRegression() lr.fit(X,y) mean_absolute_error(lr.predict(X),y) OUT: 3.2708628109003177
امتیاز نسبتاً خوبی است! حالا باید ببینیم آیا Isolation Forest میتواند با حذف ناهنجاریها، این امتیاز را افزایش دهد یا خیر!
ابتدا، IsolationForest مقداردهی اولیه میکنیم:
iso = IsolationForest(contamination='auto',random_state=42)
مهمترین ابرپارامتر این الگوریتم احتمالاً پارامتر Contamination است که از آن برای برآورد تعداد دادههای پرتی که در یک دیتاست وجود دارند، استفاده میشود. تعداد دادههای پرت موجود در یک دیتاست مقداری بین 0.0 و 0.05 است و به صورت پیشفرض 0.1 تعیین میشود.
این الگوریتم در واقع یک Random Forest تصادفی شده است، بنابراین تمامی ابرپارمترهای یک Random Forest را میتوان در این الگوریتم به کار برد.
در گام بعد برای تشخیص داده پرت، دادهها را به الگوریتم آموزش میدهیم:
y_pred = iso.fit_predict(X,y) mask = y_pred != -1
مقادیر پیشبینی شدهای که برابر با 1- هستند را حذف میکنیم. این مقادیر داده پرت به شمار میآیند.
سپس X و Y را با دادههایی که در آنها داده پرت وجود ندارد، دوباره مقداردهی میکنیم:
X,y = X[mask,:],y[mask]
در این مرحله مدل رگرسیون خطی را با دادهها آموزش میدهیم و MAE را محاسبه میکنیم:
lr.fit(X,y) mean_absolute_error(lr.predict(X),y) OUT: 2.643367450077622
همانگونه که مشاهده میکنید، هزینه تا حد زیادی کاهش یافته است. این کاهش هزینه به خوبی قدرت الگوریتم Isolation Forest را نشان میدهد.
راهحل سوم: نمودار جعبهای و روش توکی
هرچند Boxplots روش رایج و محبوبی برای تشخیص ناهنجاریها است، اما آنچنان که باید به روش توکی برای تشخیص دادههای پرت توجه نشده است. پیش از معرفی روش توکی، مروری خواهیم داشت بر Boxplots:
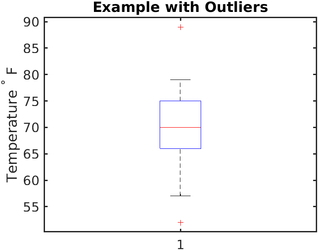
Boxplotها برای نمایش دادههای عددی در چارکها، جعبهای با خطوط ترسیم میکند. این روش بسیار ساده و در همان حال برای نشان دادن دادههای پرت بسیار مؤثر است.
خطوط (whiskers) بالا و پایین محدوده یک توزیع را مشخص میکنند و هر چیزی که در بالا و یا پایین این خطوط قرار بگیرد، داده پرت در نظر گرفته میشود. برای درک بهتر تشخیص داده پرت در نظر داشته باشید که در تصویر بالا، تمامی دادههایی که بالای (به طور تقریبی) 80 و پایین (به طور تقریبی) 62 قرار بگیرد، داده پرت است.
نحوه عملکرد Boxplot
در قدم اول، نمودار جعبهای، دیتاست را به 5 بخش تقسیم میکنید:

- مینیمم: پایینترین نقطه دادههای موجود در توزیع به استثنای دادههای پرت.
- ماکسیمم: بالاترین نقطه دادههای موجود در توزیع به استثنای دادههای پرت.
- میانه (چارک دوم/پنجاهمین صدک): مقدار میانی دیتاست.
- صدک اول (چارک اول/بیستوپنجمین صدک): میانه نیمه پایین دیتاست.
- صدک سوم ( چارک سوم/هفتادوپنجمین صدک): میانه نیمه بالایی دیتاست.
اهمیت دامنه بین چارکی در این است که دادههای پرت را مشخص میکند. IQR به شکل زیر است:
IQR = Q3 - Q1 Q3: third quartile Q1: first quartile
در نمودارهای جعبهای، فاصله 1.5 برابری IQR محاسبه میشود و نقطهدادههایی که در قسمت فوقانی دیتاست قرار دارند، را در بر میگیرد. به همین ترتیب، فاصله 1.5 برابری IQR نقطهدادههایی که در قسمت پایین دیتاست مشاهده میشوند، محاسبه میشود. به بیان دقیقتر:
- اگر نقاط مشاهده شده پایین از (Q1 – 1.5 * IQR) یا خط پایینی نمودار جعبهای باشند، داده پرت به حساب میآیند.
- اگر نقاط مشاهدهشده بالای (Q3 +1.5 * IQR) یا خط فوقانی نمودار جعبهای باشند، داده پرت به حساب میآیند.

نمودار جعبهای در عمل
در این قسمت میخواهیم ببینیم چگونه میتوان با استفاده از نمودارهای جعبهای در پایتون، دادههای پرت را تشخیص داد:
import matplotlib.pyplot as plt import seaborn as sns import numpy as np X = np.array([45,56,78,34,1,2,67,68,87,203,-200,-150]) y = np.array([1,1,0,0,1,0,1,1,0,0,1,1])
اکنون نمودار جعبهای دادهها را ترسیم میکنیم:
sns.boxplot(X) plt.show()

همانگونه که در نمودار جعبهای فوق نشان داده شده است، میانه برابر با 50 است و سه تشخیص داده پرت در دادههای ما وجود دارد. برای حذف کردن این نقاط:
X = X[(X < 150) & (X > -50)] sns.boxplot(X) plt.show()

در اینجا من یک آستانه تعیین کردهام، بنابراین تمامی نقاط کمتر از 50- و بیشتر از 150 حذف خواهند شد و در پایان یک توزیع متوازن خواهیم داشت.
روش توکی برای تشخیص دادههای پرت
روش توکی نمونه غیر بصری نمودار جعبهای است: این روش مشابه نمودار جعبهای است با این تفاوت که در این روش دادههای مصورسازی نمیشوند.
دلیل اینکه گاهی اوقات این روش را بر روش نمودار جعبهای ترجیح میدهم این است که برخی مواقع نگاه کردن به نمودارهایی که بر مبنای دادهها ترسیم شدهاند و تخمین دقیق آستانه کمک چندانی به ما در تشخیص دادههای پرت نمیکند.
در عوض میتوانیم الگوریتمی را کدنویسی کنیم که نمونههایی را که تشخیص میدهد تشخیص داده پرت هستند به ما نشان دهد.
کد پیادهسازی این الگوریتم را در مقابل میتوانید مشاهده کنید:
import numpy as np
from collections import Counter
def detect_outliers(df, n, features):
# list to store outlier indices
outlier_indices = []
# iterate over features(columns)
for col in features:
# Get the 1st quartile (25%)
Q1 = np.percentile(df[col], 25)
# Get the 3rd quartile (75%)
Q3 = np.percentile(df[col], 75)
# Get the Interquartile range (IQR)
IQR = Q3 - Q1
# Define our outlier step
outlier_step = 1.5 * IQR
# Determine a list of indices of outliers
outlier_list_col = df[(df[col] < Q1 - outlier_step) | (df[col] > Q3 + outlier_step)].index
# append outlier indices for column to the list of outlier indices
outlier_indices.extend(outlier_list_col)
# select observations containing more than 2 outliers
outlier_indices = Counter(outlier_indices)
multiple_outliers = list(k for k, v in outlier_indices.items() if v > n)
return multiple_outliers
# detect outliers from list of features
list_of_features = ['x1', 'x2']
# params dataset, number of outliers for rejection, list of features
Outliers_to_drop = detect_outliers(dataset, 2, list_of_features)
نحوه عملکرد این کد بدین شرح است:
1- برای هر یک از ویژگیها:
- صدک اول
- صدک سوم
- IQR
را محاسبه میکند.
2- سپس فاصله داده پرت Outlier step را تعریف میکند؛ این فاصله همانند نمودارهایهای جعبهای برابر با 1.5*IQR است.
3- دادههای پرت را به روشهای زیر شناسایی میکند:
- نقطه مشاهده شده کمتر از Q1 منهای فاصله داده پرت باشد
- نقطه مشاهده شده بیشتر از Q3 به اضافه فاصله داده پرت باشد
4- سپس مشاهداتی که k داده پرت دارند را انتخاب میکند ( در این مورد k برابر با 2 است).