یادگیری ماشین بدون‌ نظارت: تحلیل انواع الگوریتم خوشه بندی

در مقالات آموزشی قبل به معرفی  الگوریتم‌های یادگیری ماشین بانظارت و آن دسته از روش‌های توسعه مدل‌ پرداختیم که در آن‌ها از داده‌های برچسب‌دار استفاده می‌شود. به بیانی دیگر در این دسته از روش‌ها، داده‌ها دارای تعدادی متغیر هدف Target variable با مقادیر مشخص هستند که از آن‌ها برای آموزش مدل‌ها استفاده می‌شود. این مقاله به انواع الگوریتم خوشه بندی پرداخته است.

در مقابل زمانی‌که قصد داریم مدل‌هایی برای حل مشکلات دنیای واقعی آموزش دهیم – اکثر مواقع – از داده‌های بدون برچسب استفاده می‌کنیم. در این حالت باید مدل‌هایی از یادگیری ماشین توسعه دهیم که بتوانند شباهت‌های میان داده‌ها را بیابند و بر اساس این شباهت‌ها داده‌ها را طبقه‌بندی کنند؛ در مراحل بعد از این مدل‌ها برای دسته‌‌بندی داده‌های جدید استفاده می‌شود.

فرایند تحلیل یادگیری بدون نظارت

برای توسعه یک مدل یادگیری بدون نظارت باید مراحل زیر را طی کنیم:

اصلی‌ترین موارد کاربرد یادگیری بدون نظارت عبارتند از:

• تقطیع دیتاست‌ها بر مبنای ویژگی‌های مشترک
• تشخیص ناهنجاری‌هایی که در هیچ گروهی جای نمی‌گیرند
• جمع‌آوری متغیرهایی با ویژگی‌های مشابه و ساده‌سازی دیتاست‌ها

به طور خلاصه هدف یادگیری بدون نظارت مطالعه و بررسی ساختار ذاتی ( و به طور معمول نهفته) داده‌ها است.

به طور کلی یادگیری بدون نظارت در تلاش برای حل دو مشکل عمده است. این دو مشکل عبارتند از:

• خوشه‌بندی
• کاهش ابعاد Dimensionality reduction
  

در مقاله پیش رو به بحث و گفت‌و‌گو راجع به مشکلات خوشه‌بندی خواهیم پرداخت و در مقالات آتی به بررسی مسائل مربوط به کاهش ابعاد می‌پردازیم.

تحلیل خوشه‌بندی

در فرایند خوشه بندی می‌توان اشیای موجود در داده‌ها را به گروه‌های مختلف تقسیم کرد. به منظور گروه‌بندی داده‌ها، الگوریتم خوشه بندی، داده‌ها را بر مبنای ساختار و ویژگی‌های آن‌ها دسته‌بندی می‌کنند، در این حالت اعضای هر خوشه (یا گروه) به یکدیگر بسیار شبیه هستند و با اعضای خوشه‌های دیگر تفاوت‌های بسیاری دارند.

فرض کنید یک دیتاست از فیلم‌ها داریم و قصد داریم آن‌ها را دسته‌بندی کنیم. نقدهایی که از فیلم‌ها در اختیار داریم بدین شرح است:

مدل یادگیری ماشین، بدون نیاز به کسب اطلاعات بیشتر از داده‌ها، می‌تواند تشخیص دهد که دو دسته مختلف وجود دارد.

الگوریتم‌های یادگیری بدون نظارت کاربردهای بی‌شماری دارند و برای حل مشکلات دنیای واقعی از قبیل تشخیص ناهنجاری، سیستم‌های توصیه‌گر، گروه‌بندی اسناد می‌توان استفاده کرد. علاوه بر مواردی که ذکر شد با بهره‌گیری از این الگوریتم‌ها می‌توان مشتریانی که علایق و سلیقه‌های مشابه دارند را بر مبنای خریدهایی که انجام می‌دهند شناسایی کرد.

برخی از محبوب‌ترین انواع الگوریتم خوشه بندی عبارتند از:

• K-Means
• الگوریتم خوشه بندی سلسله مراتبی Hierarchichal clustering
  
• الگوریتم خوشه بندی بر مبنای چگالی Density based scan clustering (DBSCAN)
  
• مدل خوشه‌بندی گوسی Gaussian clustering
  

الگوریتم خوشه بندی K-Means

اجرای الگوریتم‌های K-Means بسیار ساده است و به لحاظ محاسباتی هم بسیار کارآمد هستند و به همین جهت شهرت زیادی کسب کرده‌اند. اما این الگوریتم‌ها در تشخیص دسته‌های موجود در گروه‌هایی که توزیع کروی Spherical distribution شکل ندارند ضعیف عمل می‌کنند.

هدف الگوریتم‌های K-Means یافتن و گروه‌بندی نقطه‌داده‌هایی است که شباهت‌های بسیاری به یکدیگر دارند. منظور از شباهت‌ها فاصله میان نقطه‌داده‌ها است. به عبارت دیگر، هرچه نقطه‌داده‌ها به هم نزدیک‌تر باشند، شباهت بیشتری به یکدیگر دارند و احتمال این‌که در یک خوشه یکسان قرار بگیرند بیشتر است.

مفاهیم کلیدی

• فاصله اقلیدسی مربعی Squared Euclidean Distance
  

فاصله‌ای که بیشترین کاربرد را در الگوریتم k میانگین دارد، فاصله اقلیدسی مربعی است. برای مثال فاصله اقلیدسی میان نقطه  x و نقطه  y در فضای m بُعدی به شرح زیر است:

در اینجا j ، بُعد jام ( یا ستون ویژگی) نمونه نقطه‌های x و y است.

• اینرسی خوشه‌ای Cluster inertia
  

اینرسی خوشه‌ای به مجموع خطاهای مربعی Squared errors  خوشه‌بندی گفته می‌شود و به شرح زیر است:

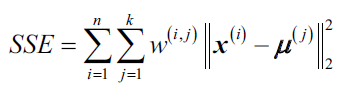
در جایی‌که µ(j) مرکزخوشه Centroid خوشه j باشد و چنان‌چه نمونه x(j) در خوشه j باشد، مقدار w(i,j) برابر با 1  و در غیر این صورت برابر با 0 خواهد بود.

می‌توان گفت الگوریتم خوشه بندی K-Means تلاش می‌کند عامل اینرسی خوشه‌ای را به حداقل برساند.

مراحل الگوریتم

1.  باید k را مشخص کنیم؛ k تعداد خوشه‌هایی است که قصد داریم پیدا کنیم.
2.  الگوریتم مرکز خوشه هر خوشه را به صورت تصادفی انتخاب می‌کند.
3.  الگوریتم هر نقطه‌داده را (با استفاده از فاصله اقلیدسی) به نزدیک‌ترین مرکزخوشه نسبت می‌دهد.
4.  اینرسی خوشه‌ای محاسبه می‌شود.
5.  مرکزخوشه‌های جدید محاسبه می‌شوند؛ عدد به دست آمده میانگین نقطه‌هایی است که متعلق به مرکزخوشه مرحله قبل بوده‌اند . به عبارت دیگر، حداقل خطای متوسط نقطه‌داده‌ها بر مبنای مرکز هر یک از خوشه‌ها محاسبه می‌شود و مرکز را به سمت آن نقطه حرکت می‌دهد.
6. بازگشت به مرحله سوم.

اَبَرپارامترهای K-Means

• Number of clusters: تعداد خوشه‌ها و مرکزخوشه‌هایی که باید تولید شود.
• Maximum iterations: حداکثر تعداد دفعات الگوریتم برای هر اجرا.
• Number initial: تعداد دفعاتی است که الگوریتم با نقاط مختلف مرکزخوشه‌ها اجرا می‌شود. نتیجه نهایی بهترین خروجی تعداد اجراهای متوالی بر حسب اینرسی است.

چالش‌های K-Means

• با توجه به این‌که مرکزخوشه‌های اولیه به صورت تصادفی انتخاب می‌شوند و بر کل فرایند الگوریتم تأثیر می‌گذارند، خروجی تمامی مجموعه‌های آموزشی همیشه یکسان نخواهد بود.
• همان‌گونه که پیش از این نیز گفتیم به خاطر ماهیت فاصله اقلیدسی، این الگوریتم در خوشه‌‌هایی که توزیع کروی شکل ندارند عملکرد مناسبی ندارد.

نکاتی که در هنگام استفاده از K-Means باید به آن‌ها توجه داشته باشید

• برای سنجش ویژگی‌ها باید از یک مقیاس واحد استفاده کرد. به همین دلیل ممکن است لازم باشد استانداردسازی z-score یا مقیاس‌بندی حداقلی – حداکثری را انجام دهیم.
• در مواجهه با داده‌های رسته‌ای Categorical data از تابع get dummies استفاده می‌کنیم.
• تحلیل کاوشگرانه داده‌ها Exploratory Data Analysis (EDA) به شما کمک می‌کند دید کلی از داده‌ها داشته باشید و مشخص کنید که آیا K-Means الگوریتم مناسبی برای شماست یا خیر.
• زمانی‌که با تعداد زیادی ستون سر و کار دارید می‌توانید از روش Minibatch K-Means استفاده کنید، البته باید توجه داشته باشید دقت این روش کمتر است.

انتخاب تعداد k مناسب

در هنگام استفاده از الگوریتم k میانگین ضروری است تعداد خوشه‌هایی که انتخاب کنید مناسب باشد. در ادامه به معرفی چندین روش انتخاب صحیح خوشه می‌پردازیم:

• Field knowledge
• Business decision
• Elbow method

روش elbow با ماهیت علوم داده همخوانی دارد و و برای تصمیم‌گیری داده‌ها را تحلیل می‌کند و به همین‌ دلیل طرفداران بیشتری دارد.

روش Elbow

از روش elbow برای تعیین تعداد صحیح خوشه‌ها در یک دیتاست استفاده می‌شود. در این روش مقادیر افزایشی k  بر روی محور افقی و مجموع خطاهایی که در هنگام استفاده از k میانگین رخ داده بر روی محور عمودی ترسیم می‌شود.

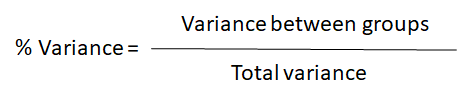
هدف از استفاده از این روش یافتن kای است که برای هر خوشه واریانس را زیاد افزایش ندهد.

در این حالت k=3 که elbow در آنجا قرار گرفته است را انتخاب می‌کنیم.

محدودیت‌های K-Means

هرچند K-Means الگوریتم خوشه بندی بسیار مناسبی است، اما بیشتر مناسب مواقعی است که از قبل تعداد دقیق خوشه‌ها را می‌دانیم و با توزیع‌های کروی شکل سروکار داریم.

تصویر مقابل نشان می‌دهد که اگر تعداد دقیق خوشه‌ها را از قبل بدانیم و از خوشه‌بندی k میانگین استفاده کنیم چه اتفاقی می‌افتد:

به طور معمول از الگوریتم خوشه بندی k میانگین به عنوان معیاری برای ارزیابی عملکرد سایر روش‌های خوشه‌بندی استفاده می‌شود.

خوشه‌بندی سلسله مراتبی

خوشه‌بندی سلسله مراتبی جایگزینی برای انواع الگوریتم خوشه بندی مبتنی بر نمونه‌های اولیه Prototype-based clustering algorithms است. اصلی‌ترین مزیت خوشه‌بندی سلسله مراتبی این است که در این روش نیازی به تعیین تعداد خوشه‌ها نیست، در این روش الگوریتم خوشه بندی تعداد خوشه‌ها را پیدا می‌کند. علاوه بر این خوشه‌بندی سلسله مراتبی امکان ترسیم دندروگرام Dendrogram را فراهم می‌کند. دندروگرام‌ها نشان‌دهنده خوشه‌بندی سلسله مراتبی باینری هستند.

مشاهداتی که در قسمت پایین به هم متصل هستند مشابه یکدیگر هستند و مشاهدات قسمت بالا کاملاً با یکدیگر تفاوت دارند. در دندروگرام‌ها به جای محور افقی بر روی محور افقی نتیجه‌گیری می‌شود.

انواع خوشه‌بندی سلسله مراتبی

خوشه‌بندی سلسله مراتبی به دو نوع تقسیم می‌شود: تجمیعی Aglomerative و تقسیمی Divisive.

تقسیمی: در این روش ابتدا تمامی نقطه‌داده‌ها در یک خوشه واحد جمع می‌شوند. سپس خوشه به طور مداوم به خوشه‌های کوچک‌تر تقسیم می‌شود. این کار تا زمانی‌که هر خوشه تنها شامل یک نمونه باشد ادامه پیدا می‌کند.

تجمیعی: در این روش هر نمونه یک خوشه جداگانه است. سپس این خوشه‌ها با خوشه‌هایی که به آن‌ها نزدیک‌تر هستند ترکیب می‌شوند و این کار تا زمانی‌که یک خوشه واحد تشکیل شود ادامه پیدا می‌کند.

پیوند تکی و پیوند کامل

این الگوریتم که Single linkage (نزدیک‌ترین فاصله) نامیده می‌شود، به همراه پیوند کامل Complete linkage (دورترین فاصله) رایج‌ترین الگوریتم‌های به کاررفته در خوشه‌بندی سلسله مراتبی تجمیعی هستند.

• پیوند تکی

این الگوریتم، یک الگوریتم تجمیعی است. این الگوریتم خوشه بندی هر نقطه نمونه را یک خوشه در نظر می‌گیرد. در مرحله بعد این الگوریتم برای هر جفت خوشه، فاصله میان اعضایی که بیشترین شباهت را به یکدیگر دارند محاسبه می‌کند و دو خوشه‌ای که فاصله اعضای آن‌ها کمتر بوده (اعضایی که بیشترین شباهت را به هم داشته‌اند) را با هم ترکیب می‌کند.

• پیوند کامل

الگوریتم پیوند کامل مشابه الگوریتم خوشه بندی پیوند‌‌‌‌‌‌‌‌‌ ‌‌‌‌‌‌تکی است اما روش کاملاً متفاوتی را دنبال می‌کنند. الگوریتم پیوند کامل نقطه‌داده‌های کاملاً متفاوت دو خوشه را با یکدیگر مقایسه می‌کند و سپس آن‌ها را با هم ترکیب می‌کند.

مزایای خوشه‌بندی سلسله مراتبی

• نمایش‌های حاصل از خوشه‌بندی سلسله مراتبی می‌تواند حاوی اطلاعات مفید و سودمندی باشد.
• دندروگرام‌ها روش جالب و آموزنده‌ای برای مصور‌سازی هستند.
• دندروگرام‌ها به ویژه زمانی‌ سودمند هستند که دیتاست‌ها شامل روابط سلسله مراتبی واقعی باشند.

معایب خوشه‌بندی سلسله مراتبی

• این روش نسبت به داده‌های پرت بسیار حساس هستند و در صورت وجود این‌گونه داده‌ها عملکرد مدل تا حد زیادی کاهش پیدا می‌کند.
• به لحاظ محاسباتی بسیار گران است.

خوشه‌بندی مکانی داده‌های دارای نویز بر مبنای چگالی

خوشه‌بندی مکانی داده‌های دارای نویز بر مبنای چگالی Density-based spatial clustering of applications with noise یا به اختصار DBSCAN یکی دیگر از الگوریتم‌های خوشه‌بندی است که برای تشخیص نویز در داده‌ها از آن استفاده می‌شود.

معیار اختصاص DBSCAN

این روش مبتنی بر تعدادی نقطه با یک شعاع ε مشخص است و هر نقطه‌داده با یک برچسب خاص برچسب‌گذاری می‌شود. فرایند اختصاص برچسب به هر نقطه‌داده به شرح زیر است:

• برچسب تعداد مشخصی (MinPts) از نقاط همسایه است. چنان‌چه این تعداد نقاط MinPts در شعاع ε قرار بگیرند، یک نقطه مرکزی Core point نسبت داده می‌شود.
• نقطه مرزی در ε شعاع نقطه مرکزی قرار خواهد گرفت اما نسبت به تعداد MinPts همسایه‌های کمتری خواهد داشت.
• تمامی نقاط دیگر نقاط نویز Noise point خواهند بود.

الگوریتم DBSCAN

الگوریتم خوشه بندی DBSCAN به روش زیر عمل می‌کند:

• نقاط مرکزی را شناسایی می‌کند و برای هر یک از آن‌ها یا برای هر یک از گروه‌هایِ متصلِ نقاط مرکزی (در صورتی‌که اثبات کنند نقطه مرکزی هستند) یک گروه تشکیل می‌دهد.
• نقاط مرزی Border point را شناسایی می‌کند و به نقاط مرکزی مربوطه نسبت می‌دهد.

در تصویر زیر این فرایند به صورت خلاصه نشان داده شده است:

مقایسه خوشه‌بندی K-Means و DBSCAN

مزایای DBSCAN

• در این روش نیازی به مشخص کردن تعداد خوشه‌ها نیست.
• خوشه‌ها می‌توانند اشکال و اندازه‌های متفاوتی داشته باشند و از این لحاظ بسیار انعطاف‌پذیر هستند.
• این روش برای شناسایی و کار با داده‌های نویز و داده‌ها پرت بسیار مناسب است.

معایب DBSCAN

• در هنگام مواجهه با نقاط مرزی که از دو خوشه قابل دسترس هستند به مشکل می‌خورد.
• در شناسایی خوشه‌هایی با چگالی متفاوت عملکرد مناسبی ندارد.

مدل‌های مخلوط گوسی

مدل‌های مخلوط گوسی Gaussian Mixture Models (GMM) به مدل‌های احتمالی گفته می‌شود که تصور می‌کنند تمامی نمونه‌ها از ترکیب تعداد کمی توزیع گوسی با پارامترهای نامشخص ایجاد شده‌اند.

این مدل‌ها در دسته انواع الگوریتم خوشه بندی نرم Soft clustering قرار می‌گیرند؛ در این گروه از الگوریتم‌ها هر نقطه‌داده به یک خوشه در دیتاست تعلق می‌گیرد اما سطح عضویت آن‌ها در هر خوشه متفاوت است. منظور از عضویت احتمال تعلق داشتن به یک خوشه خاص است و در بازه 0 تا  1 قرار می‌گیرد.

برای مثال نقاطی که هایلات شده‌اند همزمان به خوشه A و B تعلق دارند اما به دلیل این‌که به گروه A نزدیک‌تر هستند بیشتر در این گروه قرار می‌گیرند.

GMM یکی از پیشرفته‌ترین روش‌های خوشه‌بندی‌ است. در این روش فرض بر این است که هر خوشه یک توزیع احتمالی را دنبال می‌کند؛ این توزیع می‌تواند گوسی یا نرمال باشد. GMM تعمیمی از خوشه‌بندی k میانگین است و شامل اطلاعاتی راجع به ساختار کوواریانس داده‌ها و هم‌چنین مراکز گوسی‌های نهفته Latent Gaussians است.

توزیع GMM در یک بعد

GMM توزیع‌های گوسی را در دیتاست جست‌و‌جو می‌کند و آن‌ها را با هم ترکیب می‌کند.

GMM در دو بعد

هر زمان‌که توزیع‌هایی چندمتغیره Multivariate distribution همانند توزیع مقابل داشته باشیم مرکزخوشه هر یک از محورهای توزیع دیتاست µ + σ خواهد بود.

الگوریتم GMM

الگوریتم GMM یک الگوریتم بیشینه‌سازی انتظار Expectation maximization algorithm است و فرایند آن به شرح زیر است:

1. توزیع‌های گوسی k را تعریف می‌کند. این الگوریتم برای تعریف توزیع‌‌های گوسی از مقادیر µ (میانگین) و σ ( انحراف از معیار) استفاده می‌کند. میانگین و انحراف از معیار را می‌توان از دیتاست (ساده‌ترین روش) و یا با اعمال k میانگین به دست آورد.
2. خوشه‌بندی نرم داده‌ها: این مرحله، مرحله «انتظارات» است که در آن تمامی نقطه‌داده‌ها با سطح عضویت مربوطه خود به یک خوشه‌ نسبت داده می‌شوند.
3. تخمین مجدد گوسی‌ها: این مرحله، مرحله «بیشینه‌سازی» است که در آن انتظارات بررسی می‌شوند و از آن‌ها برای محاسبه پارامترهای جدید برای گوسی‌ها استفاده می‌شود: µ و σ جدید.
4. به منظور بررسی همگرایی، لگاریتم شباهت Log-likelihood داده‌ها را ارزیابی می‌کند. هر چه لگاریتم شباهت بیشتر باشد احتمال این‌که ترکیب ایجادشده از مدل‌ها مناسب دیتاست باشد بیشتر است. بنابراین این یک تابع بیشینه‌سازی است.
5. تا رسیدن به همگرایی از مرحله 2 به بعد را تکرار می‌کند.

مزایای GMM

• GMM یک روش خوشه‌بندی نرم است که نقاط نمونه را به چندین خوشه نسبت می‌دهد. این ویژگی موجب شده الگوریتم GMM به سریع‌ترین الگوریتم در یادگیری مدل‌های مخلوط تبدیل شود.
• در این روش خوشه‌ها به لحاظ تعداد و اشکال متفاوت و انعطاف‌پذیر هستند.

معایب GMM

• الگوریتم GMM نسبت به مقادیر اولیه بسیار حساس است و این مقادیر می‌تواند کیفیت عملکرد آن را تحت تأثیر قرار دهند.
• GMM ممکن است با کمینه محلی همگرا شود و همین امر باعث می‌شود این الگوریتم کمتر بهینه باشد.
• زمانی‌که به ازای هر مخلوط نقطه‌ کافی وجود نداشته باشد، الگوریتم واگرا می‌شود و راهکارهایی با احتمال درستنمایی‌های بی‌نهایت پیدا می‌کند، مگر این‌که کوواریانس میان داده‌ها را به صورت مصنوعی تنظیم کنیم.

اعتبارسنجی خوشه‌بندی

اعتبارسنجی خوشه‌بندی به فرایند ارزیابی کمی و عینی نتایج یک خوشه گفته می‌شود. برای اعتبارسنجی خوشه‌بندی از شاخص‌های اعتبارسنجی استفاده می‌کنیم. شاخص‌های اعتبارسنجی به سه دسته اصلی تقسیم می‌شوند:

شاخص‌های خارجی

زمانی از شاخص‌های خارجی برای امتیازدهی استفاده می‌کنیم که داده‌های اصلی برچسب‌گذاری شده باشند که در این‌گونه مسائل زیاد رایج نیست. ساختار خوشه‌بندی را با اطلاعاتی که از قبل مشخص شده‌اند مطابقت می‌دهیم.

شاخص رند تعدیل یافته

این شاخص Adjusted rand index (ARI) بیش از سایر شاخص‌ها مورد استفاده قرار می‌گیرد.

• شاخص رند تعدیل یافته € [-1,1]

برای درک این شاخص ابتدا باید مؤلفه‌های آن را تعریف کنیم:

• a: تعداد نقاطی است که در یک خوشه واحد در C و هم‌چنین K قرار دارند.
• B: تعداد نقاطی است که در خوشه‌ای متفاوت در C و هم‌چنین در K قرار دارند.
• n: تعداد کل نمونه‌ها است.

مقدار ARI می‌تواند از -1 تا 1  باشد. هرچه مقدار ARI بیشتر باشد مطابقت بیشتری با داده‌های اصلی خواهد داشت.

شاخص‌های اعتبارسنجی درونی

در یادگیری بدون نظارت با داده‌های بدون برچسب کار می‌کنیم و استفاده از شاخص‌های درونی در این نوع یادگیری بسیار مفید خواهد بود.

یکی از رایج‌ترین شاخص‌های درونی، ضریب نیمرخ Silhouette coefficient است.

• ضریب نیمرخ

برای هر نقطه‌داده یک ضریب نیمرخ وجود دارد.

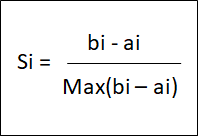
• a: متوسط فاصله تا نمونه‌های بعدی i در همان خوشه است.
• b: متوسط فاصله تا نمونه‌های بعدی i در نزدیک‌ترین خوشه همسایه است.

مقدار ضریب نیمرخ می‌تواند از -1 تا 1 باشد. هرچه مقدار آن بیشتر باشد k‌ای که انتخاب‌ کرده‌ایم بهتر خواهد بود. در صورتی‌که k از حد ایده‌آل بیشتر باشد، ضریب نیمرخ منفی‌تر می‌شود.

این شاخص مناسب الگوریتم‌های به خصوصی از قبیل الگوریتم خوشه بندی k میانگین و الگوریتم خوشه بندی سلسله مراتبی است و در DBSCAN عملکرد مناسبی ندارد و در این نوع خوشه‌بندی از DBCV استفاده خواهیم کرد.