راهنمای استراتژی‌های تکاملی

تیم تحریریه
۳۱ شهریور ۱۴۰۰

زمان مطالعه: 12 دقیقه

در مقاله حاضر، می‌خواهیم چگونگی کارکرد استراتژی‌های تکاملی evolution strategies (ES) را به کمک چند نمونه بصری توضیح دهیم. در این مقاله چگونگی به‌کارگیری الگوریتم‌ها برای انجام کارهای مختلف را شرح خواهیم داد.

مقدمه

مدل‌های شبکه عصبی از انعطاف‌پذیری بالایی برخوردارند. اگر بتوانیم مجموعه مناسبی از پارامترهای مدل را پیدا کنیم، امکان استفاده از شبکه‌های عصبی برای حل بسیاری از مسائل چالش‌برانگیز وجود خواهد داشت.

یادگیری عمیق موفقیتِ خود را تا حد زیادی مرهونِ استفاده از الگوریتم پس‌انتشار (Back-propagation) است که می‌تواند گرادیان تابع هدف را نسبت به هر یک از پارامترهای مدل به شکل کارآمدی محاسبه کند. به کمک این گرادیان‌ها می‌توانیم فضای پارامتر را به شکلی کارآمد جستجو کنیم. همچنین می‌توانیم به راه حل مناسبی برای انجام کارهای سخت، توسط شبکه‌های عصبی دست پیدا کنیم.

با این حال، مسائل بسیاری هم وجود دارند که برای حل آن‌ها نمی‌توان از الگوریتم پس‌انتشار استفاده کرد. برای مثال، در مسائل می‌توان یک شبکه عصبی را آموزش داد به طوری که بتواند یک توالی از حرکت‌ها را برای انجام برخی از وظایف در یک محیط تشکیل دهد.

اما تخمین گرادیان سیگنال‌های پاداش با توجه به حالت عامل در آینده جهت تعیین حرکت کنونی کار ساده‌ای نیست. به ویژه زمانی که پاداش ناشی از حرکت کنونی در آینده تعیین می‌شود. حتی در صورتی که قادر به محاسبه گرادیان‌های دقیق باشیم، مسئلۀ گیر افتادن در بهینه محلی local optimum کماکان وجود دارد.

استراتژی های تکاملی — گیرافتادن در بهینه محلی

در RL یک بخش کامل برای مطالعه مسئله تخصیص اعتبار credit-assignment در نظر گرفته شده و پیشرفت قابل توجهی در سال‌های اخیر در این حوزه به دست آمده است. با این حال، همچنان کار دشواری است؛ به ویژه وقتی که سیگنال‌های پاداش پراکنده باشند.

در دنیای حقیقی، پاداش‌ها می‌توانند پراکنده و نویزدار باشند. گاهی اوقات فقط یک پاداش داریم. بسته به کارفرمایی که داریم، شاید دانستن این که چرا پاداش اینقدر کم است، سخت باشد. پس در مسائلی از این دست نباید به تخمین بی‌معنی گرادیان آینده تکیه کنیم. همچنین نباید سیاست‌های خود را پیرامون آن بچینیم. می‌توانیم استفاده از روش‌های بهینه‌سازی جعبه سیاه (Black Box) مثل الگوریتم‌های ژنتیک یا استراتژی‌های تکاملی را در دستور کارمان قرار دهیم.

در همین راستا، «Open AI» مقاله‌ای با عنوان «استراتژی‌های تکاملی، یک روش جایگزین مقیاس‌پذیر برای یادگیری تقویتی» منتشر کرد. در آن نشان می‌داد استراتژی‌های تکاملی کارآیی کمتری به لحاظ داده‌ای از RL دارند. اما از مزایای بسیاری برخوردارند.

کنار گذاشتنِ محاسبات گرادیان فرصتی به این نوع الگوریتم‌ها می‌دهد تا به شکل موثرتری تکامل یابند. می‌توان محاسابات یک الگوریتم ES را بر روی هزاران ماشین جهت دستیابی به پردازش موازی به اشتراک گذاشت. همچنین با اجرا کردن متعدد این الگوریتم‌ها از ابتدا، می‌توان به سیاست‌های متنوع‌تری در مقایسه با سیاست‌های کشف شده توسط RL دست یافت.

در مسئلۀ شناسایی مدل یادگیری ماشین، مثل طراحی معماری شبکه عصبی، نمی‌توان گرادیان را به‌طور مستقیم محاسبه کرد. اگرچه می‌توان از RL، استراتژی‌های تکاملی، الگوریتم ژنتیک و… برای جستجو در فضای معماری مدل استفاده کرد. اما در مقاله حاضر تمرکز روی استفاده از این الگوریتم‌ها برای جستجوی پارامترهای مدلِ از پیش‌تعریف شده معطوف شده است.

[irp posts=”17100″]

فهرست مقاله پنهان

1 استراتژی‌های تکاملی چه هستند؟

2 استراتژی تکاملی ساده

3 الگوریتم ژنتیک ساده

4 استراتژی‌های تکاملی و سازگاری ماتریس کوواریانس(CMA-ES)

5 استراتژی‌های تکاملی عصبی

6 استراتژی تکاملی Open AI

7 شکل دهی برازش

8 MNIST

9 خودتان امتحان کنید

استراتژی‌های تکاملی چه هستند؟

تابع Rastrigin تعداد زیادی بهینه محلی دارد

پیش از توضیح استراتژی‌های تکاملی به دو نمودار زیر توجه کنید. نمودارهای زیر توابع دوبعدی Schaffer(شکل سمت چپ) و Rastrigin(شکل سمت راست) را نشان می‌دهند. دو مسئله ساده که برای آزمایش الگوریتم‌های بهینه‌سازی جعبه سیاه پیوسته مورد استفاده قرار می‌گیرند. بخش‌های روشن‌تر نمودار مقادیر بیشتر توابع F(x, y) را نشان می‌دهند.

همان‌طور که در این نمودار مشاهده می‌کنید، بهینه‌های محلی زیادی در این تابع وجود دارد. ما باید یک مجموعه پارامتر مدل
(x,y) پیدا کنیم؛ طوری که (F(x, y بیشترین نزدیکی را به حداکثر سراسری global maximum داشته باشد. تعاریف متعددی از استراتژی‌های تکاملی ارائه شده است. اما می‌توان استراتژی‌های تکاملی را به عنوان الگوریتمی تعریف کرد که مجموعه‌ای از راه‌حل‌های احتمالی را در اختیار کاربر قرار می‌‌دهد تا بتواند مسئله‌ای را ارزیابی کند.

فرایند ارزیابی بر پایه تابع هدف است که راه حل معینی را می‌گیرد و یک مقدار برازش ارائه می‌کند. بر اساس نتایج برازشِ راه‌حل‌های موجود، الگوریتم به تولید نسل بعدیِ راه‌حل‌های نامزد خواهد پرداخت. انتظار می‌رود نتایج بهتری در مقایسه با نسل فعلی حاصل شود.

فرایند تکراری زمانی متوقف می‌شود که کاربر به بهترین راه‌حل ممکن دست پیدا کند. با توجه به یکی از الگوریتم‌های استراتژی‌های تکاملی موسوم به EvolutionStrategy، می‌توان به شیوه زیر اقدام کرد:

solver = EvolutionStrategy()
while True:

# ask the ES to give us a set of candidate solutions
solutions = solver.ask()

# create an array to hold the fitness results.
fitness_list = np.zeros(solver.popsize)

# evaluate the fitness for each given solution.
for i in range(solver.popsize):
fitness_list[i] = evaluate(solutions[i])

# give list of fitness results back to ES
solver.tell(fitness_list)

# get best parameter, fitness from ES
best_solution, best_fitness = solver.result()

if best_fitness > MY_REQUIRED_FITNESS:
   break

اگرچه اندازه جمعیت در هر نسل ثابت نگه داشته می‌شود، اما نیازی به این کار نیست. استراتژی تکاملی می‌تواند هر تعداد راه‌حل احتمالی که می‌خواهد ایجاد کند. زیرا راه‌حل‌های ایجاد شده توسط استراتژی‌های تکاملی در توزیعی نمونه‌گیری می‌شوند که پارامترهای آن در هر نسل، به واسطه استراتژی‌های تکاملی به‌روزرسانی می‌شوند. این فرایند نمونه‌گیری را با مثالی از استراتژی تکاملی ساده توضیح می‌دهیم.

استراتژی تکاملی ساده

در یکی از ساده‌ترین استراتژی‌های تکاملی، مجموعه راه‌حل‌ها از توزیع نرمال نمونه‌گیری می‌شوند؛ با میانگینμ و انحراف معیار ثابت σ. در مسئله دوبعدی داریم: μ=(μx,μy) و σ=(σx,σy). در ابتدا، μ بوسیله مرکز فضای مسئله مقداردهی می‌شود. پس از اینکه نتایج برازش مورد ارزیابی قرار گرفت، باید μ را به بهترین راه‌حل در جمعیت جواب‌ها مقداردهی شود.

نسل بعدی راه‌حل‌ها باید بر اساس میانگین جدید نمونه‌گیری شوند. این نحوه عملکرد الگوریتم در 20 نسل است که در دو مسئله فوق به کار گرفته شده است.

نمودار بالا، نقطه سبز نشان‌دهنده میانگین توزیع در هر نسل است. نقاط آبی به راه‌حل‌های نمونه‌گیری شده اشاره می‌کنند و نقطه قرمز بهترین راه‌حلی است که تاکنون الگوریتم موفق به یافتنِ آن شده است. این الگوریتم ساده تنها برای مسائل ساده کارساز است.

با توجه به ماهیت حریصی که این الگوریتم دارد، فقط بهترین راه‌حل را حفظ می‌کند. ممکن است در مسائل پیچیده‌تر به مشکل برخورده و در بهینه محلی گیر بیفتد. بهتر است نسل بعدی را از توزیعی احتمالی نمونه‌گیری کند. توزیعی که مجموعه متنوعی از ایده‌ها را ارائه کرده باشد؛ نه اینکه به بهترین راه‌حل از نسل فعلی اکتفا کند.

الگوریتم ژنتیک ساده

الگوریتم ژنتیک genetic algorithm یکی از قدیمی‌ترین الگوریتم‌های بهینه‌سازی شمرده می‌شود که انواع مختلفی دارد و هر کدام از آن‌ها در سطح متفاوتی پیچیده هستند، اما در این مقاله ساده‌ترین نسخه معرفی می‌شود.

این ایده ساده را در نظر بگیرید: تنها 10 درصد از بهترین راه‌حل‌ها را در نسل فعلی نگه دارید و بگذارید بقیه جمعیت از بین بروند. در نسل بعدی، برای نمونه‌گیریِ راه‌حل جدید، باید دو راه‌حل را به صورت تصادفی از بازماندگان نسل قبلی انتخاب کنید و با ادغام مجدد پارامترهایشان به ایجاد یک راه‌حل جدید برسید.

در این فرایندِ نوترکیب (crossover)، از روش پرتاب سکه برای تعیین هر پارامتر از والدها استفاده می‌شود. در تابع دو بعدی مثال قبل، هر یک از جواب‌های جدید ممکن است x یا y را به احتمال 50 درصد از هر یک از والدین به ارث ببرند. پس از این فرایند نوترکیب نویز گاوسی Gaussian noise با انحراف معیار ثابت، به هر راه‌حل جدید اضافه می‌شود.

شکل فوق چگونگی کارکرد الگوریتم ژنتیک ساده را نشان می‌دهد. نقاط سبز اعضای جمعیت منتخب از نسل قبلی را نشان می‌دهند. نقاط آبی فرزندانی هستند که مجموعه راه‌حل‌های احتمالی را ایجاد می‌کنند. نقطه قرمز هم نشانگرِ بهترین راه‌حل است.

الگوریتم‌های ژنتیک با شناسایی مجموعه متنوعی از راه‌حل‌های احتمالی به منظور تکثیر نسل بعدی نقش مهمی در تنوع ایفا می‌کنند. با این حال، با گذشت زمان اکثر راه‌حل‌ها در جمعیت منتخبِ بازمانده به سمت بهینه محلی همگرا می‌شوند.

نسخه‌های پیچیده‌تری از الگوریتم‌های ژنتیک هم وجود دارند که از جمله آن‌ها می‌توان به CoSyNe، ESP و NEAT اشاره کرد. در این الگوریتم‌ها، راه‌حل‌های مشابه در جمعیت، با گونه‌های مختلف خوشه‌بندی می‌شوند تا از تنوع و گوناگونی در طی زمان اطمینان حاصل شود.

استراتژی‌های تکاملی و سازگاری ماتریس کوواریانس(CMA-ES)

یکی از معایب الگوریتم‌های ژنتیک ساده و استراتژی‌های تکاملی ساده این است که پارامتر نویز، انحراف معیار ثابتی دارد. گاهی اوقات می‌خواهیم کاوش بیشتری انجام داده و انحراف معیار فضای جستجویمان را افزایش دهیم.

گاهی اوقات هم به سطحی کافی از اطمینان رسیده‌ایم و می‌دانیم که جواب بهینه نزدیک است. بنابراین فقط باید به تنظیم دقیق جواب بپردازیم. ما می‌خواهیم فرایند جستجو به شکل زیر انجام شود:

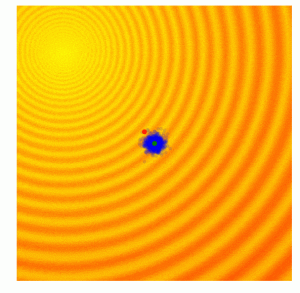
این همان چیزی است که به دنبالش بودیم. فضای جستجویِ نشان داده شده در شکل فوق با استراتژی تکاملیِ «CMA-ES» ساخته شده است. «CMA-ES» الگوریتمی است که می‌تواند نتایج هر نسل را ثبت کند. می‌تواند به شکلی مناسب به افزایش یا کاهش فضای جستجو در نسل بعدی بپردازد.

[irp posts=”17100″]

این الگوریتم نه تنها خود را برای میانگین μ و پارامترهای سیگما را سازگار می‌کند، بلکه می‌تواند ماتریس کوواریانس کامل فضای پارامتر را محاسبه کند. در هر نسل، «CMA-ES» پارامترهای یک توزیع نرمال چندمتغیره multi-variate normal distribution را برای نمونه‌گیری از راه‌حل‌ها فراهم می‌کند. بنابراین، این الگوریتم از کجا می‌داند که فضای جستجو را چگونه افزایش یا کاهش دهد؟

قبل از بحث درباره روش کارکرد آن، بگذارید چگونگی تخمین ماتریس کوواریانس را با هم مرور کنیم، چرا که برای درک روش «CMA-ES» در بخش‌های بعدی اهمیت زیادی دارد. اگر بخواهیم ماتریس کوواریانس کل جمعیت نمونه‌گیری شده را تخمین بزنیم، می‌توانیم از مجموعه معادلات زیر استفاده کنیم.

از این معادله‌ها می‌توان برای محاسبه تخمین درست نمایی بیشینه از یک ماتریس کوواریانس نیز استفاده کرد. در ابتدا باید میانگین هر کدام از x_iو y_iرا محاسبه کرد.

عبارات ماتریس کوواریانس 2×2 به صورت زیر خواهد بود:

البته این مقادیر میانگین تخمین زده شده u_x و u_y و عبارات کوواریانس σ_x_،σ_y_،σ_xy فقط برآوردی از ماتریس کوواریانس حقیقی هستند و لزوماً برای ما فایده‌ای ندارند. «CMA-ES» فرمول محاسبه کوواریانسِ بالا را به شیوه‌ای شفاف اصلاح می‌کند تا آن را با مسئله بهینه‌سازی سازگار کند.

چگونگی انجام گام به گام این فرایند را توضیح می‌دهیم. در ابتدا، «CMA-ES» روی Nbest عدد از بهترین راه‌حل‌ها در نسل فعلی تمرکز می‌کند. برای سهولت کار، بگذارید فرض کنیم Nbest برابر با ۲۵ درصد از تعداد راه‌حل‌ها باشد. پس از مرتبط‌سازی راه‌حل‌ها پس از مرتبط‌سازی راه‌حل‌ها بر اساس میزان ارزیابی‌شان، میانگین میانگین u^(g+1) نسل بعدی (g+1) براساس 25 درصد از بهترین جواب‌های نسل فعلی مورد محاسبه قرار می‌گیرد. بنابراین فرایند مذکور به صورت زیر انجام می‌شود:

در گام بعدی، فقط از 25 درصد راه‌حل برتر برای تخمین ماتریس کوواریانس C^(g+1) نسل بعدی استفاده می‌شود، اما u^(g+1) نسل فعلی هم به جای پارامترهای به‌روزرسانی شده u^(g+1) که قبلاً محاسبه کرده بودیم، مورد استفاده قرار می‌گیرد:

با برخورداری از مجموعه σ_x_،σ_y، u_y ،u_x و σ_xy پارامترها برای نسل بعدی (g+1)، امکان نمونه‌گیری از نسل بعدیِ راه‌حل‌های احتمالی فراهم میشود.

در زیر، مجموعه‌ای از اَشکال را آورده‌ایم که چگونگیِ استفاده از نتایج نسل فعلی (g) را برای تولید راه‌حل در نسل بعدی(g+1) نشان می‌دهد:

1. امتیاز برازش هر راه‌حل احتمالی در نسل (g) را محاسبه کنید.
2. آن 25 درصد راه‌حل برتر در جمعیت نسل (g) را جدا کنید (به رنگ بنفش).
3. با استفاده از بهترین راه‌حل‌ها و میانگین u^(g) نسل فعلی (نقطه سبز)، ماتریس کوواریانس C^(g+1) نسل بعدی را محاسبه کنید.
4. مجموعه جدیدی از راه‌حل‌های احتمالی را با استفاده از میانگین به‌روزرسانی شده u^(g+1) و ماتریس کوواریانس C^(g+1)نمونه‌گیری کنید.
بیایید یک بار دیگر جزئیات این مسئله را در کل فرایندِ جستجو بررسی کنیم:

از آنجایی که «CMA-ES» می‌تواند میانگین و ماتریس کوواریانس را با استفاده از اطلاعات حاصل از بهترین راه‌حل‌ها تنظیم و هماهنگ کند، وقتی که راه‌حل‌ها فاصله زیادی با هم داشته باشند، می‌تواند شبکه وسیع‌تری را در بر گیرد؛ یا حتی وقتی بهترین راه‌حل‌ها فاصله نزدیکی با هم دارند، فضای جستجو را تنگ‌تر کند.

در این مقاله سعی شده الگوریتم «CMA-ES» را تا حد زیادی ساده‌سازی کنیم. این الگوریتم یکی از متداول‌ترین و مشهورترین الگوریتم‌های بهینه‌سازی به حساب می‌آید که محققان زیادی آن را برای انجام کارهای تحقیقاتی خود انتخاب می‌کنند. تنها عیب الگوریتم «CMA-ES» این است که اگر تعداد پارامترهای مدل خیلی زیاد باشد، عملکردش دچار اختلال می‌شود. وقتی فضای جستجو کمتر از ده هزار پارامتر باشد، به نظر الگوریتم «CMA-ES» انتخاب مناسبی است؛ در صورتی که ما به اندازه کافی صبور باشیم.

[irp posts=”17100″]

استراتژی‌های تکاملی عصبی

فرض کنید یک شبیه‌ساز زندگی مصنوعی ساخته‌اید. همچنین از یک شبکه عصبی متفاوت نمونه‌گیری می‌کنید تا رفتار هر مورچه در کلونی مورچه‌ها را کنترل کنید. استفاده از استراتژی‌های تکاملی ساده برای این کار، می‌تواند خصوصیات و رفتارهایی را بهینه‌سازی کند که به نفع تک‌تک مورچه‌ها خواهد بود.

در هر نسل متوالی جمعیت پر از مورچه‌های آلفایی خواهد بود که تنها به سلامت خود اهمیت می‌دهند. به جای استفاده از قانونی که بر اساس بقای بهترین مورچه‎ هاست، چه می‌شود اگر روش جایگزین دیگری را در پیش گیرید. همچنین مجموع کلیه مقادیر برازش جمعیت مورچه‌ها را بهینه‌سازی کنید. هدف از این کار، اطمینان داشتن از سلامت کل جمعیت مورچه‌ها در نسل‌های متوالی است.

یکی از نقاط ضعف الگوریتم‌های بررسی شده تا به اینجا، این است که اکثر راه‌حل‌ها را کنار می‌گذارند. آن‌ها فقط بهترین راه‌حل‌ها را نگه می‌دارند. راه‌حل‌های ضعیف حاوی اطلاعاتی درباره مواردی هستند که نباید آن‌ها را انجام داد. از این نوع اطلاعات می‌توان به شکل بهتری برای برآورد نسل بعدی استفاده کرد.

مقاله ای در سال 1992 میلادی منتشر شد. در آن ویلیام از روشی برای تخمین گرادیان پاداش‌های مورد انتظار در رابطه با پارامترهای مدل یک شبکه عصبی سخن گفته بود.

در این مقاله، استفاده از «REINFORCE» در بخش ششم مقاله به عنوان یکی از استراتژی‌های تکاملی پیشنهاد شد. مورد ویژۀ «REINFORCE-ES» در بخش‌های بعدی مقاله هم مورد بحث و بررسی قرار گرفت. در این روش می‌خواهیم از کلیه اطلاعاتِ مربوط به هر یک از اعضای جمعیت (خوب یا بد) استفاده کنیم تا سیگنال گرادیان را تخمین بزنیم؛ سیگنالی که می‌تواند کل جمعیت را به جهت بهتری در نسل بعدی هدایت کند.

از آنجا که تخمینِ گرادیان در دستور کار ما قرار دارد، می‌توانیم از این گرادیان در قانون به‌روزرسانی استاندارد گرادیان کاهشی تصادفی(SGD) Stochastic Gradient Descent (SGD) برای یادگیری عمیق استفاده کنیم. امکان استفاده از این گرادیان تخمینی با «Momentum SGD»، «RMSProp» یا «Adam» نیز وجود دارد. هدف این است که امتیاز مورد انتظارِ برازش در راه‌حل‌های نمونه‌گیری شده افزایش پیدا کند.

اگر نتیجه به اندازه کافی خوب باشد، در این صورت بهترینِ عضوِ جمعیت حتی عملکرد بهتری از خود بر جای خواهد گذاشت. بنابراین، بهینه‌سازی در این مورد روش معقولی است. افزایش امتیاز مورد انتظارِ برازش در راه‌حل نمونه‌گیری شده به این کار شبیه است که امتیاز برازش کل جمعیت را افزایش دهیم.

اگر z یک بردار راه‌حل باشد که از تابع توزیع احتمال π(z,θ) نمونه‌گیری شده است، می‌توان مقدار مورد انتظار تابع هدف F را به ترتیب زیر تعریف کرد:

که در آن θ پارامترهای تابع توزیع احتمال هستند. برای مثال، اگر π را یک توزیع نرمال در نظر بگیریم، در این صورت θعبارت است از μو σ. در مسائل دو بعدی ساده که پیش ازاین مطرح کردیم، هر z یک بردار دوبعدی (x, y) است.

مقاله «NES» مشتق خوبی از گرادیان J(θ) نسبت به θ ارائه می‌کند. استفاده از روش log-likelihood مانند آنچه که در الگوریتم REINFORCE ارائه شده، به ما اجازه می‌دهد که گرادیان J(θ) را به صورت زیر محاسبه کنیم:

در اندازه جمعیت N، که راه‌حل‌های z^N ….. z³ ،z² ، z¹ را در اختیار داریم، می‌توانیم این گرادیان را بصورت زیر تخمین بزنیم:

با این گرادیان، می‌توان از پارامتر میزان یادگیری α استفاده کرد و شروع به بهینه‌سازی پارامترهای θدر π کرد؛ به طوری که راه‌حل‌های نمونه‌گیری شده به امتیاز بالایی در تابع هدف F می‌رسند. با استفاده از SGD (یا Adam) هم می‌توان θ را برای نسل بعدی به‌روزرسانی کرد:

سپس مجموعه جدیدی از راه‌حل‌های نامزد z را از این pdf به‌روزرسانی شده نمونه‌گیری کرده و تا جایی ادامه دهیم که راه‌حل رضایت‌بخش بدست آید. در بخش 6 از مقاله «REINFORCE»، ویلیامز فرمول‌های فرم بسته ∇_θ logπ(zⁱ,θ) برای مورد ویژه ای که در آن π(z, θ) یک توزیع نرمال چند متغیره فاکتورشده است، را مورد محاسبه قرار داده است.

در این مورد خاص θ عبارت است از بردارهای μو σ. بنابراین، هر عنصر راه‌حل را می‌توان از توزیع نرمال تک‌متغیری Z_j_~N(u_j, σ_j) نمونه‌گیری کرد. فرمول‌های فرم بستۀ مربوط به ∇_θ logπ(zⁱ,θ) برای هر عنصر از بردار θدر هر راه‌حل در جمعیت جواب‌ها به صورت زیر محاسبه می‌شود:

برای شفافیت در کار می‌توان از شاخص j برای شمارش در فضای پارامتر استفاده کرد و نباید این را با اندیس ii اشتباه گرفت که برای شمارش اعضای نمونه‌گیری شده در جمعیت به کار برده می‌شود. در مسائل دوبعدی، شرایط زیر حاکم است:

Z_{1 =}x_,z_{2 =}y , μ_{1 =}μ_x، μ_{2 =}μ_y_،σ₁₌σ_x_،σ₂₌σ_y

این دو فرمول را می‌توان در فرمول گرادیان تقریبی جایگذاری کرد تا قوانین به‌روزرسانیِ صریح μو σ بدست آید. در مقاله‌هایی که در بخش‌های قبلی اشاره شد، قوانین به‌روزرسانی صریح‌تری بدست آمد و ترفندهای دیگری هم معرفی شد، مثل نمونه‌گیری متضاد در PEPG که روش ما هم مبتنی بر آن است.

در مقاله «NES»، استفاده از معکوسِ ماتریس اطلاعات Fisher در قانون به‌روزرسانیِ گرادیان مد نظر قرار گرفت. اما مفهوم کلی اساساً با سایر الگوریتم‌های استراتژی‌های تکاملی یکسان است. یعنی میانگین و انحراف معیار توزیع نرمال چندمتغیری در هر نسل جدید به‌روزرسانی می‌شود و مجموعه جدیدی از راه‌حل‌ها با توزیع به‌روزرسانی شده انتخاب می‌شوند. در زیر تصویری از این الگوریتم به نمایش درآمده است. فرمول‌های توضیح داده شده در بخش‌های قبلی هم در اینجا به کار برده شده است:

همان طور که می‌بینید این الگوریتم می‌تواند به‌صورت پویا σ را برای جستجو یا تنظیم فضای راه‌حل تغییر دهد. برخلاف CMA-ES، هیچ ساختار همبستگی در روش انجامِ ما وجود ندارد؛ بنابراین، توجهِ ما فقط روی نمونه‌های افقی یا عمودی است. هرچند در صورت نیاز می‌توانیم قوانین به‌روزرسانی را برای کل ماتریس کوواریانس به کار ببریم.

این الگوریتم از دید ما الگوریتم خوب و کارآمدی است؛ زیرا σ می‌تواند وفق پیدا کند، بنابراین فضای جستجوی ما می‌تواند در طول زمان توسعه یابد یا محدود شود. چون پارامتر همبستگی در این روش استفاده نمی‌شود، بازده الگوریتم برابر است با O(N). پس اگر عملکرد CMA-ES به مشکل بخورد، می‌توان از PEPG استفاده کرد. معمولاً زمانی از PEPG استفاده می‌کنیم که تعداد پارامترهای مدل از چند هزار تخطی کرده باشد.

استراتژی تکاملی Open AI

در مقاله «OpenAI»، از یک استراتژی تکاملی که مورد خاصی از الگوریتم «REINFORCE-ES» است، استفاده می‌شود. این الگوریتم در بخش‌های قبلی توضیح داده شد. در عمل σ ثابت در نظر گرفته شده است، و فقط پارامتر u در هر نسل بروز رسانی می‌شود. در شکل زیر، چگونگی کارکرد این استراتژی نشان داده‌ شده است بطوری که پارامتر σ ثابت می‌باشد.

این مقاله علاوه بر ساده‌سازی مراحل کار، قانون به‌روزرسانی را هم اصلاح کرده است. در نتیجه می‌تواند برای پردازش موازی در ماشین‌های مختلف استفاده شود. بر اساس قانون به‌روزرسانیِ آن‌ها، طیف وسیعی از اعداد تصادفی با استفاده از یک مقدار ثابت از پیش محاسبه شده‌اند.

با انجام این کار، هر عامل می‌تواند پارامترهای عوامل دیگر را در طول زمان تکثیر کند. می‌تواند هر عامل تنها نیاز دارد یک عدد که همان نتیجه تابع ارزیابی نهایی است را با سایر عامل‌ها به اشتراک بگذارد. این کار زمانی اهمیت پیدا می‌کند که بخواهیم استراتژی‌های تکاملی را برای هزاران یا میلیون‌ها عامل که در ماشین‌های مختلف واقع شده‌اند، به کار ببریم.

شاید مقدور نباشد در هر به‌روزسانی نسل، کل بردار راه‌حل را یک میلیون بار منتقل کنیم. پس بهتر است فقط به انتقال نتایج برازش نهایی بسنده کنیم. محققان در مقاله خود نشان داده‌اند که با استفاده از 1440 عامل در Amazon EC2 می‌توانند مسئله راه رفتن Mujoco Humanoid را تقریباً در ده دقیقه حل کنند.

از نظر ما، قانون به‌روزرسانی موازی باید در الگوریتم اصلی به خوبی عمل کند. چرا که امکان به‌کارگیری σ نیز وجود دارد. اما شاید در عمل بخواهیم در آزمایش‌های محاسبات موازی بزرگ‌مقیاس، تعداد را کاهش دهیم.

[irp posts=”17100″]

شکل دهی برازش

اکثر الگوریتم‌هایی که در بخش‌های قبلیِ این مقاله اشاره شد، معمولاً با روشی موسوم به «شکل‌دهی برازش» یا «Fitness Shaping» ترکیب می‌شوند؛ مثل شکل‌دهی برازش رتبه‌محور based-ranked fitness shaping method که در این بخش معرفی خواهد شد. «شکل‌دهی برازش» این فرصت را به ما می‌دهد تا از دخالت داده‌های دورافتاده outlier در جمعیت جلوگیری کنیم و محاسبه گرادیان تقریبی بدون هیچ مشکل خاصی پیش رود:

اگر در جمعیت F(z^m)F(zm) خیلی بزرگتر از F(zi) باشد، شاید گرادیان تحت تاثیر داده‌های دورافتاده قرار گیرد. همچنین احتمالِ گیر افتادنِ الگوریتم در بهینه محلی افزایش پیدا کند. برای رهایی از این مشکل می‌توانیم از یک تبدیل رتبه بر روی برازش‌ها استفاده کنیم.

در این روش به جای استفاده از تابع برازش اصلی، نتایج را مرتب می‌کنیم. سپس از یک تابع برازش افزوده شده که متناسب است با رتبه راه‌حل‌ها در جمعیت جواب، استفاده می‌کنیم. در شکل زیر مقایسه‌ای میان مجموعه اصلی برازش و برازش مرتب شده نشان داده شده است.

همانطور که در شکل فوق قابل مشاهده است، جمعیت جواب ها دارای 101 جواب است. در این حالت ابتدا هر یک از جواب‌ها بوسیله تابع برازش اصلی ارزیابی می‌شود، سپس جواب‌ها بر اساس برازش‌شان مرتب می‌شوند. در این مرحله مقدار برازش افزوده شده -0.5 به بدترین جواب، -0.49 به دومین بدترین، …، 0.49 به دومین بهترین و 0.5 به بهترین جواب اختصاص داده می‌شود.

این مجموعه برازش‌های افزوده شده بجای برازش‌های حاصل از تابع ارزیابی واقعی، برای محاسبۀ به‌روزرسانیِ گرادیان استفاده خواهد شد. این روش تا حد زیادی به به‌کارگیری روش نرمال‌سازیِ باخ Batch Normalization در نتایج شباهت دارد.

روش‌های جایگزینی برای شکل‌دهی برازش وجود دارد، اما همه آن‌ها اساساً در پایان به نتایج مشابهی می‌رسند. اگر تابع هدف برای یک شبکه سیاست داده شده، غیر قطعی non-deterministic باشد، شکل‌دهی برازش می‌تواند در کارهای RL خیلی مفید باشد، چرا که در این نوع محیط‌ها شاهد ایجاد تصادفیِ نقشه‌ها هستیم و مخالفان، سیاست‌های تصادفی در پیش می‌گیرند. این روش کارآیی چندانی در بهینه‌سازیِ توابع جبری قطعی که رفتار خوبی دارند، ندارد. استفاده از این روش می‌تواند زمان لازم برای رسیدن به راه‌حل مناسب را نیز افزایش دهد.

MNIST

استراتژی تکاملی می‌تواند روش خوبی برای جستجوی راه‌حل‌های جدید بیشتری باشد که یافتن‌شان با روش‌های گرادیان‌محور دشواری‌های زیادی به همراه دارد. اما کماکان عملکرد بسیار ضعیفی در انجام خیلی از مسائل دارد.

برای مثال، تنها یک فرد ناشی می‌تواند از الگوریتم ژنتیک برای دسته‌بندی عکس استفاده کند. اما گاهی این افراد در دنیا وجود دارند و گاهی نیز این بررسی‌ها مفید هستند.

همه الگوریتم‌های ML باید در MNIST مورد آزمایش قرار گیرند. در نتیجه سعی کردیم الگوریتم‌های گوناگون استراتژی تکاملی که در این مقاله توضیح داده شد را برای یافتن وزن های یک convnet دو لایه کوچک جهت دسته بندی عکس، بکار ببریم و بررسی کنیم. عملکرد این روش‌ها در مقایسه با SGD چگونه است. «convnet» حدود یازده هزار پارامتر دارد. بنابراین می‌توانیم از الگوریتم CMA-ES استفاده کنیم. کدها و آزمایش‌ها در این بخش قابل دسترس هستند.

نتایج روش‌های گوناگونِ استراتژی تکاملی در بخش زیر بیان شده‌اند که در آنها اندازه جمعیت جواب‌ها 101 مورد است. همچنین تعداد تکرارها نیز 300 دوره در نظر گرفته شده است. آن دسته از پارامترهای مدل را زیر نظر داریم که بهترین عملکرد را در پایان هر دوره بر روی کل مجموعه آموزشی دارند و ارزیابی این مدل بر روی داده‌های آزمایش پس از اتمام 300 تکرار انجام می‌گیرد. جالب است که گاهی دقت مجموعه آزمایش در مدل‌هایی که امتیاز پایینی دارند، بالاتر از مجموعه آموزشی است.

نمی‌توان این نتایج را به طیف گسترده تعمیم داد. چرا که نباید به یک دوره عملیات اکتفا کرد. همچنین نباید به طور متوسط نیاز به انجام 5 تا 10 عملیات است. نتایجی که بر پایه یک دوره عملیات باشند، نشان می‌دهند که الگوریتم «CMA-ES» بهترین عملکرد را بر روی MNIST دارد. اما عملکرد الگوریتم PEPG نیز چندان تفاوتی با آن ندارد.

هر دوی این الگوریتم‌ها حدود 98 درصد از دقت آزمایش را کسب کرده‌اند؛ یعنی یک درصد کمتر از مبنای «SGD/ADAM». شاید قابلیت تغییر پویایِ ماتریس کوواریانس و پارامترهای انحراف معیار در هر نسل باعث شده تا وزن‌ها را بهتر از نسخۀ ساده‌تر «OpenAI» تنظیم کنند.

خودتان امتحان کنید

شاید همه الگوریتم‌هایی که در مقاله حاضر معرفی شدند به صورت منبع آزاد در دسترس باشند. «نیکولاس هنسن» نویسنده «CMA-ES» یک پیاده‌سازی مبتنی بر numpy را برای CMA-ES ارائه داده است.

با استفاده از پیاده سازی ایشان، الگوریتم های دیگری مانند الگوریتم ژنتیک ساده، PEPG و OpenAI’s را پیاده‌سازی نمودم. همچنین در در یک فایل پایتون کوچک به نام es.py قرار دادم. با این روش من می‌توانم تنها با تغییر یک خط کد، به راحتی الگوریتم های ES را با یکدیگر مقایسه کنم.

import es
#solver = es.SimpleGA(...)
#solver = es.PEPG(...)
#solver = es.OpenES(...)
solver = es.CMAES(...)
while True:
solutions = solver.ask()
fitness_list = np.zeros(solver.popsize)
for i in range(solver.popsize):
fitness_list[i] = evaluate(solutions[i])
solver.tell(fitness_list)
result = solver.result()
if result[1] > MY_REQUIRED_FITNESS:
break

می‌توانید به فایل «es.py» در «GitHub» و نمونه‌های نوت‌بوک «IPython» نگاه کنید. در نوت‌بوک «IPython»، که با es.py همراه است. من نشان دادم که چگونه میتوان از ES جهت حل تابع Rastrigin با بیش از 100 بعد که دارای نقاط بهینه محلی بیشتری است، استفاده شود. توجه شود که مسئله 100 بعدی بسیار پیچیده‌تر از مسئله دو بعدی است که در مثال‌های این مقاله آورده شد. در شکل زیر مقایسه عملکرد الگوریتم‌های ES بر روی مسئله 100 بعدی Rastrigin آورده شده است.

در مسئله 100 بعدی «Rastrigin» هیچ یک از ابزارهای بهینه‌ساز به راه‌حل بهینه سراسری نرسیده‌اند. اگرچه الگوریتم «CMA-ES» عملکرد خوبی داشته است.

PEPG در جایگاه دوم قرار گرفت و OpenAI-ES و الگوریتم ژنتیک در جایگاه‌های بعدی قرار گرفتند. باید به تدریج σ را در OpenAI-ES کاهش می‌دادیم تا عملکرد خوبی در این کار داشته باشد: