فشرده سازی شبکه عصبی: مقدمه‌ای بر هرس وزن، کوانتیزه کردن و تقطیر دانش

در این مقاله روش فشرده سازی شبکه عصبی را توضیح می‌د هیم. معماری‌های مدرن و نوآورانه‌ی شبکه‌های عصبی از اهمیت بسیار زیادی برخوردار هستند. برای مثال شاید با GPT-3، جدیدترین مدل تحولی فناوری پردازش زبان طبیعی (NLP) که OpenAI ارائه داده، آشنایی داشته باشید. این مدل قادر به نوشتن شعر و داستان‌گویی تعاملی (محاوره‌ای) است.

GPT-3 حدود 175 بیلیون پارامتر دارد.

برای درک بهتر بزرگی این عدد، به این مثال توجه کنید. عرض یک اسکناس 100 دلاری تقریباً 6.14 اینچ (15.59 سانتی‌متر) است. اگر این تعداد اسکناس را کنار هم روی زمین بگذارید خطی به اندازه‌ 169586 مایل (272922.212 کیلومتر) خواهید داشت. شعاع زمین 24901 مایل (40074.275 کیلومتر) است.پس می‌توانیم بگوییم با این مقدار اسکناس می‌توانیم حدود 6.8 بار دور زمین بچرخیم.

اما باید توجه داشته باشیم که تعداد بالای پارامترها نکته‌ مثبتی نیست. هرچند پارامترهای بیشتر به معنی نتایج بهتر است، هزینه‌های زیادی هم به دنبال خواهد داشت. مدل GPT-3 بهflops  3.14E+23 زمان آموزش نیاز داشت و هزینه‌ محاسباتی آن هم به چندین میلیون دلار رسید.

GPT-3 آنقدر بزرگ است که نمی‌تواند به آسانی به سایر دستگاه‌ها منتقل شود. دسترسی به این مدل اکنون از طریق رابط برنامه‌ی کاربردی OpenAI امکان‌پذیر است، اما نمی‌توانید به سادگی یک منبع‌کد GitHub از آن درست کنید و روی کامپیوتر خود اجرا نمایید.

البته آنچه بیان شد تنها یک سر مسئله است. کاربرد مدل‌های کوچک هم خود چالش عظیمی برای مهندسان یادگیری ماشین به شمار می‌رود. مدل‌های کوچک و سریع در عمل از مدل‌های سنگین خیلی بهتر هستند.

به همین دلیل پژوهشگران و مهندسان انرژی زیادی روی فشرده سازی شبکه عصبی صرف می‌کنند. به دنبال این تلاش‌ها چندین روش به دست آمده‌اند.

چرایی و چگونگی

با بررسی مجدد GPT-3 متوجه خواهیم شد تعداد پارامترها و زمان آموزش بر عملکرد تأثیر می‌گذارد.

رویه واضح است: تعداد زیاد پارامترها منجر به عملکرد بهتر و در عین حال هزینه‌های محاسباتی بیشتر می‌شود. هزینه‌های بالا بر زمان آموزش، هزینه‌های سرور و محیط زیست تأثیر خواهد داشت. با این حال آموزش تنها قسمت اول چرخه‌ زندگی شبکه های عصبی است. در قسمت‌های بعد هزینه‌های استنتاج Inference costs جای هزینه‌ آموزش را می‌گیرند.

به منظور بهینه‌سازی این هزینه‌ها از طریق فشرده سازی شبکه عصبی سه روش اصلی وجود دارد:

• هرس وزن
• کوآنتیزه کردن
• تقطیر دانش

در این مقاله قصد داریم این روش‌ها را معرفی کرده و از نحوه‌ کار آن‌ها توضیح مختصری ارائه دهیم.

هرس وزن

یکی از قدیمی‌ترین روش‌های فشرده سازی شبکه‌ عصبی هرس وزن است که به حذف اتصالات خاصی بین نورون‌ها اشاره دارد. این حذف در عمل به این معناست که وزن حذف شده با صفر جایگزین می‌شود.

این ایده شاید در نگاه اول تعجب‌برانگیز به نظر برسد و این سؤال برایتان مطرح شود که آیا این کار باعث از دست رفتن دانشی که شبکه‌ عصبی آموخته نمی‌شود؟

البته که همینطور است. حذف همه‌ اتصالات منجر به از دست دادن آنچه آموخته شده خواهد شد. اما هرس یک اتصال به تنهایی باعث کاهش دقت نخواهد شد.

سؤال این‌جاست که تا کجا می‌توانید این اتصالات را حذف کنید تا به عملکرد پیش‌بینی آسیبی نرسد؟

آسیب مغزی بهینه

یان لکان Yann LeCun، جان اس‌دنکر  John S. Denker و سارا ای‌سولا  Sara A. Solla (1990) اولین پژوهشگرانی بودند که در مقاله‌ خود به نام آسیب مغزی بهینه به این پرسش پرداختند. آن‌ها یک روش دوره‌ای (تکراری) را طراحی کردند که مراحل آن عبارت‌اند از:

1. آموزش شبکه؛
2. برآورد میزان اهمیت هرکدام از وزن‌ها با مشاهده‌ چگونگی تغییر تابع زیان هنگام تغییر و درهم‌ریختن وزن Weight perturbing. هرچه این تغییر کوچک‌تر باشد نشان‌دهنده‌ اهمیت کمتر آن وزن است (به این میزان اهمیت برجستگی Saliency گفته می‌شود)؛
3. حذف وزن‌های کم‌اهمیت؛
4. برگشت به گام اول، آموزش مجدد شبکه و تغییر دائمی وزن‌های حذف شده به صفر.

این پژوهشگران طی آزمایشاتی که روی هرس شبکه‌ LeNet (آموزش دیده روی دیتاست MNIST) انجام دادند دریافتند بخش عظیمی از وزن‌ها را می‌توان بدون افزایش معنادار در تابع زیان حذف نمود.

آموزش مجدد بعد از هرس اقدامی ضروری اما دشوار محسوب می‌شود، زیرا کوچکی مدل به معنی ظرفیت کمتر آن است. به علاوه همانطور که بالاتر بیان شد، بخش بزرگی از هزینه‌های محاسباتی مربوط به آموزش است. پس این روش فشرده سازی شبکه عصبی تنها به زمان استنتاج کمک خواهد کرد.

آیا روش هرسی وجود دارد که نیازمند آموزش کمتری پس از هرس باشد اما در عین حال به عملکرد پیش‌بینی مدل هرس‌نشده دست یابد؟

فرضیه‌ بلیط لاتاری

در سال 2008، پژوهشگران MIT به کشف عظیمی رسیدند. جاناتان فرنکل و مایکل کاربین Johnathan Frankle and Micheal Carbin در مقاله‌ خود به نام فرضیه‌ بلیط لاتاری می‌گویند:

یک شبکه‌ عصبی متراکم که به صورت تصادفی تعریف شده، زیرشبکه‌ای را در خود دارد که به نحوی تعریف شده که (وقتی به تنهایی آموزش می‌بیند) می‌تواند بعد از (حداکثر) تعداد مساوی تکرار، به میزان دقت شبکه‌ اصلی دست یابد.

این زیرشبکه‌ها را بلیط‌های برنده‌ی لاتاری می‌نامند. برای این‌که دلیل این نام‌گذاری را بفهمید فرض کنید بلیط لاتاری گرفته‌اید (عددی که از تعداد اتم‌های موجود در کل جهان بیشتر است). چون تعداد خیلی زیادی بلیط دارید احتمال این‌که برنده‌ لاتاری نباشید خیلی کم است. این موضوع شبیه آموزش یک شبکه‌ عصبی است که در آن وزن‌ها را به صورت تصادفی تعریف می‌کنیم.

اگر این فرضیه درست باشد و چنین زیرشبکه‌هایی را بتوان پیدا کرد، آموزش می‌تواند خیلی سریع‌تر و ارزان‌تر انجام شود. چون یک گام تکرار به تنهایی به محاسبه‌ کمتری نیاز خواهد داشت.

سؤال اینجاست که، با فرض درست بودن این فرضیه، چطور می‌توانیم به چنین زیرشبکه‌هایی دست یابیم؟ نویسندگان بدین منظور این روش تکراری را پیشنهاد می‌کنند:

1. تعریف تصادفی شبکه و ذخیره‌سازی وزن‌های تعریف‌شده برای رجوع در آینده؛
2. آموزش شبکه در تعداد مشخصی مرحله؛
3. حذف درصدی از وزن‌ها با کوچکترین مقدار؛
4. ذخیره‌سازی مجدد وزن‌های باقیمانده با مقداری که طی تعریف اولیه ارائه شده بود؛
5. بازگشت به گام دوم و تکرار هرس.

این روش برای معماری‌های ساده که روی دیتاست‌های ساده آموزش دیده‌اند (همچون LeNet روی دیتاست MNIST) پیشرفت چشمگیری به همراه دارد (همانطور که در شکل پایین مشاهده می‌کنید).

در هر صورت با وجود این‌که این فرضیه امیدوارکننده به نظر می‌رسید، روی معماری‌های پیچیده‌تر (همچون ResNets) عملکرد خوبی نداشت. علاوه بر این بعد از آموزش هم هرس لازم است که خود یک مشکل به حساب می‌رود.

SynFlow

این مورد جدیدترین الگوریتم هرس قبل از آموزش است که در سال 2020، توسط هیدنوری تاناکا، دنیل کنین، دنیل ال‌کی‌یامینز و سریا گنگولی Hidenori Tanake, Daniel Kunin, Daniel L. K. Yasmin and Surya Ganguli (از دانشگاه استنفورد) ارائه شد. این پژوهشگران روشی را معرفی می‌کنند که فراتر رفته و هرس بدون آموزش را مطرح می‌نماید.

آنها ابتدا مفهوم فروپاشی لایه Layer Collapse را معرفی می‌کنند:

هرس ناآگاهانه, سراسر یک لایه‌ که شبکه را غیرقابل آموزش خواهد کرد.

این مفهوم در نظریه‌ی مذکور نقش مهمی ایفا می‌کند. الگوریتم‌های هرس باید از فروپاشی لایه پرهیز کنند. قسمت سخت کار تشخیص رده‌ای از الگوریتم‌هاست که این معیار را برآورده کنند.

نویسندگان بدین منظور مقدار برجستگی سیناپسی Synaptic Salience Scores یا مقدار گرادیان را معرفی و برای هر وزن آن را تعیین می‌نمایند:

در این فرمول L تابع زیان خروجی شبکه و w پارامتر وزن است. هر نورون این خاصیت را دارد: تحت شرایط خاص برای توابع فعال‌سازی، مجموع مقادیر گرادیان ورودی برابر است با مجموع مقادیر گرادیان خروجی.

این مقدار برای انتخاب وزن‌هایی که باید هرس شوند مورد استفاده قرار می‌گیرد (اگر به خاطر داشته باشید در روش آسیب مغزی بهینه، از یک مقدار جایگشت-محور Perturbation-based quantity و در فرضیه‌ بلیط لاتاری هم از بزرگی magnitude بدین منظور استفاده می‌شد).

دریافته‌اند که مقادیر گرادیان بین لایه‌ها نگه داشته می‌شود. اگر یک الگوریتم هرس تکراری به نگهداری این مقدار بین لایه‌ای اهمیت دهد، می‌توان از فروپاشی لایه جلوگیری کرد.

الگوریتم SynFlow یک الگوریتم هرس تکراری (شبیه به الگوریتم‌های قبلی) است که انتخاب (وزن‌ها) در آن بر اساس مقادیر گرادیانی صورت می‌گیرد.

اما کار هنوز تمام نشده است. همانطور که جاناتان فرنکل و همکارانش در مقاله‌ اخیر خود خاطرنشان می‌کنند، هیچ راهکاری وجود ندارد که در همه‌ مواقع پاسخگو باشد. هر روشی در سناریوها و موقعیت‌های خاصی از سایر روش‌ها عملکرد بهتری دارد. علاوه بر این، روش‌های هرس پیش از آموزش از خط پایه (هرس‌های تصادفی) عملکرد بهتری دارند، با این حال به خوبی برخی از الگوریتم‌های پس‌آموزشی (به خصوص هرس مبتنی بر بزرگی) نیستند.

پیاده‌سازی و اجرا

هرس در تنسورفلو و پای تورچ قابل دسترس می‌باشد.

Pruning Tutorial – PyTorch Tutorials 1.6.0 documentation

TensorFlow Model Optimization Toolkit – Pruning API

در قسمت بعدی به یک روش فشرده‌سازی شبکه عصبی دیگر خواهیم پرداخت.

کوانتیزه کردن

ذات یک شبکه‌ عصبی جمعی از جبر خطی Linear algebra و برخی دیگر از عملیات‌هاست. بیشتر سیستم‌ها به صورت پیش‌فرض از انواع فرمت‌های float32  برای معرفی متغیرها و وزن‌ها استفاده می‌کنند.

با این حال سرعت محاسباتی با فرمت‌های دیگر مثل int8 عموماً بیشتر از فرمت‌های float32  است و ردپای کمتری هم در حافظه به جای می‌گذارند. البته این موضوع به سخت‌افزار هم بستگی دارد، اما در این نوشتار وارد جزئیات آن نخواهیم شد.

کوانتیزه کردن شبکه‌ عصبی به روش‌هایی اشاره دارد که از این موضوع بهره می‌گیرند. برای مثال اگر می‌خواهیم از فرمتfloat32   به int8 برویم و مقادیر ما در بازه‌ی [-a, a]  باشند ( a یک عدد حقیقی)، می‌توانیم برای تبدیل وزن‌ها از تبدیل پایین استفاده کنیم و با محاسبات در فرمت جدید کار را ادامه دهیم.

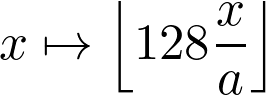
البته کار به این سادگی هم نیست. ضرب دو عدد int8 می‌تواند به آسانی به int16 سرریز overflow شده و این روند همینطور ادامه یابد. مشکل گذشته درمورد یافتن تبادل بهینه همچنان وجود دارد.

در روش کوانتیزه کردن دو عامل اصلی وجود دارد: کوانتیزه کردن پس-آموزشی Post-training quantization و آموزش مبتنی بر کوانتیزه Quantization-aware training. مورد اول مستقیم‌تر است اما می‌تواند به افزایش چشمگیری در تابع زیان دقت مدل منجر شود.

همانطور که در جدول بالا مشاهده می‌کنید، روش کوانتیزه کردن می‌تواند زمان استنتاج را در برخی نمونه‌ها به نیم کاهش دهد. با این حال تبدیل فرمت float32  به int8 انتقال آسانی نخواهد بود. به همین دلیل در صورتی که نمای گرادیانی Gradient landscape وسیع باشد، امکان دستیابی به نتایج زیربهینه وجود دارد.

با آموزش مبتنی بر کوانتیزه کردن قادر به بهبود زمان آموزش هم خواهیم بود.

پیاده‌سازی و اجرا

روش کوانتیزه کردن هم مثل روش هرس وزن، در تنسورفلو و پای تورچ در دسترس می‌باشد.

Model optimization | TensorFlow Lite

Quantization – PyTorch 1.6.0 documentation

در زمان نوشتن این مقاله، پیاده‌سازی در PyTorch به صورت آزمایشی است، یعنی امکان تغییر وجود دارد. پس باید منتظر تغییرات متحول‌کننده در نسخه‌های پیش رو باشید.

روش‌هایی که تا اینجا بررسی کردیم یک اصل مشترک داشتند و آن آموزش شبکه و دورانداختن برخی اطلاعات به منظور فشرده‌سازی آن بود. اما روش سوم، تقطیر دانش، از این نظر کاملاً متفاوت است.

تقطیر دانش

با این‌که کوانتیزه کردن و هرس می‌توانند کارآمد باشند، در نهایت مقداری آسیب هم وارد می‌کنند. به همین دلیل جفری هینتون، اریل وینیالز و جف دین Geoffrey Hinton, Oriol Vinyals and Jeff Dean در مقاله‌ خود به نام تقطیر دانش در شبکه‌ عصبی، رویکردی جایگزین مطرح کردند.

ایده‌ی زیربنایی این رویکرد ساده است: یک مدل بزرگ (معلم) را آموزش دهید تا به عملکرد خوبی دست یابد و سپس از پیش‌بینی‌های آن برای آموزش یک شبکه‌ کوچک‌تر (دانش‌آموز) استفاده کنید.

مطالعات این نویسندگان در زمینه فشرده سازی شبکه عصبی نشان داده که با این روش می‌توان مدل‌های گروهی Ensemble model بزرگ را فشرده‌سازی کرد تا به معماری‌های ساده‌تر و بهره‌وری مناسب‌تر دست یافت.

با روش تقطیر دانش زمان استناج مدل‌های تقطیرشده، و نه زمان آموزش آن‌ها، را می‌توان بهبود بخشید. این نکته وجه تمایز اصلی این روش با دو روش قبلی است، زیرا آموزش می‌تواند بسیار هزینه‌بر باشد (اگر همان مثال GPT-3 را درنظر بگیریم، می‌توانیم میلیون‌ها دلار صرفه‌جویی کنیم).

ممکن است از خود بپرسید چرا از همان ابتدا از یک معماری فشرده استفاده نکنیم؟ راز کار، آموختن تعمیم‌پذیری معلم به دانش‌آموز با استفاده از پیش‌بینی‌های معلم است. مدل دانش‌آموز علاوه بر داده‌های آموزشی، داده‌های جدیدی را هم دریافت می‌کند که برای نزدیک شدن به خروجی معلم مفید خواهند بود.

جدول بالا نتایج روش تقطیر دانش را روی یک مدل تشخیص گفتار نشان می‌دهد. این آزمایش در مقاله‌ تقطیر دانش در یک شبکه‌ عصبی توسط جفری هینتون، اریل وینیالز و جف دین انجام شده است.

هرچه مدل کوچک‌تر باشد، داده‌های آموزشی بیشتری نیاز است تا قادر به تعمیم‌پذیری  خوب باشد. بنابراین ممکن است به یک معماری پیچیده (مثل یک مدل گروهی) نیاز داشته باشیم تا بتوانیم به عملکرد خارق‌العاده‌ای روی مسائل پیچیده دست یابیم. با این حال همچنان می‌توان از دانش آن استفاده کرد تا عملکرد مدل دانش‌آموز را از خط‌پایه فراتر برد.

یکی از اولین موارد استفاده از تقطیر دانش، فشرده سازی شبکه عصبی و مدل‌های گروهی و مناسب‌سازی بهره‌وری آن‌ها می‌باشد. مدل‌های گروهی در رقابت‌های Kaggle شهرت بدی به دست آوردند. چندین مدل برنده که از مدل‌های کوچک‌تری تشکیل شده بودند به نتایج بسیار خوبی دست یافتند اما در عمل بلااستفاده بودند.

روش تقطیر دانش پس از آن در معماری‌های دیگر، به ویژه BERT که مدل مبدل مشهوری در حوزه‌ پردازش زبان طبیعی است، با موفقیت اجرا شد.

به غیر از رویکرد خط‌پایه‌ تقطیر که توسط هینتون و همکارانش ارائه گردید، روش‌های دیگری هم وجود دارند که سعی در پیش‌برد این رویکرد دارد.

پیاده‌سازی و اجرا

از آن‌جایی که تقطیر دانش (مثل روش هرس یا کوانتیزه کردن) دستکاری وزن‌ ندارد، می‌تواند در هر چارچوبی اجرا گردد. چندین نمونه را در این قسمت بیان می‌کنیم.

Keras documentation: Knowledge Distillation

AberHu/Knowledge-Distillation-Zoo

Pytorch implementation of various Knowledge Distillation (KD) methods. This repository is a simple reference, mainly…

نتیجه‌گیری

حوزه‌ فشرده سازی شبکه عصبی همزمان با بزرگ‌تر شدن آن‌ها، اهمیت بیشتری پیدا می‌کند و همان‌طور که مسائل و معماری‌ها پیچیده‌تر می‌شوند، هزینه‌ محاسبات و اثرات بر محیط زیست هم افزایش می‌یابد.

این روند رو به تسریع است؛ برای مثال GPT-3 را که 175 بیلیون پارامتر دارد (که یک جهش 10x در بزرگی آن محسوب می‌شود) با مدل‌های بزرگ قبل از آن مقایسه کنید. می‌توان نتیجه گرفت فشرده سازی شبکه عصبی یک مسئله‌ بنیادی بوده و در آینده اهمیت بیشتری هم خواهد یافت.