آشنایی با تکنیک تحلیل مؤلفه اصلی و نقش آن در کشف ترندهای زیربنایی موجود در داده‌ها

در رشته‌های علوم کمی و محاسباتی، از جمله حوزه‌های مالی و علوم داده، سعی بر این است که با جستجو در میان داده‌هایی با نویز فراوان، یک سیگنال کشف شود. الگوریتم PCA یا تحلیل مؤلفه اصلی Principal Components Analysis به ما کمک می‌کند محرک‌های نهفته در داده ها را پیدا کنیم؛ این محرک‌ها، ویژگی‌های مفیدی هستند که ما را قادر می‌سازند مجموعه عظیمی که از ویژگی‌ها داریم را تنها با استفاده از چند مؤلفه اصلی، خلاصه‌سازی کنیم.

برای مشاهده‌ کد به کاررفته برای رسم نمودارها، به این لینک مراجعه کنید.

واریانس، شمشیری دولبه

اگر با مبنای نظری آمار و علوم داده آشنایی داشته باشید، حتماً می‌دانید که هدف اصلی از ساخت مدل‌ها، توضیح واریانس مشاهده‌شده در داده‌هاست.

در این نوشتار، به صورت گام به گام معنی این جمله را با هم بررسی می‌کنیم. قبل از هرچیز، باید بفهمیم منظور از واریانس چیست. فرض کنید داده‌هایی با این شکل در اختیار دارید:

پیش‌بینی یک خط صاف کار آسان، و البته بیهوده‌ای است؛ چون مقدار آن همیشه یک عدد (در تصویر بالا 5) است. خط صاف مثال خوبی برای داده‌هایی است که واریانس صفر دارند؛ این داده‌ها هیچ پراکندگی در محور عمودی ندارند.

برای درک بهتر داده‌هایی که واریانس صفر دارند، مثالی از دنیای واقعی ذکر می‌کنیم: فرض کنید رئیستان به شما می‌گوید تعداد طبقات یک ساختمان پنج طبقه را پیش‌بینی کنید (با این‌که از نظر منطقی، کار معناداری نیست!). اگر 100 روز پشت سر هم تعداد طبقات این ساختمان را اندازه بگیرید، در آخر نموداری مثل تصویر بالا به او تحویل خواهید داد. وقتی رئیستان بخواهد پیش‌بینی شما در مورد تعداد طبقات ساختمان را بداند، با اطمینان خاطر پاسخ می‌دهید: «فردا هم ساختمان 5 طبقه خواهد داشت!»

احتمال درست بودن پیش‌بینی شما 100% است، مگر این‌که اتفاق خاصی (مثلاً زلزله) رخ دهد. اما همانطور که گفتیم این پیش‌بینی هیچ ارزش و فایده‌ای ندارد. چون داده‌هایی که واریانس ندارند، هیچ ابهامی هم نخواهند داشت؛ به همین دلیل چیزی برای پیش‌بینی یا توضیح باقی نمی‌ماند. به بیان دیگر، اگر واریانس متغیر X یا پیش‌بین (متغیری که برای پیش‌بینی متغیر هدف به کار می‌رود) صفر باشد، هیچ سیگنالی از مجموعه‌ی ویژگی به دست نمی‌آوریم.

حال برای توضیح داده‌های واریانس‌دار، از یک مثال دیگر استفاده می‌کنیم: بازده روزانه سهام اپل طی یک بازه‌ 100 روزه.

داده‌های مربوط به این مسئله واریانس بالایی دارند. واریانس را می‌توان همین نوساناتی در نظر گرفت که در نمودار مشاهده می‌کنید. هرچه واریانس بیشتر باشد، پیش‌بینی و توضیح آن دشوارتر خواهد بود. همانطور که در نمودار بالا مشاهده می‌کنید، بازده روزانه‌ی سهام اپل نوسانات چشم‌گیری دارد و بین مقادیر منفی و مثبت جابجا می‌شود.

اما در میان این داده‌های پر از نوسان و نویز، سیگنال یا اطلاعاتی هم وجود دارد.

متغیر هدفی که واریانس بالا دارد، جالب‌تر است و متغیر پیش‌بینی که واریانس داده‌های آن زیاد است، اطلاعات بیشتری در اختیار قرار می‌دهد.

به همین خاطر است که می‌گوییم واریانس یک شمشیر دولبه است:

• از یک سو، هرچه واریانس متغیر هدف بیشتر باشد، عدم اطمینان افزایش می‌یابد و به تبع، پیش‌بینی و توضیح متغیر هدف دشوارتر خواهد شد.
• از سوی دیگر، ویژگی‌هایی که واریانس ندارند، اصلاً جالب نیستند و هیچ سیگنالی در بر ندارند. برای ساخت یک مدل باکیفیت، به ویژگی‌هایی نیاز داریم که سیگنال داشته باشند؛ بنابراین واریانس این ویژگی‌ها باید بالا باشد. ویژگی‌هایی مطلوب هستند که کوواریانس آن‌ها با متغیر هدف صفر نباشد.

ثبت سیگنال به کمک مؤلفه اصلی

دنیایی که در آن زندگی می‌کنیم پر از اطلاعات است. حوزه‌ی علوم داده هم از این قانون مستثنی نیست؛ به شکلی که برای پیش‌بینی یک متغیر، همیشه یک مجموعه‌ویژگی خیلی بزرگ در دست داریم.

اما حتی اگر بخواهیم هم نمی‌توانیم از همه‌ی این ویژگی‌ها استفاده کنیم، چون به تعداد کافی مشاهده نداریم. به عنوان مثال، اگر تعداد مشاهداتی که از متغیر هدف داریم 5000 باشد، نمی‌توانیم برای برازش مدل از 10 هزار ویژگی استفاده کنیم. زیرا در این صورت مدلی به شدت بیش‌برازش شده به دست می‌آوریم که به محض اجرا در دنیای واقعی (روی داده‌هایی کاملاً متفاوت از نمونه‌های آموزشی) با شکست مواجه خواهد شد.

در هر صورت، اگر تجربه‌ای در مدلسازی یا دانشی در حوزه‌ی تخصصی مربوطه نداشته باشیم (و گاهی هم علی‌رغم در دست داشتن هردو) به سختی می‌توانیم ویژگی‌هایی که باید در مدل باقی بمانند را انتخاب کنیم. به همین دلیل، به الگوریتمی نیاز داریم که بتواند 10 هزار ویژگی را به یک مجموعه‌ویژگی ایده‌آل تبدیل کند.

مجموعه‌ویژگی ایده‌آل

برای ساخت یک مجموعه‌ی ایده‌آل از ویژگی‌ها، توجه به سه خاصیت ضروری است:

1. 1. واریانس بالا: هرچه واریانس ویژگی‌ها بالاتر باشد، به طور بالقوه اطلاعات بیشتری در بردارند. سیگنال یا اطلاعات مفید حاصل از ویژگی‌ها، ملزومه‌ی ساخت یک مدل باکیفیت هستند.
2. 2. عدم همبستگی: ویژگی‌هایی که همبستگی زیادی با هم دارند، کمک چندانی به ما نخواهند کرد و حتی می‌توانند مضر هم باشند (وقتی همبستگی آنقدر بالاست که منجر به هم‌خطی بودن چندگانه Multi-collinearity می‌شود). برای درک بهتر این موضوع از یک مثال استفاده می‌کنیم: فرض کنید می‌خواهید یک گروه معامله‌گر حرفه‌ای استخدام کنید. آیا ترجیح می‌دهید همه‌ی آن‌ها به یه شکل سرمایه‌گذاری کنند یا متفاوت از هم؟ منطقی‌تر است که این افراد تا حد امکان از هم متفاوت باشند؛ بدین ترتیب، نوعی گوناگونی و پراکندگی به وجود می‌آید که در اثر آن، همه‌ی معامله‌گران دچار یک خطای مشابه نخواهند شد. به همین دلیل، اگر سهامی با ضرر روبرو شود، همه‌ی افراد تأثیر نمی‌پذیرند.
3. 3. تعداد پایین: در حالت ایده‌آل، تعداد ویژگی‌ها کمتر از تعداد مشاهدات موجود در متغیر هدف است. زیاد بودن تعداد ویژگی‌ها نسبت به مشاهدات منجر به بیش‌برازش مدل می‌شود؛ در این صورت، مدل روی داده‌هایی غیر از نمونه‌های آموزشی، عملکردی ضعیف خواهد داشت.

PCA مجموعه ویژگی‌های ایده‌آل را در اختیار ما قرار می‌دهد. این تکنیک مجموعه‌ای تولید می‌کند که در آن، مؤلفه اصلی بر حسب میزان واریانس مرتب شده‌اند (از زیاد به کم). مؤلفه‌های حاضر در این مجموعه با هم همبستگی ندارند و تعدادشان کم است (علاوه بر این، می‌توانیم مؤلفه‌هایی که در رتبه‌های پایین قرار گرفته‌اند را کنار بگذاریم، چون سیگنال کمی دربردارند).

نحوه کارکرد تحلیل مؤلفه اصلی

نحوه‌ی کارکرد PCA را می‌توان هم از منظر جبر خطی و هم به صورت شهودی توضیح داد. اینجا از رویکرد دوم استفاده می‌کنیم؛ برای مطالعه‌ توضیحات ریاضی به این مقاله مراجعه کنید.

PCA به صورت مکرر و پیوسته این سؤالات را مطرح کرده و به آن‌ها پاسخ می‌دهد:

1. 1. سؤالی که PCA در شروع فرآیند می‌پرسد این است که «قوی‌ترین ترند موجود در مجموعه‌ی ویژگی کدام است؟». اسم این ترند را مؤلفه‌ی 1 می‌گذاریم.
2. 2. سؤال بعدی این است که «دومین ترند قوی در مجموعه‌ی ویژگی که با مؤلفه‌ی 1 همبستگی نداشته باشد، کدام است؟». این ترند را مؤلفه‌ی 2 می‌نامیم.
3. 3. در گام بعد، PCA می‌پرسد: «سومین ترند قوی در مجموعه‌ی ویژگی که با مؤلفه‌ 1 و 2 همبستگی نداشته باشد، کدام است؟» این ویژگی، مؤلفه‌ی 3 نام دارد.
4. 4. این جریان همینطور ادامه می‌یابد.

اما PCA چطور این ترندها را پیدا می‌کند؟ به تصویر پایین دقت کنید:

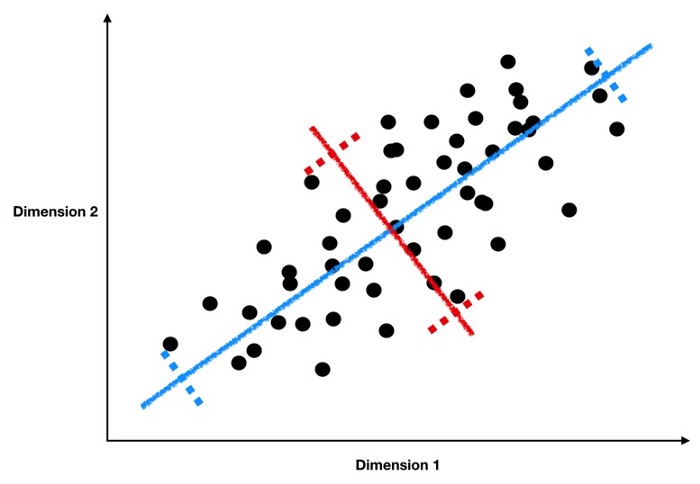
در این تصویر، نقاط سیاه‌رنگ نشان‌دهنده‌ داده‌ها هستند. حال سؤال اینجاست که قوی‌ترین ترند زیربنایی را چطور می‌توان پیدا کرد؟ برای یافتن پاسخ، از توضیحات مسائل رگرسیون خطی استفاده می‌کنیم: خطی که بهترین برازش را داشته باشد (یعنی خط آبی) قوی‌ترین ترند یا مؤلفه‌ی 1 خواهد بود. اما چرا خط قرمز را مؤلفه‌ی 1 در نظر نگرفتیم؟ اگر به خاطر داشته باشید، مؤلفه‌ی 1، مؤلفه اصلی است که بیشترین واریانس را دارد؛ چون هر چه واریانس بیشتر باشد، سیگنال‌های بالقوه‌ی آن مؤلفه بیشتر هستند.

شباهت این مسئله با رگرسیون خطی کمک می‌کند دریابیم هر کدام از مؤلفه‌های اصلی، ترکیبی خطی از ویژگی‌های واحد هستند. پس همانطور که مدل رگرسیون خطی، جمع وزن‌دهی‌شده‌ی ویژگی‌هایی است که کمترین فاصله را تا متغیر هدف دارند، مؤلفه اصلی را هم می‌توان جمع وزن‌دهی شده‌ی ویژگی‌ها در نظر گرفت. با این تفاوت که این‌جا، جمع وزن‌دهی شده‌ای را می‌خواهیم که به بهترین نحو ممکن ترندهای زیربنایی موجود در مجموعه ویژگی را به ما نشان دهد.

به مثال خود بر می‌گردیم. از روی نمودار درمی‌یابیم که خط آبی واریانس بیشتری نسبت به خط قرمز دارد. چون فاصله‌ی بین خط‌چین‌های آبی بیشتر از فاصله‌ی خط‌چین‌های قرمز است. فاصله‌ بین خط‌چین‌ها برآوردی از واریانسی را نشان می‌دهد که توسط مؤلفه اصلی به دست آمده است. هرچه تعداد نقاط سیاه‌رنگی که در اطراف مؤلفه اصلی پراکنده شده‌اند بیشتر باشد، واریانس بالاتر خواهد بود.

حال برای پیدا کردن مؤلفه‌ی 2، باید دومین ترند قوی را پیدا کنیم. همانطور که پیش‌تر گفته شد، در این گام یک شرط اضافی داریم: مؤلفه‌ی 2 نباید با مؤلفه‌ی 1 همبستگی داشته باشد. در آمار، ترندها و الگوهایی که بر هم عمود هستند، با یکدیگر همبستگی ندارند.

در تصویر بالا نمودار دو ویژگی (آبی و قرمز) را ترسیم کرده‌ایم. همانطور که مشاهده می‌کنید، این داده‌ها بر هم عمود هستند. به بیان دقیق‌تر، پراکندگی داده‌های ویژگی آبی‌رنگ عمود بر پراکندگی ویژگی‌ قرمزرنگ است. بنابراین، ویژگی‌های آبی‌رنگ به صورت افقی تغییر می‌کنند، ولی ویژگی قرمزرنگ کاملاً ثابت باقی می‌ماند، چون فقط به صورت عمودی می‌تواند تغییر کند.

پس برای پیدا کردن مؤلفه‌ی 2، باید دنبال مؤلفه‌ای باشیم که حداکثر واریانس ممکن را داشته باشد، و بر مؤلفه‌ی 1 نیز عمود باشد. مثالی که استفاده کردیم خیلی ساده بود و فقط دو بُعد داشت، به همین دلیل تنها یک گزینه برای انتخاب مؤلفه‌ 2 (خط قرمز) داشتیم. اما در واقعیت، هزاران ویژگی وجود دارد و برای پیدا کردن مؤلفه‌ها، باید در چندین بُعد جستجو را انجام دهیم. با این حال، کلیّت فرآیند به همین شکل انجام می‌گیرد.

مثالی برای شفاف‌سازی مطالب

به همان مثال بازده سهام برمی‌گردیم. اما اینجا، علاوه بر سهام اپل، از داده‌های مربوط به سهام 30 صنعت مختلف استفاده می‌کنیم. نمودار مربوط به بازده‌ روزانه‌ی همه‌ی این سهام‌ها طی یک بازه‌ی 100 روزه بدین شکل است:

همانطور که می‌بینید هر کدام از سهام‌ها مسیر خاص خودش را دارد و اطلاعات زیادی نمی‌توان از این نمودار دریافت. غیر از این‌که بازده‌ روزانه‌ی سهام‌ها بسیار متغیر و پر از نویز است. اکنون با استفاده از Sci-kit Learn، مؤلفه اصلی 1 را پیدا کرده و نمودار آن را رسم می‌کنیم. اما از آن‌جایی که همه‌ی ویژگی‌های این مثال مربوط به بازده روزانه‌ی سهام‌ها هستند، نیازی به مقیاس‌بندی آن‌ها نبود. در صورت لزوم، برای مقیاس‌بندی می‌توانید از StandardScaler یا MinMaxScaler استفاده کنید). خط مشکی که در تصویر پایین مشاهده می‌کنید، مؤلفه‌ی 1 را نشان می‌دهد:

در تصویر بالا، خط سیاه‌رنگ نشان‌دهنده‌ قوی‌ترین ترند زیربنایی بازده‌ روزانه‌ی سهام‌هاست. این ترند را بدون مشورت با متخصصان این حوزه نمی‌توان تفسیر کرد. تکنیک‌هایی همچون PCA که به منظور کاهش مجموعه‌های بزرگ ویژگی به مجموعه‌های کوچک‌تر و استخراج محرک‌های زیربنایی کلیدی به کار می‌روند، یک عیب بزرگ دارند. تفسیرپذیری را از بین می‌برند. تنها در صورتی می‌توانید مؤلفه‌های به دست آمده از PCA را تفسیر و درک کنید که بر حوزه‌ی تخصصی مربوطه تسلط داشته باشید.

اینجا به نظر می‌رسد مؤلفه‌ 1، یعنی قوی‌ترین ترند زیربنایی همه‌ داده‌های بازده سهام، مربوط به شاخص S&P 500 است؛ یعنی S&P 500 شاخص سراسری است که جذر و مد آن بر قیمت همه‌ی سهام‌ها تأثیر می‌گذارد. برای بررسی صحت این حدس، نموداری رسم می‌کنیم تا بازده روزانه‌ی S&P 500 را با مؤلفه‌ی 1 مقایسه کنیم. با این‌که داده‌ها نویز خیلی زیادی داشتند، این نمودار برازشی تقریباً عالی نشان می‌دهد؛ همبستگی بین سود روزانه S&P 500 و مؤلفه اصلی 1 برابر با 92/0 است.

پس نتیجه می‌گیریم حدس ما درست بود و مهم‌ترین ترند زیربنایی داده‌ها مربوط به بازار سهام است. پیاده‌سازی PCA در Sci-kit learn می‌تواند سهم همه‌ی مؤلفه‌ها در واریانس را نشان دهد. برای مثال، مؤلفه‌ی 1، 38% از کل واریانس مجموعه‌ی ویژگی را توجیه می‌کند.

حال یکی دیگر از مؤلفه‌های اصلی را بررسی می‌کنیم. در نمودار پایین، مؤلفه‌های 1 (سیاه‌رنگ) و 3 (سبزرنگ) را ترسیم کرده‌ایم. همانطور که انتظار داشتیم، همبستگی بین آن‌ها پایین است (08/0). بر خلاف مؤلفه‌ 1، مؤلفه‌ 3 تنها 9% از واریانس مجموعه ویژگی ما را توجیه می‌کند. این عدد از 38% مربوط به مؤلفه‌ی 1 خیلی کمتر است. متأسفانه هیچ نظری در مورد این‌که مؤلفه‌ 3 چه چیزی را نشان می‌دهد نداریم. مشکلی که باز هم به عدم تفسیرپذیری PCA برمی‌گردد.

جمع‌بندی

در این نوشتار آموختیم PCA چطور در کشف ترندهای زیربنایی داده‌ها به ما کمک می‌کند. این قابلیت در عصر کلان‌داده‌ها بسیار مفید و ارزشمند است. از جمله مزایای PCA می‌توان به این موارد اشاره کرد:

1. 1. سیگنال‌های بالقوه‌ی موجود در مجموعه‌ی ویژگی را ایزوله می‌کند تا بتوانیم از آن‌ها در مدل خود استفاده کنیم.
2. 2. تعداد ویژگی‌ها را کاهش داده و یک مجموعه‌ی کوچک‌تر از ترندهای زیربنایی کلیدی در اختیار ما می‌گذارد.

با این حال، این تکنیک معایبی هم دارد که بزرگ‌ترین آن‌ها را می‌توان از دست رفتن تفسیرپذیری ویژگی‌ها دانست. به همین دلیل، بدون تخصص و بدون گمانه‌زنی، نمی‌توانیم معنی هیچ کدام از این ویژگی‌ها را درک کنیم.

اما این مشکل چندان هم جدی نیست. اگر مطمئن هستید مجموعه‌ویژگی بزرگی که در دست دارید حاوی سیگنال‌های فراوانی است، الگوریتم PCA بسیار مفید بوده و شما را قادر می‌سازد بدون نگرانی در مورد بیش‌برازش، قسمت عمده‌ی این سیگنال را استخراج کرده و در مدل خود به کار ببرید.