
مقدمهای بر الگوریتم بیز ساده؛ توضیح قضیه بیز و ردهبند بیز ساده
برای آشنایی بهتر با بیز ساده بهنر است اینطور شروع کنیم. فرض کنید یک روز صبح از خواب بیدار میشوید و احساس کسالت میکنید. تصمیم میگیرید به دکتر مراجعه کنید. دکتر بعد از معاینات ابتدایی، چند آزمایش از شما میگیرد تا تشخیص دهد آیا یک بیماری نادر که تنها 1 نفر از هر 1000 نفر به آن مبتلا میشود در شما وجود دارد یا خیر. نتیجهی آزمایشات مثبت میشود و با نگرانی به مطب دکتر میروید تا مطمئن شوید نتیجه درست بوده است.
دکتر به شما میگوید که این آزمایش با میزان دقت 99% این بیماری را تشخیص میدهد. احتمال اینکه به این بیماری مبتلا باشید چقدر است؟ در نگاه اول به نظر میرسد که به احتمال خیلی بالا این بیماری را دارید؛ چون میزان دقت این آزمایش 99% بوده است. اما توماس بیز Thomas Bayes نظر دیگری دارد! توماس بیز یک آماردان و فیلسوف انگلیسی بود؛ بیشترین شهرت او مربوط به قضیهی (احتمالات) بیز است. طبق این قضیه، احتمال اینکه شما این بیماری را داشته باشید تنها 9% است.
قضیهی بیز احتمال وقوع یک رویداد را بر اساس دانش پیشین از شرایطی که ممکن است به آن رویداد مرتبط باشند، توصیف میکند. در این نوشتار میخواهیم قضیهی بیز را به بیان ساده و با استفاده از همان مثال بیماری توضیح دهیم.
احتمال شرطی
از آنجایی که نرخ این بیماری 1 در هزار نفر است، اگر 100 هزار نفر داشته باشیم، 100 نفر از آنها به این بیماری مبتلا خواهند بود و 99900 نفر دیگر آن را ندارند. اگر این 100 نفر آزمایش بدهند، 99 نفر جواب مثبت و 1 نفر جواب منفی میگیرند، چون میزان دقت آزمایش 99% است. اما این داستان جنبهی دیگری هم دارد که معمولاً نادیده گرفته میشود: اگر آن 99900 نفر این آزمایش را بدهند، جواب برای 1% یعنی 999 نفر از آنها مثبت کاذب خواهد بود.
حال اگر جواب آزمایش شما مثبت بوده، باید یکی از آن 99 نفری باشید که هم بیماری را دارند و هم جواب مثبت واقعی گرفتهاند. از طرفی، جمع تعداد افرادی که آزمایش را دادهاند و جواب مثبت گرفتهاند، 99+999 بوده است. پس احتمال اینکه شما واقعا این بیماری را داشته باشید، عبارت است از: ؛ یعنی احتمال 9% است. برای درک بهتر این موضوع از تصویر پایین کمک بگیرید.
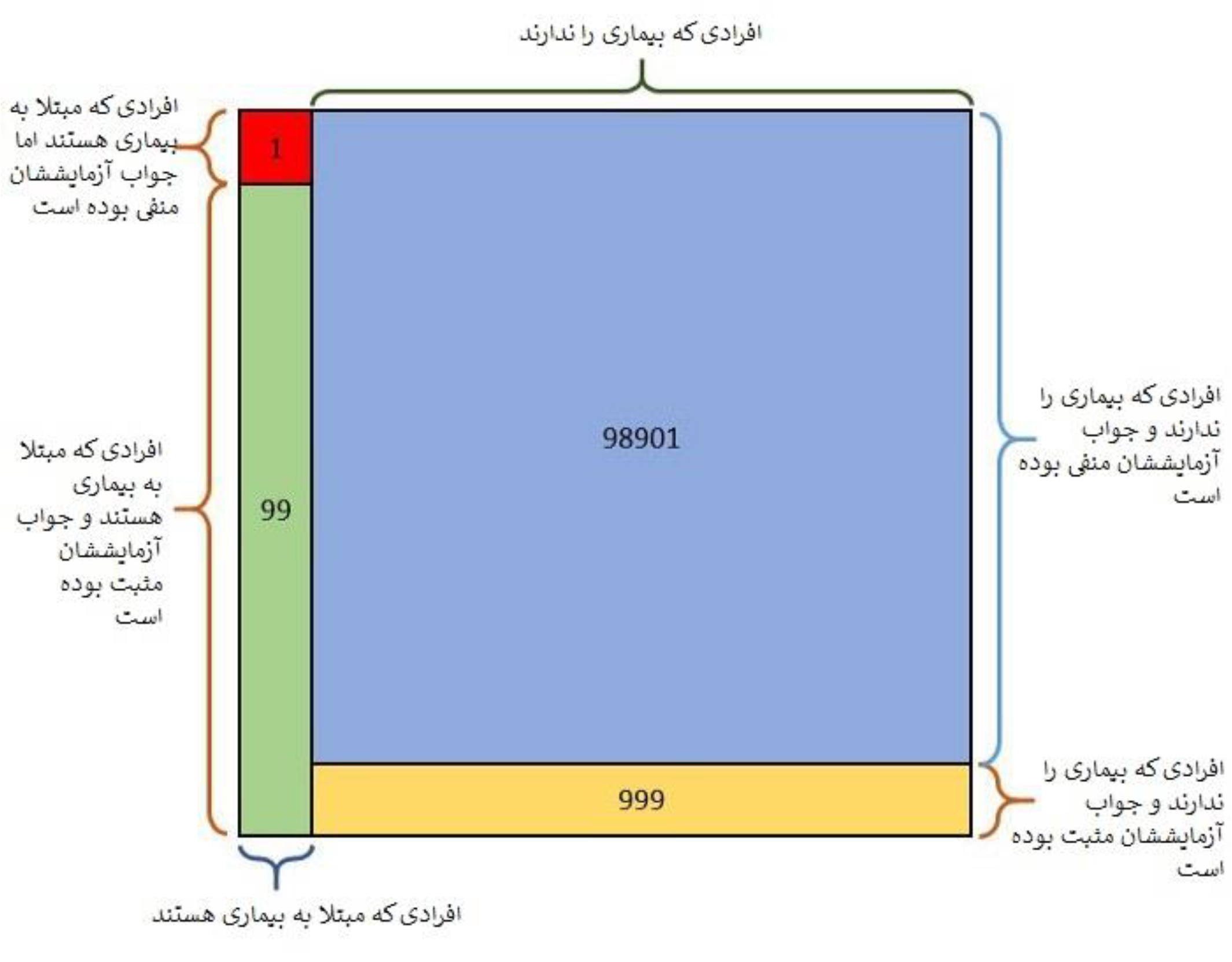
فرض میکنیم مربع بزرگ نشاندهندهی 100 هزار نفر (یا همان کل مجموعه) است. قسمت عمودی قرمزرنگ و سبزرنگی که در سمت چپ قرار دارند، آن 100 نفری هستند که بیماری را دارند. همانطور که میبینید این قسمت عمودی خود به دو ناحیه تقسیم میشود: قسمت سبزرنگ 99 نفری هستند که بیماری را دارند و جواب آزمایششان مثبت شده است، و قسمت قرمزرنگ که (با توجه به دقت 99 درصدی آزمایش) بیماری را دارند اما جواب منفی کاذب دریافت کردهاند.
به همین شکل، از 99900 نفری که به این بیماری مبتلا نیستند و آزمایش دادهاند، 999 نفر جواب مثبت کاذب گرفتهاند (قسمت زردرنگ) چون دقت آزمایش 99% است و 1% به درستی پیشبینی نمیشوند. حالا به خوبی متوجه میشوید که احتمال ابتلای شما به بیماری 9% یا است.
قضیهی بیز چارچوبی ارائه میدهد که مقدار احتمال یک فرضیه hypothesis (H) را در صورت وجود شواهد (E) محاسبه میکند. در مثال بالا، فرضیه ابتلای شما به بیماری و شواهد، نتیجهی آزمایش مثبت بود.
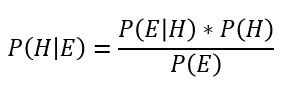
P(H|E : احتمال درست بودن فرضیه، در صورتی که شواهد درست باشد.
P(E|H): احتمال درست بودن شواهد، در صورتی که فرضیه درست باشد.
[irp posts=”19494″]ردهبند بیز ساده
ردهبند بیز ساده Naïve Bayes Classifier، همانطور که از اسمش مشخص است، از قانون بیز با مفروضههای ساده Naïve assumptions استفاده میکند.
ردهبندهای بیز ساده در بسیاری از مسائل ردهبندی متن و فیلتر ایمیلهای اسپم کاربرد دارند. فرض کنید میخواهیم یک ایمیل را در یکی از دو دستهی اسپم یا غیراسپم ردهبندی کنیم. از چند ویژگی ایمیل برای این ردهبندی استفاده میکنیم. بنابراین دیتاست آموزشی ما چیزی شبیه جدول پایین خواهد بود:
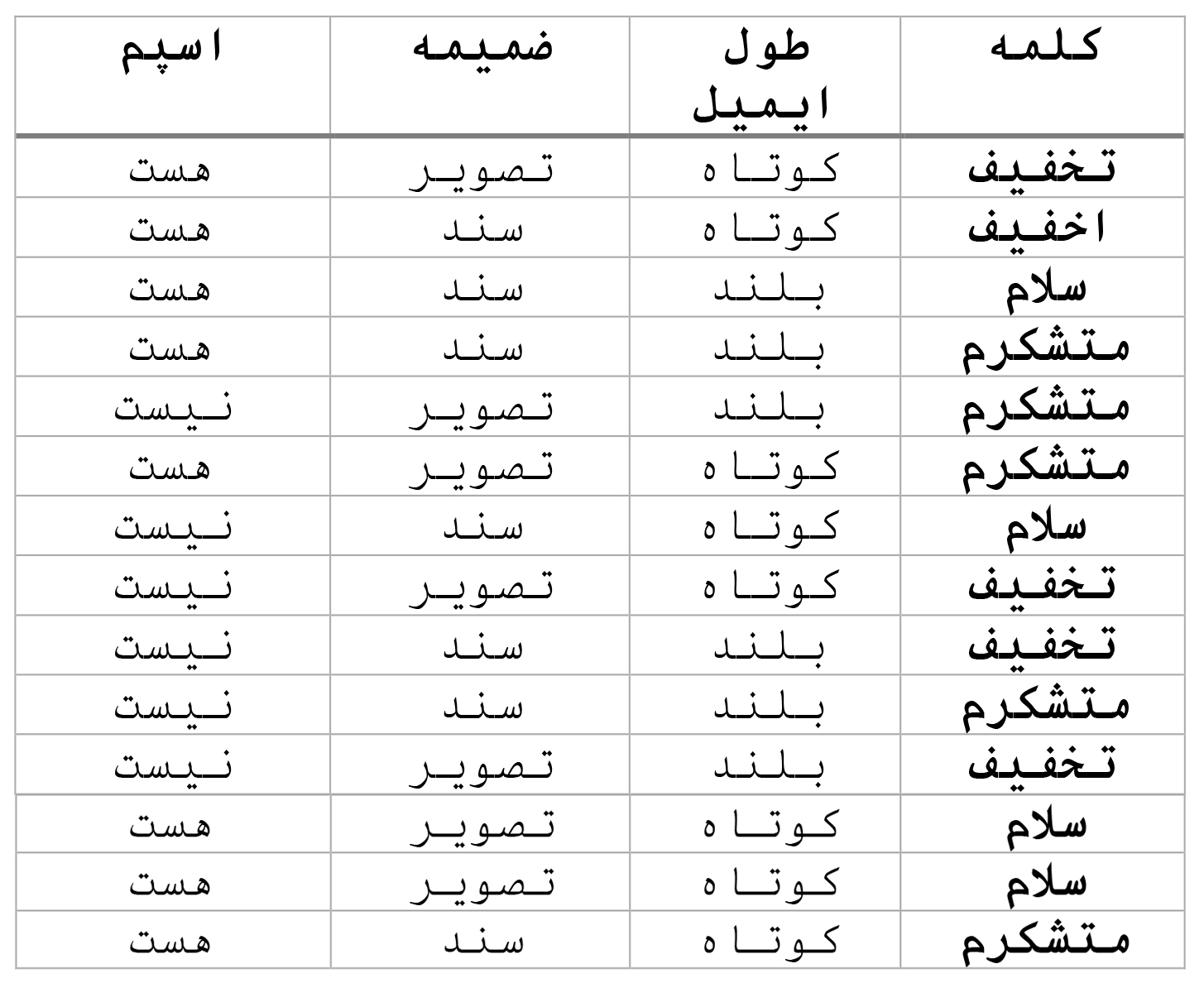
چند ویژگی دلخواه از ایمیل را انتخاب میکنیم، برای مثال آیا ایمیل کلمهی خاصی همچون تخفیف، سلام، یا متشکرم را دارد یا خیر، یا اینکه ایمیل کوتاه است یا بلند، آیا تصویر یا سندی به آن ضمیمه شده است یا خیر (این ویژگیها را فقط برای وضوح بیشتر و درک آسانتر مثال زدهایم؛ در واقعیت این ویژگیها با دقت بالایی انتخاب میشوند). به این ویژگیها، پیشبینی کننده نیز گفته میشود. مفروضههای ساده بدین قرارند:
- پیشبینی کننده ها یا ویژگیها از یکدیگر مستقل باشند. بدین معنی که هیچ همبستگی بین آنها (وجود کلمات مشخصشده، طول ایمیل یا نوع ضمیمه) وجود نداشته باشد. همهی سه ویژگی که در این مثال استفاده کردیم، باید به صورت مستقل اتفاق بیافتند.
- پیشبینی کننده ها در ردهبندی سهم برابری داشته باشند. یعنی هیچ ویژگی از دیگری مهمتر نباشد؛ به عبارتی وزن (ضریب اهمیت) آنها یکاندازه باشد.
در داده ها در دنیای واقعی، مفروضهی استقلال معمولاً هیچگاه برقرار نیست؛ با این حال، این الگوریتم در عمل به خوبی کار میکند.
به مثال ردهبندی ایمیل برمیگردیم، این مسئله را میتوانیم بدین شکل درآوریم:
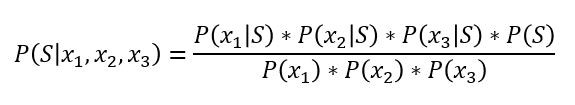
این فرمول، قانون بیز را با این مفروضه که همهی سه ویژگی مستقل باشند، نشان میدهد. حال این فرمول را تعمیم میدهیم:
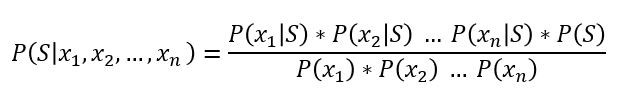
از آنجایی که P(S) برای مجموعهی آموزشی ما یک مقدار ثابت است و مخرج نیز یک مقدار ثابت است، فرمول بالا را میتوانیم بدین صورت درآوریم:
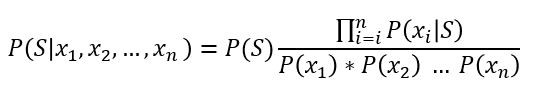
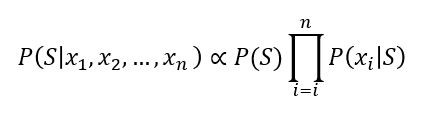
اگر بخواهیم مقادیر احتمال سمت راست جدول را به دست آوریم، احتمال وجود یک کلمه در صورت اسپم بودن ایمیل را محاسبه میکنیم. برای مثال، کلمهی تخفیف در کل 5 بار رخ داده است، 2 بار زمانی که ایمیل اسپم بوده و 3 بار زمانی که ایمیل اسپم نبوده است؛ پس میتوانیم بگوییم:
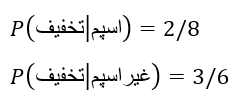
احتمالات دیگر را نیز میتوانیم به همین روش پیدا کنیم و آنها داخل معادله قرار دهیم. پس اگر یک ایمیل جدید داشته باشیم که طولانی است، یک تصویر به آن ضمیمه شده و کلمهی تخفیف هم در آن وجود دارد:

پاسخ معادلهی بالا 233/0 است؛ یعنی 33/23% احتمال دارد که ایمیل جدید اسپم باشد.
این اصل زیربنای مدل بیز ساده است. انواع مختلفی مدل بیز ساده برای ردهبندی وجود دارد: بیز ساده گاوسی Gaussian Naïve Bayes، بیز ساده چندجملهای Multinominal Naïve Bayes و بیز ساده برنولی Bernoulli Naïve Bayes. میتوانید در مورد این مدلها مطالعه کنید و ردهبند خود را بسازید. نکتهی مهم این است که ابتدا قضیهی بیز را به خوبی درک کنید تا بتوانید به درستی از آن استفاده کنید.

جمعبندی
بیز ساده یک الگوریتم ردهبندی پرسرعت است که درک و پیادهسازی آن آسان است و هزینهی محاسباتی کمی هم دارد. با وجود اینکه مفروضههایی قوی مبنی بر استقلال متغیرها (ویژگیها) دارد، در بسیاری از زمینهها به طور گسترده به کار میرود. پیشینه پژوهش و نمونههای اجرایی فراوانی از بیز ساده وجود دارد. همانطور که پیشتر گفتیم، درک کامل قضیهی احتمالات بیز، اساس پیادهسازی ردهبند بیز ساده است.





