
قسمت دوم از سری RL: یادگیری به کمک شبکه عمیق (DQN)
در این مقاله میخواهیم به کدنویسی DQN بپردازیم و یادگیری به کمک شبکه عمیق را مورد بررسی اساسی قرار دهیم.

عکس صفحه LunarLander-v0 از OpenAI Gym. جسم بنفش فضاپیمایی است که عامل RL باید کنترل آن را بیاموزد.
- پیادهسازی مربوطه در کتابخانهی PyTorch را میتوانید در این لینک Github مشاهده کنید.
- این نوشتار بخشی از یک مجموعهی چندقسمتی است؛ برای مطالعهی قسمت اول به این لینک مراجعه کنید.
LunarLander-v2 چیست؟
همانطور که در مقالهی قبلی توضیح داده شد، مسائل یادگیری تقویتی به عاملی نیاز دارند که با محیط تعامل برقرار میکند و اقداماتی بهینه انجام میدهد که او را به هدف میرسانند. LunarLander-v2 در جعبهابزار OpenAI gym نقش همان محیطی را دارد که یادگیری در آن رخ میدهد. شیء بنفشی که در تصویر بالا میبینید فضاپیمایی است که میخواهیم از طریق یادگیری تقویتی آن را کنترل کنیم؛ هدف از این مسئله، فرود آوردن فضاپیما روی صفحه فرود، یعنی فاصلهی بین دو پرچم زرد روی سطح ماه است.
برای اینکه بتوانیم این مسئله را به شکل نمودار بلوکی (شکل 1) مقالهی قبلی درآوریم، باید با مؤلفههای محیط LunarLander-v2 آشنا شویم (که در این کد قابل مشاهده هستند):
- حالت که به صورت برداری با 8 جزء نشان داده میشود: موقعیت افقی، موقعیت عمودی، سرعت افقی، سرعت عمودی، زاویه، سرعت زاویهای، (زمان) تماس پای چپ، تماس پای راست.
- در هر گام زمانی Time step، فضانورد میتواند یکی از چهار اقدام (no-op یا انجام هیچ کاری، روشن کردن موتور سمت چپ، روشن کردن موتور سمت راست، روشن کردن موتور وسط) را انتخاب کند.
- پاداش، که توسط محیط و بر اساس میزان سوخت استفاده شده، موقعیت فرود و زمان تماس پاها با سطح محاسبه میشود.
آمادهی سفر به ماه
قبل از هرچیز باید بدانیم چطور سفینه را برای فرودی ایمن آموزش دهیم. با اینکه DQN تقریباً منسوخ شده و جای خود را به الگوریتمهای پیچیدهتری داده، نقطهی شروع خوبی برای جستجو در دنیای یادگیری تقویتی عمیق به شمار میرود. شرکت DeepMind در مورد الگوریتم DQN که در سال 2015 به محبوبیت خوبی دست یافت، چنین میگوید: «DQN اولین مدل یادگیری عمیق است که توانسته با استفاده از یادگیری تقویتی، خطمشیهای کنترلی را مستقیماً از ورودیهای حسگر سطحبالا بیاموزد.» برای آشنایی بیشتر این ویدئو را تماشا کنید (در این ویدئو تلاش عامل DQN شرکت DeepMind را برای یادگیری بازی Breakout مشاهده میکنید).
نام این الگوریتم چیست؟
در این قسمت میخواهیم نام Deep Q Network را به اجزای آن تجزیه کنیم؛ Q به Q(s.a) اشاره دارد که به آن تابع اقدام-مقدار Action-value function گفته میشود. این تابع میزان خوب بودن یا کیفیت اجرای یک اقدام را در یک حالت خاص نشان میدهد. به بیان دیگر، تابع اقدام-مقدار به نتیجهای که انتظار میرود عامل با پیروی از خطمشی ، و بعد از اجرای اقدام a در حالت s به دست آورد، مقدار کمی میدهد. میخواهیم این توضیح را سادهتر کنیم و بیشتر وارد جزئیات آن شویم تا بفهمیم خطمشی و نتیجهی موردانتظار چه هستند؛ سپس به تعریف خود Q برمیگردیم.
خطمشی رفتاری است که عامل از خود به نمایش میگذارد. به بیان دیگر، عامل برای تصمیمگیری در مورد رفتاری که باید در حالت s از خود نشان دهد، از قانونی پیروی میکند که همان خطمشی است. خطمشی را اینطور نشان میدهند:

نتیجهی موردانتظار را میتوان جمع پاداشهای آینده دانست. مشکل این تعریف این است که، در واقعیت، انسانها ضریب یکسانی به پاداشهای کوتاهمدت و بلندمدت نمیدهند. برای مثال، شما این مطلب را میخوانید چون میدانید در بلندمدت برایتان مفید خواهد بود، اما در عین حال شاید دلتان بخواهد فیلمی تماشا کنید، که پاداش کوتاهمدت است؛ پس در چنین شرایطی باید به صورت منطقی تصمیم بگیرید میخواهید روی کدام پاداشها تمرکز کنید. اگر بخواهیم به این تصمیمگیری منطقی شکلی محاسباتی بدهیم، به معرفی ضریب کاهش Discounting factor (0 ≤ ? ≤ 1 ) میرسیم. بنابراین نتیجهی موردانتظار را میتوان بدین شکل نشان داد:

عامل به کمک ? تصمیم میگیرد باید روی چه چیزی تمرکز کند. شکل 1 بهتر میتواند ضریب کاهش را نشان دهد. وقتی مقدار ? نزدیک صفر باشد، عامل روی پاداشهای فوری تمرکز میکند و به همین دلیل در محیط LunarLander (خط نارنجی در نمودار پایین) نمرات کمتری به دست میآورد. اما وقتی مقدار ? به 1 نزدیکتر باشد (در مقالهی DQN روی 0/99 تنظیم شده) عامل دوربینترFar-sightedness شده و به نمرات بهتری میرسد.

حالا به تابع اقدام-مقدار یا همان Q در DQN برمیگردیم. تابع اقدام-مقدار، اندازهی نتیجهای را نشان میدهد که عامل انتظار دارد در حالت s با پیروی از خطمشی ? و انجام اقدام a به آن برسد:

این معادله را میتوان گسترش داد، به نحوی که تابع بهینهی اقدام-مقدارOptimal action-value function Q* را تعریف کند که در آن Q مقدار آغازین در حالت s است وقتی اقدام a با پیروی از خطمشی بهینه انجام میشود:

همانطور که مشاهده میکنید، خط سوم از معادلهی 4 شبیه به بخش داخل پرانتز خط دوم است، با این تفاوت که توالی r از r در گام زمانی t+1 شروع میشود. بنابراین قسمت داخل پرانتز میتواند نشاندهندهی مقدار تابع Q* برای جفت “حالت-اقدام” در گام زمانی t+1 باشد. هم تابع Q اقدام-مقدار و هم همتای بهینهی آن یعنی Q* امکان این ساختار بازگشتی Recursive formulation را مهیا میسازند. پس میتوان گفت تابع اقدام-مقدار جمع پاداش فوری و بهینهی کاهشی مقدار اقدام-مقدار در حالت موفق است. به این فرمولبندی (معادلهی 5) که از Q-مقدار تهیه شده معادلهی بلمن Bellman equation میگویند:

خب تا اینجا فهمیدیم Q در DQN به چه اشاره دارد؛ حال نوبت به DN یا شبکهی عمیق میرسد. DN به ما میگوید این تکنیک، همتای الگوریتم قدیمی یادگیری Q در یادگیری عمیق است. مزیت این تکنیک در کار با فضاهای بزرگی از حالت و اقدام است که محاسبه و ذخیرهی Q-مقدار برای هر جفت ممکن از حالت-اقدام در آنها کاری غیرممکن است. به همین دلیل، DQN از شبکههای عصبی استفاده میکند تا تابع بهینهی اقدام-مقدار (Q(s,a;?)≈Q*(s,a)) را برآورد کند. بنابراین وقتی یک جفت حالت-اقدام داشته باشیم، شبکهی عصبی که برای آن مسئله آموزش دیده میتواند مقدار تقریبی Q-مقدار بهینهی نهایی را به دست آورد.
شبکههای عصبی چطور میآموزند؟
در یادگیری نظارتشده، برای آموزش از دادهها استفاده میکنیم و یک مجموعه برچسب داریم که به شبکه دستورالعملهایی برای آموختن پاسخ درست ارائه میدهد. اینجا، در یادگیری تقویتی هم آموزش شبکهها از رویکردی مشابه پیروی میکند.

همانطور که در شکل بالا مشاهده میکنید، حالت کنونی s به عنوان ورودی وارد شبکه میشود؛ لایهی خروجی برای هر اقدام احتمالی که عامل میتواند در آن محیط خاص اجرا کند یک گره دارد. معماری شبکه (قسمت خاکستریرنگ) بسته به مسئلهای که میخواهید حل کنید میتواند ساده یا پیچیده باشد. گسترهی وسیعی از انواع شبکه وجود دارد که میتوانید از آنها استفاده کنید، شبکههای بسیار سادهی پیشرو FeedForward Neural Networks (FFNN) تا شبکههای عصبی پیچشی (CNN) یا شبکه های عصبی بازگشتی (RNN). برای این مجموعه ما از یک FFNN ساده استفاده کردیم که ورودی آن یک بردار 8 مؤلفهای است که حالت فضاپیما را در محیط توصیف میکند و خروجی آن 4 گره که هرکدام نمایندهی یکی از اقدامات ممکن هستند (که پیشتر توضیح دادیم).
حالا که میدانیم شبکه چیست و چه شکلی دارد، سؤال بعدی این است که چه تابع زیانی برای بهینهسازی پارامترهای شبکه استفاده میشود. اگر به تنظیمات و شرایط یادگیری نظارتشده نگاهی دوباره بیاندازیم، MSE (خطای میانگین مجذورات Mean Squared Error) برای یک نمونه اینطور نشان داده میشود: L=(target_y -predicted_y)². تابع زیان در یادگیری تقویتی نیز شکل مشابهی دارد. در این شرایط، predicted_y مقدار Q است که توسط شبکه در حالت s و با اقدام a محاسبه شده است. اما در یادگیری تقویتی برچسب نداریم، به همین خاطر از مفهوم خودراهاندازیBootstrapping استفاده میکنیم؛ به گفتهی ساتون و بارتو Sutton and Barto: «طی خودراهاندازی، برآوردهایی که از حالات انجام شده بر اساس برآوردهای مربوط به حالتهای موفق به روزرسانی میشوند.» به عبارت دیگر target_y نتیجهی فرمول بلمن از تابع اقدام-مقدار است. بنابراین تابع زیان برای هر نمونه را میتوان بدین شکل نشان داد: L=(targetQ-predictedQ)².
کدنویسی
حالا که همهی مؤلفههای لازم برای نوشتن کد را داریم، میدانیم شبکه باید چه شکلی داشته باشد، چگونه باید وزنهایش را بهروزرسانی کند و چطور باید با محیط تعامل برقرار کند. مشکل اینجاست که فرمولبندی سادهانگارانهای که بالاتر بیان کردیم منجر به آموزشی بیثبات میشود. برای مقابله با این مشکل مقالهای که DeepMind منتشر کرده دو راهکار مفید پیشنهاد میدهد:
- بافر بازپخشExperience Replay Buffer: زمانی که یادگیری مستقیماً از روی ترجکتوریها انجام میشود، بین نمونههای ورودی متوالی به صورت موقت همبستگی Correlation به وجود میآید. علاوه بر این، وقتی پارامترهای شبکه نمونهی بعدی را برای به روزرسانی وزنها تعیین میکنند، توزیع آموزش به شدت تغییر میکند. با این حال پیشفرض بیشتر نظریات یادگیری ماشینی محبوب و متداول این است که دادههای آموزشی باید مستقل بوده و توزیع یکسان داشته باشند. بنابراین الگوریتم DQN از بازپخش تجربه استفاده میکند تا این مفروضه را تایید کند.
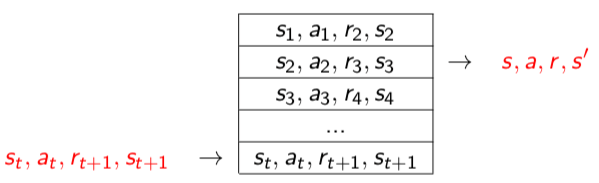
بافر بازپخش را یک دیتاست بزرگ در نظر بگیرید (همانند شکل 3) که زیرمجموعهای از تجارب پیشین عامل را دربرمیگیرد. در هر گام زمانی یک مجموعه 4 تایی (حالت، اقدام، پاداش، گام بعدی) که نشاندهندهی تجربهی عامل است به بافر بازپخش اضافه میشود. سپس برای به روز رسانی وزنها، یک بستهی کوچک از دادههای مربوط به تبدیلات تجربه به صورت یکسان (با وزن یکسان) از بافر بازپخش نمونهگیری میشوند و بدین ترتیب همبستگیهای زمانی قبلی را از بین میبرند.
علاوه بر اینها، از آنجایی که بافر بازپخش امکان استفادهی مجدد از نمونهها را فراهم میکند، هر مجموعه تجربه میتواند چندبار برای به روز رسانی وزنها مورد استفاده قرار گیرد. این امر منجر به افزایش کارآیی نمونه میشود، بدین معنی که تعداد نمونههای کمتری لازم است تا عامل مسئلهی مدنظر را بیاموزد.
- اهداف-Q ثابت: اگر به خاطر داشته باشید در بحث محاسبهی target_y در تابع زیان گفتیم برای به روزرسانی برآورد مقدار Q از برآورد مقادیر Q مربوط به حالات موفق استفاده میکنیم. این مسئله به یک چرخهی بازخوردی منتهی میشود. زیرا به روز رسانی وزنها که به خاطر تابع زیان خطا صورت گرفته، متعاقباً به مقدار برآوردشدهی Q منجر میشود که خود برای به روز رسانی target_y مورد استفاده قرار میگیرد و بدین طریق باعث میشود شبکه اهدافی غیرثابت را دنبال میکند.
بنابراین برای حل این مسئله، یک شبکه-Q دوم به نام شبکهی هدف معرفی میشود. معماری شبکهی هدف مشابه با معماری شبکهی موجود خطمشی است. تفاوت این دو شبکه در این است که شبکهی هدف ثابت میماند، ولی وزنهای شبکهی خطمشی در دورههای زمانی خاصی در شبکهی هدف کپی میشوند. بدین ترتیب، طی یادگیری، به سمت اهداف ثابتی حرکت میکنیم که با استفاده از شبکهی هدف برآورد شدهاند.
این دو تغییر و اصلاح شبکه باعث میشود مسئلهی یادگیری تقویتی به ساختار یادگیری نظارتشده که با آن آشنایی داریم نزدیکتر شود. بنابراین بافر بازپخش را میتوان به عنوان دیتاست آموزشی در نظر گرفت، و target_y شبکهی هدف نیز همانند برچسبها در ساختار یادگیری نظارتشده است. به همین ترتیب، تابع زیانی که برای آموزش استفاده میشود و از دو نسخهی شبکه استفاده میکند را میتوان بدین صورت نشان داد:

جمعبندی و مروری بر نحوهی تعامل همهی این اجزاء
حال همهی قطعات پازل را در دست داریم و میخواهیم بدانیم چطور کنار هم قرار میگیرند.

یکی از نکات مهم این نمودار مربوط به محاسبهی هدف-Q است. هر دادهای که در بستهی نمونهگیری شده از بافر بازپخش وجود دارد باید مورد بررسی قرار گیرد تا مشخص شود حالت نهایی است یا خیر. حالت نهایی حالتی است که در آن اپیزود کنونی done’ را به True مرتبط میکند. اگر دادهای نمایندهی یک حالت نهایی باشد، حالت دیگری بعد از آن وجود نخواهد داشت، بنابراین پاداشی از اقدامات بعدی انتظار نمیرود. در این شرایط، هدف-Q همان پاداش فوری خواهد بود که توسط عامل بعد از انجام اقدام a در حالت s دریافت شده است. از سوی دیگر اگر دادهای حالت نهایی نباشد، طبق معادلهی بلمن (معادله 5) علاوه بر اینکه آن را پاداش فوری در نظر میگیریم، در مورد اقداماتی که عامل ممکن است در آینده انجام دهد نیز اطلاعاتی دریافت میکنیم.
کدنویسی
تا حد زیادی میتوان گفت همین گردش کار را در کدنویسی پیاده میکنیم. شکل 4 پیادهسازی الگوریتم DQN را به صورت دقیق نشان میدهد. هایپرپارامترهای لازم برای تنظیم الگوریتم و مقادیری که من در اجراهای محیط LunarLander استفاده کردم عبارتاند از:
- ظرفیت بافر بازپخش Capacity of replay buffer = 3000 (معمولاً کمتر از 10⁶ نگه داشته میشود)؛
- بستهداده کوچک از تبدیلاتMini-batch of transitions نمونهگیری شده از بافر بازپخش= 64 (معمولاً 32 یا 64 در نظر گرفته میشود)؛
- اندازهی شروع بازپخش، N= 1000 (از این پارامتر قبل از شروع یادگیری، برای افزایش حافظهی بازپخش با استفاده از یک خطمشی تصادفی استفاده میشود)؛
- حداکثر تعداد اپیزودها= 3000
- اپسیلون = 0/05 (در این مقاله این مقدار را ثابت در نظر گرفتهایم اما در مقالهی بعدی بیشتر به آن خواهیم پرداخت)؛
- ضریب کاهش، ?= 0/99.
- معماری شبکه= شبکهی عصبی پیشخور با یک لایهی ورودی شامل 8 گره، دو لایهی نهان با 256 گره در هرکدام، و یک لایهی خروجی با 4 گره؛ از الگوریتم Adam نیز با مقادیر پیشفرض خودش به عنوان بهینهساز استفاده کردم.
نتیجهی آموزش با این هایپرپارامترها را در شکل پایین مشاهده میکنید:

گام بعدی
امیدواریم به کمک این مطلب با نحوهی کار DQN آشنا شده باشید. در این صورت، حال نوبت شماست که این الگوریتم را با استفاده از این گردشکار پیادهسازی کنید.
شما میتوانید کد مربوط به عامل DQN برای تولید این نمودارها را در این مقاله از Github دانلود کنید. همچنین اگر اولین بار است که با Gym کار میکنید، این مطالب میتوانند برایتان مفید باشد.
اگر وقت دارید و میخواهید درک عمیقتری از این الگوریتم به دست آورید پیشنهاد میکنم به این مطالب هم سری بزنید:
- Human-level control : مقالهی اصلی که دو اصلاحیه معرفی شده توسط DeepMind را توضیح میدهد.
- DeepRL Bootcamp 2017: Deep Q-Networks: یک ویدئوی یک ساعته از یکی از نویسندگان مقالهی DQN






