انتخاب تابع زیان مناسب برای آموزش شبکه‌های عصبی یادگیری عمیق

برای آموزش شبکه‌های عصبی یادگیری عمیق، از الگوریتم بهینه‌سازی گرادیان  نزولی تصادفی استفاده می‌شود. برآورد مکرر خطای مدل یکی از مراحل الگوریتم بهینه‌سازی است. بدین منظور باید یک تابع خطا یا تابع زیان انتخاب کرد. وزن‌های مدل بر اساس زیان برآوردشده توسط این تابع، به روزرسانی می‌شوند و بدین طریق در دور بعدی آموزش، زیان مدل را کاهش می‌دهند.

مدل‌های شبکه‌ی عصبی بر اساس نمونه‌های آموزشی یاد می‌گیرند چطور ورودی‌ را به خروجی  نگاشت کنند.‌ هر مدل پیش‌بینی، هدف خاصی (برای مثال رگرسیون یا رده‌بندی) دارد و تابع زیان باید متناسب با این هدف انتخاب شود. تنظیمات لایه‌ی خروجی نیز باید با تابع زیان انتخاب‌شده مطابقت داشته باشد.

در این مقاله با نحوه‌ی انتخاب تابع زیان برای انواع مسائلی که شبکه‌های عصبی عمیق حل می‌کنند، آشنا خواهیم شد.

انتظار می‌رود پس از مطالعه‌ی این نوشتار، بتوانید:

• در مسائل رگرسیون، مدل را برای تابع زیان خطای میانگین مجذورات تنظیم کنید؛
• در مسائل رده‌بندی دودویی، مدل را برای توابع زیان آنتروپی متقاطع و hinge تنظیم کنید؛
• در مسائل رده‌بندی چندکلاسه، مدل برای توابع زیان آنتروپی متقاطع و واگرایی KL تنظیم کنید.

در این نوشتار، روی معرفی و پیاده‌سازی انواع توابع زیان تمرکز خواهیم کرد.

برای کسب اطلاعات بیشتر در مورد مبنای نظری توابع زیان، به این مقاله مراجعه کنید.

توابع زیان رگرسیون

هدف از مسائل رگرسیون، پیش‌بینی متغیری با مقدار حقیقی می‌باشد.

در این قسمت در مورد توابع زیانی صحبت خواهیم کرد که مناسب مسائل رگرسیون هستند.

بدین منظور از یک تابع مولد استاندارد  رگرسیون استفاده می‌کنیم که در کتابخانه‌ی Scikit-Learn، با تابع make_regression() function  فراخوانی می‌شود. خروجی این تابع، مسائل رگرسیون ساده‌ای هستند که متغیرهای ورودی، نویز آماری و سایر خواص لازم را دارند.

با استفاده از این تابع، مسئله‌ای با 20 ویژگی ورودی تولید می‌کنیم؛ به طوری که 10 مورد از این ویژگی‌ها معنادار بوده و 10 مورد دیگر غیرمعنادار باشند. در کل، 1000 نمونه به صورت تصادفی تولید می‌شوند. مولد شبه‌تصادفی را به نحوی تنظیم می‌کنیم که مطمئن شویم در هربار اجرای کد، همان 1000 نمونه را می‌گیریم:

# generate regression dataset
X, y = make_regression(n_samples=1000, n_features=20, noise=0.1, random_state=1)

هنگامی که متغیرهای ورودی و خروجی با مقادیر حقیقی در یک بازه‌ی منطقی و قابل قبول مقیاس‌بندی شده باشند، شبکه‌های عصبی عموماً عملکرد بهتری از خود نشان می‌دهند. از آن‌جایی که در این مسئله، همه‌ی متغیرهای ورودی و هدف توزیع گاوسی دارند، بهتر است داده‌ها را استانداردسازی کنیم.

بدین منظور می‌توانیم از کلاس  StandardScaler از کتابخانه‌ی Scikit-Learn استفاده کنیم. در مسائل واقعی، ابتدا باید مقیاس‌بند را روی دیتاست آموزشی تعریف و سپس روی مجموعه‌های آموزشی و آزمایشی مستقل اجرا کنیم؛ اما اینجا برای آسان‌سازی مطالب، قبل از تقسیم داده‌ها به مجموعه‌های آموزشی و آزمایشی، عملیات مقیاس‌بندی را روی همه‌ی آن‌ها اجرا می‌کنیم:

# standardize dataset
X = StandardScaler().fit_transform(X)
y = StandardScaler().fit_transform(y.reshape(len(y),1))[:,0]

بعد از مقیاس‌بندی، داده‌ها به صورت مساوی در دو دسته‌ی آموزشی و آزمایشی تقسیم می‌شوند:

برای حل این مسئله‌ی رگرسیون و معرفی انواع توابع زیان، از یک مدل کوچک پرسپترون چندلایه‌ای (MLP) استفاده می‌کنیم.

# split into train and test
n_train = 500
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]

با توجه به مسئله‌ی تعریف شده، مدل 20 ویژگی به عنوان ورودی می‌پذیرد، یک لایه‌ی نهان با 25 گره داشته و از تابع فعالسازی ReLU (یا خطی یکسوسازی‌شده) استفاده می‌کند. از آن‌جایی که خروجی باید یک عدد حقیقی باشد، لایه‌ی خروجی مدل یک گره داشته و از تابع فعالسازی خطی استفاده می‌کند.

# define model
model = Sequential()
model.add(Dense(25, input_dim=20, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(1, activation='linear'))

مدل با گرادیان کاهشی تصادفی، نرخ یادگیری 01/0 و ممنتوم 9/0 (هر دو مقادیر پیش‌فرض قابل‌قبولی هستند) آموزش خواهد دید.

تعداد دورهای آموزشی 100 است. در انتهای هر دور، مدل روی دیتاست آزمایشی ارزیابی شده و منحنی یادگیری آن رسم می‌گردد:

opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss='...', optimizer=opt)
# fit model
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=100, verbose=0)

حال که مسئله و مدل پایه را در دست داریم، می‌توانیم سه تابع زیانی که برای مسائل رگرسیون مناسب هستند را بررسی کنیم.

با این‌که مدل به کاررفته در این قسمت MLP است، این توابع زیان را در آموزش CNNها و RNNها نیز (برای رگرسیون) می‌توان به کار برد.

تابع زیان خطای میانگین مجذورات

تابع زیان پیش‌فرض در مسائل رگرسیون، خطای میانگین مجذورات یا MSE می‌باشد.

از نظر ریاضیاتی، در صورتی که از «چارچوب استنباطی برآورد بیشینه‌سازی» استفاده کنیم و متغیر هدف، توزیع گاوسی داشته باشد، اولویت با استفاده از تابع MSE است. این تابع زیان را باید ابتدا ارزیابی کرد و تنها در شرایط خاص، با دلیل موجه، تغییر داد.

تابع MSE میانگین مجذورات تفاوت‌های بین مقادیر حقیقی و پیش‌بینی شده را محاسبه می‌کند. فارغ از علامت مقادیر حقیقی و پیش‌بینی شده، مقدار MSE همیشه مثبت یا صفر خواهد بود. مجذور گرفتن از مقدار تفاوت‌ها باعث می‌شود اشتباهات بزرگ‌تر در مقایسه با اشتباهات کوچک‌تر، خطای بیشتری دریافت کنند؛ بدین معنی که مدل برای اشتباهات بزرگش جریمه می‌شود.

برای استفاده از تابع MSE در کتابخانه‌ی Keras، mse یا mean_squared_error را هنگام کامپایل مدل به عنوان تابع زیان تعریف می‌کنیم:

model.compile(loss='mean_squared_error')

بهتر است لایه‌ی خروجی، یک گره (برای یک متغیر هدف) داشته باشد و از تابع فعالسازی خطی استفاده کند:

model.add(Dense(1, activation='linear'))

کد پایین اجرای کامل MLP را در مسئله‌ی رگرسیون مذکور نشان می‌دهد:

# mlp for regression with mse loss function
from sklearn.datasets import make_regression
from sklearn.preprocessing import StandardScaler
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import SGD
from matplotlib import pyplot
# generate regression dataset

با اجرای این کد، ابتدا تابع MSE مدل روی دیتاست‌های آموزشی و آزمایشی پرینت می‌شود.

نکته: با توجه به ذات تصادفی الگوریتم، فرآیند ارزیابی و یا تفاوت‌های موجود در دقت عددی، امکان این وجود دارد که نتایج شما با اعدادی که در این مقاله مشاهده می‌کنید تفاوت داشته باشند. برای رفع این مشکل، می‌توانید کد بالا را چندین بار تکرار کرده و میانگین خروجی‌ها را به دست آورید.

در نتیجه‌ی اجرای کد بالا، مشاهده می‌کنیم خطای آموزش مدل (تا سه رقم اعشار) صفر است:

Train: 0.000, Test: 0.001

علاوه بر این، یک نمودار خطی هم به دست می‌آوریم که زیان MSE را بر حسب دورهای آموزشی برای مجموعه‌ی آموزشی (آبی‌رنگ) و آزمایشی (نارنجی‌رنگ) نشان می‌دهد.

با توجه به نمودار، می‌توان گفت مدل با سرعت قابل قبولی به سوی مقدار بهینه همگرا شده است. عملکرد مدل روی دیتاست‌های آموزشی و آزمایشی تقریباً برابر است. عملکرد مدل و نحوه‌ی همگرایی آن نشان می‌دهد که MSE برای شبکه‌ی عصبی که این مسئله را آموخته، گزینه‌ی خوبی بوده است.

تابع زیان میانگین مجذورات لگاریتمی

در برخی از مسائل رگرسیون، مقادیر متغیر هدف در بازه‌ای گسترده قرار می‌گیرند؛ هنگام پیش‌بینی مقادیر بزرگ، بهتر است مدل را به اندازه‌ای که در MSE تنبیه می‌شد، جریمه نکنیم.

در این صورت، ابتدا لگاریتم طبیعی(   مقادیر پیش‌بینی شده را به دست آورده و سپس خطای میانگین مجذورات را محاسبه می‌کنیم. به این تابع زیان، خطای میانگین مجذورات لگاریتمی یا MSLE گفته می‌شود.

MSLE، بر خلاف MSE، در خطاهای بزرگ اثر تبیهی آرام تری در نظر می گیرد.

اگر قرار باشد مدل مستقیماً مقادیری  مقیاس‌بندی نشده را پیش‌بینی کند، MLSE معیار بهتری برای اندازه‌گیری زیان خواهد بود. در این قسمت، با استفاده از همان مسئله‌ی رگرسیون ساده، این تابع زیان را توضیح می‌دهیم.

بدین منظور مدل قبلی  با استفاده از تابع زیان mean_squared_logarithmic_error  به روزرسانی میشود و در عین حال، همان تنظیمات قبلی(تنظیمات بخش MSE) را در لایه‌ی خروجی نگه  داشته میشود. با این حال، هنگام برازش مدل، MSE را هم محاسبه می‌کنیم تا بتوانیم از آن به عنوان معیار ارزیابی عملکرد مدل   استفاده کرده و منحنی یادگیری مدل را رسم کنیم.

model.compile(loss='mean_squared_logarithmic_error', optimizer=opt, metrics=['mse'])

کد پایین، استفاده از تابع زیان MSLE را به صورت کامل نشان می‌دهد:

# mlp for regression with msle loss function
from sklearn.datasets import make_regression
from sklearn.preprocessing import StandardScaler
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import SGD
from matplotlib import pyplot
# generate regression dataset

با اجرای کد بالا، ابتدا MSE مدل روی مجموعه‌های آموزشی و آزمایشی پرینت می‌شود.

نکته: با توجه به ذات تصادفی الگوریتم، فرآیند ارزیابی و یا تفاوت‌های موجود در دقت عددی، امکان این وجود دارد که نتایج شما با اعدادی که در این مقاله مشاهده می‌کنید تفاوت داشته باشند. برای رفع این مشکل، می‌توانید کد بالا را چندین بار تکرار کرده و میانگین خروجی‌ها را محاسبه کنید.

اینجا مشاهده می‌کنیم که MSE مدل در هر دو دیتاست آموزشی و آزمایشی نتایج ضعیف‌تری را نشان می‌دهد. بنابراین با توجه به این‌که توزیع متغیر هدف گاوسی است، MSE گزینه‌ی چندان مناسبی برای این مسئله به شمار نمی‌رود:

Train: 0.165, Test: 0.184

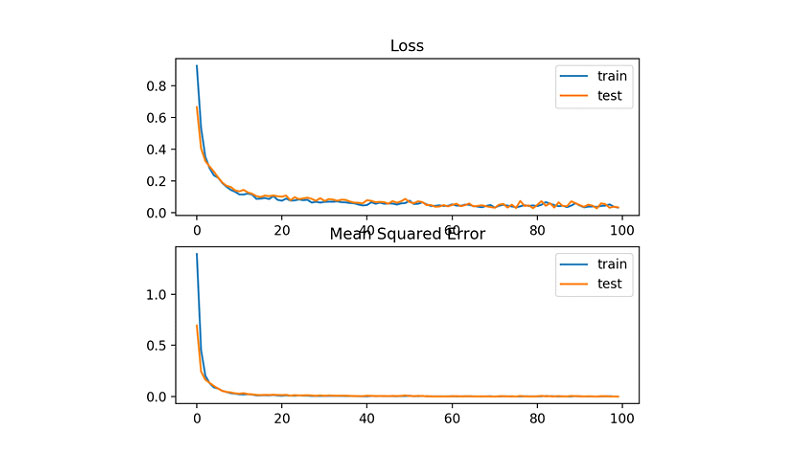
یک نمودار خطی نیز ترسیم می‌شود که زیان MLSE را بر حسب دورهای آموزشی، برای مجموعه‌ی آموزشی (آبی‌رنگ) و آزمایشی (نارنجی‌رنگ) نمایش می‌دهد؛ نمودار پایین همین مقادیر را برای زیان MSE نشان می‌دهد.

همانطور که در این نمودار مشاهده می‌کنید، در طول این 100 دور، MLSE همگرایی خوبی داشته است. اما به نظر می‌رسد MSE علائمی از بیش‌برازش نشان می‌دهد؛ زیرا به سرعت افت کرده و از حدود دور 20 به بعد شروع به افزایش می‌کند.

تابع زیان میانگین قدرمطلق خطا

در برخی از مسائل رگرسیون، توزیع متغیر هدف گاوسی است، اما مقادیر پرت هم دارد. منظور از مقادیر پرت، مقادیر خیلی کوچک یا خیلی بزرگی هستند که از میانگین فاصله دارند.

در این موارد، میانگین قدرمطلق خطا (MAE) گزینه‌ی مناسبی به شمار می‌رود، چون نسبت به مقادیر پرت مقاوم است. این تابع، میانگین قدرمطلق تفاوت‌های بین مقادیر حقیقی و پیش‌بینی‌شده را محاسبه می‌کند.

با به روزرسانی مدل می‌توانیم از تابع زیان mean_absolute_error استفاده کرده و تنظیمات قبلی را برای لایه‌ی خروجی نگه داریم:

model.compile(loss='mean_absolute_error', optimizer=opt, metrics=['mse'])

کد پایین، استفاده از تابع زیان میانگین قدرمطلق خطا در یک مسئله‌ی رگرسیون را به صورت کامل نمایش می‌دهد:

# mlp for regression with mae loss function
from sklearn.datasets import make_regression
from sklearn.preprocessing import StandardScaler
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import SGD
from matplotlib import pyplot
# generate regression dataset

با اجرای این کد، ابتدا خطای میانگین مجذورات(MSE) مدل روی دیتاست‌های آموزشی و آزمایشی پرینت می‌شود.

نکته: با توجه به ذات تصادفی الگوریتم، فرآیند ارزیابی و یا تفاوت‌های موجود در دقت عددی، امکان این وجود دارد که نتایج شما با اعدادی که در این مقاله مشاهده می‌کنید تفاوت داشته باشند. برای رفع این مشکل، می‌توانید کد بالا را چندین بار تکرار کرده و میانگین خروجی‌ها را محاسبه کنید.

در این مثال، خطای مدل (تا سه رقم اعشار) برابر با صفر است:

Train: 0.002, Test: 0.002

علاوه بر این، نمودار خطی تابع زیان MAE (بر حسب دورهای آموزشی) نیز رسم می‌شود. در این نمودار، زیان مدل روی مجموعه‌ی آموزشی با رنگ آبی و روی مجموعه‌ی آزمایشی با رنگ نارنجی مشخص شده است. نمودار پایینی همین مقادیر را برای خطای MSE نشان می‌دهد.

با توجه به نمودار مشاهده می‌کنیم که MAE پس از طی مسیری پر از نوسان، همگرا می‌شود. این در حالی است که MSE چنین نوساناتی از خود نشان نمی‌دهد. همانطور که می‌دانیم، توزیع گاوسی متغیر هدف، استاندارد است و هیچ مقدار پرتی ندارد؛ به همین دلیل MAE گزینه‌ی مناسبی برای این مدل به شمار نمی‌رود.

احتمالاً اگر متغیر هدف را در ابتدای کار مقیاس‌بندی نکنیم، به نتایج بهتری دست یابیم.

توابع زیان برای مسائل رده‌بندی دودویی

مسائل رده‌بندی دودویی مسائلی هستند که در آن‌ها از دو برچسب موجود، فقط یکی می‌تواند به نمونه‌ها اختصاص داده شود.

این مسائل اغلب به صورت پیش‌بینی مقدار 0 یا 1 (یکی از دو کلاس) برای نمونه‌ها صورت‌بندی می‌شوند. پیاده‌سازی آن‌ها هم معمولاً به صورت پیش‌بینی احتمال تعلق هر نمونه به کلاس 1 انجام می‌شود.

در این قسمت، توابع زیانی را با هم بررسی می‌کنیم که برای مسائل رده‌بندی دودویی مناسب هستند.

بدین منظور از مسئله‌ی آزمایشی دایره‌ها در Scikit-Learn استفاده می‌کنیم. «مسئله‌ی دایره‌ها» شامل دو دایره‌ی متحدالمرکز می‌شود که در یک فضای دوبُعدی قرار دارند؛ نقاط دایره‌ی بیرونی (بزرگ‌تر) متعلق به کلاس 0 و نقاط دایره‌ی داخلی مربوط به کلاس 1 هستند. با افزودن نویز آماری به نمونه‎‌ها، ابهام افزایش یافته و یادگیری مسئله برای مدل چالش‌برانگیزتر می‌شود.

در این مثال، 1000 نمونه تولید کرده و 10% نویز آماری اضافه می‌کنیم. مولد شبه‌تصادفی را به نحوی تنظیم می‌کنیم که مطمئن شویم همیشه همان 1000 نمونه را می‌گیریم:

# generate circles
X, y = make_circles(n_samples=1000, noise=0.1, random_state=1)

برای درک مسئله‌ای که می‌خواهیم مدلسازی کنیم می‌توانیم یک نمودار پراکندگی نیز رسم کنیم. کد کامل بدین شکل است:

# scatter plot of the circles dataset with points colored by class
from sklearn.datasets import make_circles
from numpy import where
from matplotlib import pyplot
# generate circles
X, y = make_circles(n_samples=1000, noise=0.1, random_state=1)
# select indices of points with each class label
for i in range(2):

با اجرای این کد، نمودار پراکندگی نمونه‌ها را نیز ترسیم می‌کنیم. در این نمودار، ورودی‌ها همان موقعیت نقاط هستند و رنگ نقاط توسط مقدار کلاس تعیین می‌شود (کلاس 0 با رنگ آبی و کلاس 1 با رنگ نارنجی مشخص می‌شود).

همانطور که مشاهده می‌کنید، نقاط به خوبی اطراف 0 مقیاس‌بندی شده و تقریباً همگی در بازه‌ی [-1,1] قرار گرفته‌اند. به همین دلیل نیازی به مقیاس‌بندی مجدد آن‌ها نیست.

دیتاست به صورت مساوی به مجموعه‌های آموزشی و آزمایشی تقسیم می‌شود:

# split into train and test
n_train = 500
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]

برای حل این مسئله می‌توان یک مدل ساده MLP تعریف کرد. این مدل دو ورودی برای دو ویژگی موجود در دیتاست، یک لایه‌ی نهان با 50 گره، تابع فعالسازی ReLU و یک لایه‌ی خروجی دارد که باید متناسب با تابع زیان انتخاب شده تنظیم گردد:

# define model
model = Sequential()
model.add(Dense(50, input_dim=2, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(1, activation='...'))

opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss='...', optimizer=opt, metrics=['accuracy'])

مدل با استفاده از گرادیان کاهشی تصادفی، با نرخ یادگیری که به صورت پیش‌فرض مقدار قابل قبولی (01/0) دارد و ممنتوم 9/0 آموزش می‌بیند.

مدل را طی 200 دور آموزش می‌دهیم. در انتهای هر دور، دقت و زیان مدل را ارزیابی می‌کنیم تا منحنی‌های یادگیری آن را رسم کنیم:

# fit model
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=200, verbose=0)

اکنون که مسئله و مدل پایه را در دست داریم، به معرفی سه تابع زیانی می‌پردازیم که در مسائل رده‌بندی دودویی عملکرد خوبی دارند.

با این‌که در این مثال‌ها از MLP استفاده می‌کنیم، توابع زیانی که توضیح خواهیم داد در CNNها و RNNها هم کاربرد خواهند داشت.

تابع زیان آنتروپی متقاطع دودویی

تابع زیان پیش‌فرض مسائل رده‌بندی دودویی، آنتروپی متقاطع است.

این تابع زیان برای کاربرد در مسائل رده‌بندی دودویی ساخته شده است که در آن‌ها، مقدار هدف در مجموعه‌ی {0, 1} قرار می‌گیرد.

از نظر ریاضیاتی، اگر از «چارچوب استنباطی برآورد بیشینه‌سازی» استفاده کنیم، اولویت با تابع زیان آنتروپی متقاطع است. این تابع زیان را باید ابتدا ارزیابی کرد و تنها در صورتی تغییر داد که دلیل موجهی وجود داشته باشد.

تابع آنتروپی متقاطع، میانگین تفاوت‌های بین توزیع‌های واقعی و پیش‌بینی‌شده‌ی احتمال (یعنی احتمال تعلق نمونه به کلاس 1) را  محاسبه می‌کند. سپس مقدار به دست آمده به حداقل می‌رسد. مقدار ایده‌آل آنتروپی متقاطع 0 است.

برای اجرای آنتروپی متقاطع در کتابخانه‌ی Keras، می‌توان هنگام کامپایل مدل، binary_crossentropy را به عنوان تابع زیان تعریف کرد:

model.compile(loss='binary_crossentropy', optimizer=opt, metrics=['accuracy'])

برای اجرای این تابع، لایه‌ی خروجی باید یک گره داشته و تابع فعالسازی آن سیگموئید باشد تا احتمال تعلق همه‌ی نمونه‌ها به کلاس 1  را پیش‌بینی کند:

model.add(Dense(1, activation='sigmoid'))

کد زیر اجرای کامل مدل MLP روی یک مسئله‌ی رده‌بندی دودویی دو دایره‌ای را نشان می‌دهد:

# mlp for the circles problem with cross entropy loss
from sklearn.datasets import make_circles
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import SGD
from matplotlib import pyplot
# generate 2d classification dataset
X, y = make_circles(n_samples=1000, noise=0.1, random_state=1)

با اجرای این کد، ابتدا دقت رده‌بندی مدل روی دیتاست‌های آموزشی و آزمایشی پرینت می‌شود.

نکته: با توجه به ذات تصادفی الگوریتم، فرآیند ارزیابی و یا تفاوت‌های موجود در دقت عددی، امکان این وجود دارد که نتایج شما با اعدادی که در این مقاله مشاهده می‌کنید تفاوت داشته باشند. برای رفع این مشکل، می‌توانید کد بالا را چندین بار تکرار کرده و میانگین خروجی‌ها را محاسبه کنید.

همانطور که مشاهده می‌کنید، مدل یادگیری قابل قبولی داشته و به دقت حدود 83% روی دیتاست آموزشی و حدود 85% روی دیتاست آزمایشی دست یافته است. نزدیکی این مقادیر به هم نزدیک حاکی از عدم بیش‌برازش و کم‌برازش مدل است:

Train: 0.836, Test: 0.852

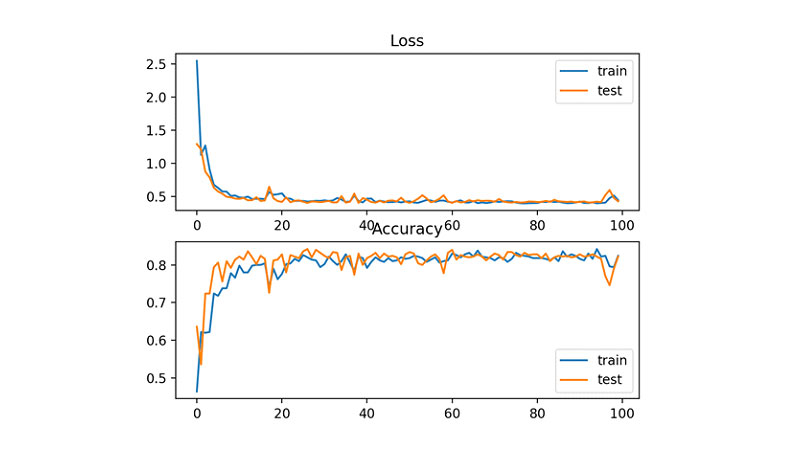
کد بالا علاوه بر دقت مدل، دو نمودار خطی هم تولید می‌کند؛ نمودار بالایی، زیان آنتروپی متقاطع را روی مجموعه‌های آموزشی (آبی‌رنگ) و آزمایشی (نارنجی‌رنگ) نشان می‌دهد و نمودار پایینی، دقت رده‌بندی مدل (بر حسب دورهای آموزشی) را نشان می‌دهد.

بر مبنای این نمودارها می‌توان نتیجه گرفت که فرآیند آموزش، همگرایی خوبی داشته است. با توجه به ذات پیوسته‌ی خطا در توزیع‌های احتمال، نمودار مربوط به زیان تقریباً صاف و بدون نوسان است. اما نمودار دقت نوسانات زیادی دارد، چون نمونه‌های موجود در مجموعه‌های آموزشی و آزمایشی صرفاً به صورت صحیح/غلط پیش‌بینی می‌شوند. به همین دلیل بازخوردی که از عملکرد مدل ارائه می‌شود، جزئیات کمتری دارد.

زیان Hinge

در مسائل رده‌بندیی دودویی می‌توان به جای آنتروپی متقاطع، از تابع زیان Hinge استفاده کرد؛ این تابع زیان در اصل برای استفاده در مدل‌های ماشین بردار پشتیبان (SVM) طراحی شده است.

در یک مسئله‌ی رده‌بندی دودویی که مقادیر هدف در مجموعه‌ی {-1, 1} قرار می‌گیرند، می‌توان این تابع را به کار برد.

تابع زیان Hinge، وقتی بین مقادیر واقعی و پیش‌بینی شده تفاوت وجود داشته باشد، خطای بیشتری محاسبه می‌کند؛ بدین طریق به اختصاص برچسب درست به نمونه‌ها کمک می‌کند.

بین گزارشاتی که از عملکرد تابع زیان Hinge ارائه شده‌‌اند، توافق نظری وجود ندارد. به طور کلی می‌توان گفت برخی اوقات در مسائل رده‌بندی دودویی، این تابع عملکرد بهتری نسبت به آنتروپی متقاطع دارد.

در ابتدا، متغیر هدف باید اصلاح (مقیاس‌بندی) شود تا مقادیر آن در مجموعه‌ی {-1, 1} قرار گیرند:

# change y from {0,1} to {-1,1}
y[where(y == 0)] = -1

سپس می‌توان تابع زیان Hinge را به صورت ‘hinge‘ در تابع کامپایل تعریف کرد:

در آخر، لایه‌ی خروجی شبکه باید به نحوی تنظیم شود که یک گره‌ی واحد داشته باشد. تابع فعالسازی این لایه باید تانژانت هایپربولیک باشد تا بتواند یک مقدار واحد در بازه‌ی [-1, 1] را به عنوان خروجی تولید کند:

model.compile(loss='hinge', optimizer=opt, metrics=['accuracy'])

کد زیر، اجرای مدل MLP با تابع زیان hinge را در یک مسئله‌ی رده‌بندی دودویی به صورت کامل نشان می‌دهد:

model.add(Dense(1, activation='tanh'))

در نتیجه‌ی اجرای کد بالا، ابتدا دقت رده‌بندی مدل روی مجموعه‌های آموزشی و آزمایشی پرینت می‌شود.

# mlp for the circles problem with hinge loss
from sklearn.datasets import make_circles
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import SGD
from matplotlib import pyplot
from numpy import where
# generate 2d classification dataset

نکته: با توجه به ذات تصادفی الگوریتم، فرآیند ارزیابی و یا تفاوت‌های موجود در دقت عددی، امکان این وجود دارد که نتایج شما با اعدادی که در این مقاله مشاهده می‌کنید تفاوت داشته باشند. برای رفع این مشکل، می‌توانید کد بالا را چندین بار تکرار کرده و میانگین خروجی‌ها را محاسبه کنید.

اگر نتایج به دست آمده را با نتایج آنتروپی متقاطع مقایسه کنیم، متوجه افت نسبی عملکرد مدل خواهیم شد؛ به نحوی که دقت آن روی مجموعه‌های آموزشی و آزمایشی به کمتر از 80% می‌رسد:

Train: 0.792, Test: 0.740

کد بالا، علاوه بر دقت مدل، تصویری حاوی دو نمودار نیز تولید می‌کند. نمودار بالایی، تابع Hinge را بر حسب دورهای آموزشی، برای دیتاست‌های آموزشی (آبی‌رنگ) و آزمایشی (نارنجی‌رنگ)، نشان می‌دهد. نمودار پایینی هم دقت رده‌بندی مدل را بر حسب دورهای آموزشی نشان می‌دهد.

نمودار مربوط به زیان Hinge نشان می‌دهد مدل همگرا شده و روی هر دو مجموعه عملکرد قابل قبولی داشته است. نمودار دقت نیز همگرایی داشته، اما انتظار می‌رفت مسیر همگرایی آن نوسانات کمتری داشته باشد.

زیان مجذور Hinge

تابع زیان Hinge نسخه‌های گوناگون فراوانی دارد که اغلب در مدل‌های SVM به کار می‌روند.

یکی از نسخه‌های این تابع، مجذور Hinge نام دارد که مجذور نمره‌ی تابع زیان Hinge را محاسبه می‌کند. در نتیجه‌ی به جذر رساندن این مقدار، سطح تابع خطا هموارتر (بدون نوسان) شده و بدین ترتیب اجرای عملیات‌های عددی روی آن آسان‌تر می‌شود.

اگر استفاده از تابع زیان Hinge در یک مسئله‌ی رده‌بندی دودویی منجر به عملکردی خوب شود، احتمالاً تابع زیان مجذور Hinge هم گزینه‌ی خوبی برای آن مسئله خواهد بود.

برای استفاده از زیان مجذور Hinge نیز مانند زیان Hinge، باید متغیر هدف را مقیاس‌بندی کرد تا در بازه‌ی {-1, 1} قرار گیرد:

# change y from {0,1} to {-1,1}
y[where(y == 0)] = -1

تابع زیان مجذور Hinge را می‌توان هنگام تعریف مدل، به عنوان squared_hinge در تابع compile() تعریف کرد:

model.compile(loss='squared_hinge', optimizer=opt, metrics=['accuracy'])

لایه‌ی خروجی باید یک گره‌ی واحد داشته باشد و از تابع فعالسازی تانژانت هایپربولیک استفاده کند تا خروجی، مقادیری پیوسته در بازه‌ی [-1, 1] باشند:

model.add(Dense(1, activation='tanh'))

کد پایین اجرای مدل MLP با تابع زیان مجذور Hinge را در یک مسئله‌ی رده‌بندی دودویی نشان می‌دهد:

# mlp for the circles problem with squared hinge loss
from sklearn.datasets import make_circles
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import SGD
from matplotlib import pyplot
from numpy import where
# generate 2d classification dataset

با اجرای این کد، ابتدا دقت رده‌بندی مدل را روی دیتاست‌های آموزشی و آزمایشی به دست می‌آوریم.

نکته: با توجه به ذات تصادفی الگوریتم، فرآیند ارزیابی و یا تفاوت‌های موجود در دقت عددی، امکان این وجود دارد که نتایج شما با اعدادی که در این مقاله مشاهده می‌کنید تفاوت داشته باشند. برای رفع این مشکل، می‌توانید کد بالا را چندین بار تکرار کرده و میانگین خروجی‌ها را محاسبه کنید.

همانطور که مشاهده می‌کنید، در این مسئله و با این تنظیمات مدل، تابع زیان مجذور Hinge گزینه‌ی مناسبی به شمار نمی‌رود و دقت رده‌بندی مدل روی مجموعه‌های آموزشی و آزمایشی را به کمتر از 70% کاهش می‌دهد:

Train: 0.682, Test: 0.646

کد بالا علاوه بر دقت مدل، تصویری حاوی دو نمودار خطی نیز تولید می‌کند. نمودار بالایی، زیان مجذور Hinge را بر حسب دورهای آموزشی، برای مجموعه‌های آموزشی (آبی‌رنگ) و آزمایشی (نارنجی‌رنگ) نشان می‌دهد و نمودار پایینی دقت رده‌بندی مدل را به نمایش می‌گذارد.

با توجه به نمودار تابع زیان متوجه همگرایی مدل خواهیم شد، اما سطح تابع خطا به اندازه‌ی سایر توابع خطایی که تا اینجا دیدیم، هموار نیست؛ به نحوی که تغییرات کوچک در وزن‌ها منجر به تغییراتی شدید در تابع زیان می‌شوند.

توابع زیان مسائل رده‌بندی چندکلاسه

منظور از رده‌بندی چندکلاسه، مسائل پیش‌بینی هستند که در آن‌ها، نمونه‌ها به بیش از دو کلاس اختصاص می‌یابند.

این مسائل اغلب در قالب پیش‌بینی یک عدد صحیح صورت‌بندی می‌شوند، به صورتی که به هر کلاس، یک عدد صحیح از 0 تا num_classes – 1 اختصصاص داده می‌شود. این مسائل، احتمال تعلق نمونه‌ها به هر کدام از این کلاس‌ها را پیش‌بینی می‌کنند.

در این قسمت، توابع زیانی را بررسی می‌کنیم که برای کاربرد در مسائل مدلسازی پیش‌بینی رده‌بندی چندکلاسه، گزینه‌ مناسبی به شمار می‌روند.

بدین منظور از مسئله‌ی blobs استفاده می‌کنیم. با استفاده از تابع make_blobs() function  کتابخانه‌ی Scikit-learn، می‌توانیم مسائل رده‌بندی چندکلاسه با تعداد کلاس‌ها و ویژگی‌های ورودی مشخصی تولید کنیم. اینجا یک مسئله‌ی رده‌بندی سه کلاسه، با دو متغیر ورودی و 1000 نمونه تولید می‌کنیم. مولد شبه تصادفی به نحوی تنظیم می‌شود که در هر بار اجرای کد، همان 1000 نمونه را به دست بدهد:

# generate dataset
X, y = make_blobs(n_samples=1000, centers=3, n_features=2, cluster_std=2, random_state=2)

متغیرهای ورودی می‌توانند مختصات x و y نقاط روی یک صفحه‌ی دو بُعدی باشند.

با اجرای کد پایین، یک نمودار پراکندگی از کل دیتاست به دست می‌آوریم. در این نمودار، رنگ نقاط بر اساس کلاسی که به آن تعلق دارند مشخص می‌شود.

# scatter plot of blobs dataset
from sklearn.datasets import make_blobs
from numpy import where
from matplotlib import pyplot
# generate dataset
X, y = make_blobs(n_samples=1000, centers=3, n_features=2, cluster_std=2, random_state=2)
# select indices of points with each class label
for i in range(3):

در نمودار پراکندگی به دست آمده از 1000 نمونه‌ی موجود در دیتاست، نمونه‌های متعلق به کلاس‌های 0، 1 و 2 به ترتیب با رنگ‌های آبی، نارنجی، و سبز مشخص می‌شوند:

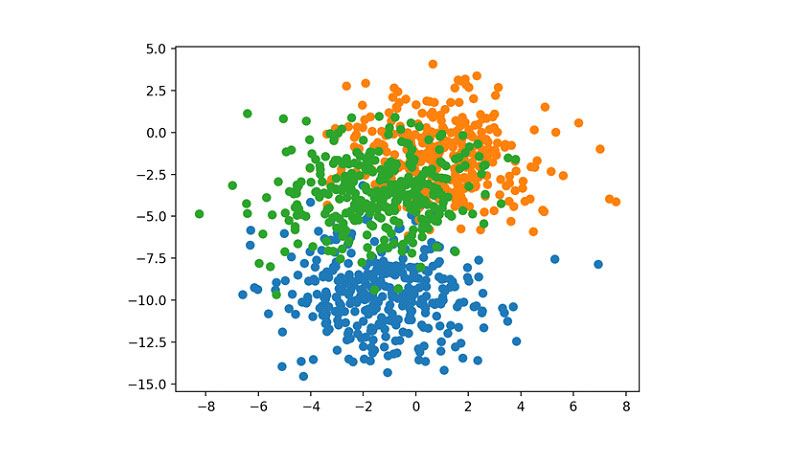
# split into train and test
n_train = 500
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]

ویژگی‌های ورودی، توزیع گاوسی دارند و به همین دلیل امکان استانداردسازی آن‌ها وجود دارد. با این حال، برای اختصار مطلب، اینجا مقیاس‌بندی اجرا نمی‌کنیم.

دیتاست به صورت برابر به دو مجموعه‌ی آموزشی و آزمایشی تقسیم می‌شود:

# split into train and test
n_train = 500
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]

برای بررسی توابع زیان، از یک مدل MLP کوچک استفاده می‌کنیم.

ورودی این مدل، دو متغیر است؛ در لایه‌ی نهان آن 50 گره وجود دارد و تابع فعالسازی آن ReLU است. لایه‌ی خروجی این مدل باید بر اساس تابع زیان انتخابی تنظیم شود:

# define model
model = Sequential()
model.add(Dense(50, input_dim=2, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(..., activation='...'))

این مدل با استفاده از گرادیان کاهشی، با نرخ یادگیری پیش‌فرض (01/0) و ممنتوم 9/0 آموزش می‌بیند:

# compile model
opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss='...', optimizer=opt, metrics=['accuracy'])

آموزش مدل طی 100 دور انجام می‌شود. برای ارزیابی تابع زیان مدل و دقت رده‌بندی آن روی مجموعه‌های آموزشی و آزمایشی، در انتهای هر دور، مدل را روی دیتاست آزمایشی اجرا و منحنی‌های یادگیری آن را رسم می‌کنیم:

# fit model
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=100, verbose=0)

حال که مدل و مسئله‌ی پایه را در دست داریم، می‌توانیم سه تابع زیانی که در مسائل رده‌بندی چندکلاسه به کار می‌روند را توضیح دهیم.

با این‌که برای توضیح این سه تابع زیان از MLP استفاده می‌کنیم، این توابع را روی CNNها و RNNها (در مسائل رده‌بندی چندکلاسه) نیز می‌توان به کار برد.

تابع زیان آنتروپی متقاطع چندکلاسه

تابع زیان پیش‌فرض در مسائل رده‌بندی چندکلاسه، تابع آنتروپی متقاطع است.

این تابع در مسائل رده‌بندی چندکلاسه‌ای به کار می‌رود که در آن‌ها مقادیر در مجموعه‌ی {0, 1, 3, …, n} قرار می‌گیرند و به هر کلاس یک مقدار (عدد صحیح) مشخص اختصاص داده می‌شود.

آنتروپی متقاطع، میانگین تفاوت‌های بین توزیع واقعی و توزیع پیش‌بینی شده‌ی احتمال (برای همه‌ی کلاس‌های موجود) را محاسبه می‌کند. این نمره کمینه‌سازی می‌شود. مقدار ایده‌آل آنتروپی متقاطع 0 است.

برای اجرای آنتروپی متقاطع در کتابخانه‌ی Keras، می‌توان categorical_crossentropy را هنگام کامپایل مدل تعریف کرد:

model.compile(loss='categorical_crossentropy', optimizer=opt, metrics=['accuracy'])

برای استفاده از این تابع، لایه‌ی خروجی باید به نحوی تنظیم شود که n گره (یک گره برای هر کلاس) داشته باشد (پس در این مسئله، سه گره خواهیم داشت). تابع فعالسازی لایه‌ی خروجی باید Softmax باشد تا مقدار احتمال برای همه‌ی کلاس‌ها پیش‌بینی شود:

model.add(Dense(3, activation='softmax'))

بنابراین می‌توان گفت متغیر هدف باید به صورت one-hot کدگذاری شده باشد.

هدف این است که احتمال تعلق همه‌ی نمونه‌ها به کلاس واقعی برابر با 0/1 و احتمال تعلق آن‌ها به کلاس‌های دیگر برابر با 0/0 باشد. بدین منظور می‌توانیم از تابع to_categorical() Keras function  استفاده کنیم:

# one hot encode output variable
y = to_categorical(y)

کد زیر، اجرای مدل MLP روی مسئله‌ی رده‌بندی چندکلاسه blobs را به صورت کامل نشان می‌دهد:

# mlp for the blobs multi-class classification problem with cross-entropy loss
from sklearn.datasets import make_blobs
from keras.layers import Dense
from keras.models import Sequential
from keras.optimizers import SGD
from keras.utils import to_categorical
from matplotlib import pyplot
# generate 2d classification dataset

با اجرای این نمونه، دقت رده‌بندی مدل روی دیتاست‌های آموزشی و آزمایشی را به دست می‌آوریم.

نکته: با توجه به ذات تصادفی الگوریتم، فرآیند ارزیابی و یا تفاوت‌های موجود در دقت عددی، امکان این وجود دارد که نتایج شما با اعدادی که در این مقاله مشاهده می‌کنید تفاوت داشته باشند. برای رفع این مشکل، می‌توانید کد بالا را چندین بار تکرار کرده و میانگین خروجی‌ها را محاسبه کنید.

همانطور که مشاهده می‌کنید، مدل عملکرد خوبی داشته و دقت رده‌بندی آن روی دیتاست آموزشی چیزی حدود 84% و روی دیتاست آزمایشی حدود 82% است:

Train: 0.840, Test: 0.822

کد بالا، علاوه بر میزان دقت مدل، دو نمودار هم تولید می‌کند. نمودار بالایی تابع زیان آنتروپی متقاطع را بر حسب دورها، برای مجموعه‌ی آموزشی (آبی‌رنگ) و آزمایشی (نارنجی‌رنگ) نشان می‌دهد. نمودار پایینی هم نشان‌دهنده‌ی دقت رده‌بندی مدل است.

نمودار حاکی از همگرایی مدل به سمت مقدار بهینه است. نمودارهای زیان و دقت هردو همگرایی داشته‌اند، البته نوسانات نسبتاً زیادی دارند. با توجه به این‌که علائمی از بیش‌برازش یا کم‌برازش دیده نمی‌شود، می‌توان نتیجه گرفت که تنظیمات مدل خوب بوده است. با تنظیم نرخ یادگیری یا اندازه‌ی بسته‌داده‌ها می‌توان مسیر همگرایی را هموارتر کرد.

تابع زیان آنتروپی متقاطع چندکلاسه Sparse

اگر بخواهیم در مسائلی از آنتروپی متقاطع استفاده کنیم که برچسب‌های زیادی دارند، عواملی از جمله رمزگذاری One-hot می‌توانند چالش‌برانگیز باشند.

برای مثال، در مسئله‌ی پیش‌بینی کلمات مناسب (برای جایگذاری در یک جمله)، دیتاست ممکن است ده‌ها یا صدها هزار دسته داشته باشد که هر کدام برچسب خود را دارند. در این صورت، مؤلفه‌های هدف (برای همه‌ی نمونه‌های آموزشی) به برداری نیاز دارند که به روش One-hot رمزگذاری شده باشد؛ در این صورت ده‌ها و صدها هزار صفر و یک خواهیم داشت که حافظه‌ی بسیار زیادی اشغال می‌کنند.

آنتروپی متقاطع Sparse برای رفع این مشکل معرفی شده است. این تابع، خطا را مانند آنتروپی متقاطع محاسبه می‌کند، اما برای استفاده از آن لازم نیست متغیر هدف قبل از آموزش به صورت one-hot رمزگذاری شده باشد.

برای استفاده از آنتروپی متقاطع Sparse در مسائل رده‌بندی چندکلاسه در Keras، می‌توان  sparse_categorical_crossentropy را در تابع compile() تعریف کرد:

model.compile(loss='sparse_categorical_crossentropy', optimizer=opt, metrics=['accuracy'])

برای پیاده‌سازی این تابع، لایه‌ی خروجی باید به نحوی تنظیم شود که n گره، یعنی برای هرکلاس یک گره، داشته باشد (در این مثال 3 گره). علاوه بر این، تابع فعالسازی لایه‌ی خروجی باید softmax باشد تا بتواند احتمال تعلق نمونه‌ها به همه‌ی کلاس‌ها را پیش‌بینی کند:

model.add(Dense(3, activation='softmax'))

همانطور که گفته شد، مزیت این تابع در این است که نیازی به رمزگذاری One-hot متغیر هدف ندارد.

کد زیر، پیاده‌سازی کامل مدل MLP با تابع زیان آنتروپی متقاطع Sparse را در یک مسئله‌ی رده‌بندی چندکلاسه blobs نشان می‌دهد:

# mlp for the blobs multi-class classification problem with sparse cross-entropy loss
from sklearn.datasets import make_blobs
from keras.layers import Dense
from keras.models import Sequential
from keras.optimizers import SGD
from matplotlib import pyplot
# generate 2d classification dataset
X, y = make_blobs(n_samples=1000, centers=3, n_features=2, cluster_std=2, random_state=2)
# split into train and test
n_train = 500
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]
# define model
model = Sequential()
model.add(Dense(50, input_dim=2, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(3, activation='softmax'))
# compile model
opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss='sparse_categorical_crossentropy', optimizer=opt, metrics=['accuracy'])
# fit model
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=100, verbose=0)
# evaluate the model
_, train_acc = model.evaluate(trainX, trainy, verbose=0)
_, test_acc = model.evaluate(testX, testy, verbose=0)
print('Train: %.3f, Test: %.3f' % (train_acc, test_acc))
# plot loss during training
pyplot.subplot(211)
pyplot.title('Loss')
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='test')
pyplot.legend()
# plot accuracy during training
pyplot.subplot(212)
pyplot.title('Accuracy')
pyplot.plot(history.history['accuracy'], label='train')
pyplot.plot(history.history['val_accuracy'], label='test')
pyplot.legend()
pyplot.show()

با اجرای این کد، دقت رده‌بندی مدل روی دیتاست‌های آموزشی و آزمایشی را به دست می‌آوریم

نکته: با توجه به ذات تصادفی الگوریتم، فرآیند ارزیابی و یا تفاوت‌های موجود در دقت عددی، امکان این وجود دارد که نتایج شما با اعدادی که در این مقاله مشاهده می‌کنید تفاوت داشته باشند. برای رفع این مشکل، می‌توانید کد بالا را چندین بار تکرار کرده و میانگین خروجی‌ها را محاسبه کنید.

با توجه به اعداد به دست آمده می‌توان گفت مدل عملکرد خوبی داشته است. اگر این آزمایش را به دفعات زیاد تکرار کنیم، میانگین عملکرد آنتروپی متقاطع معمولی و sparse تقریباً برابر با هم خواهد بود:

Train: 0.832, Test: 0.818

کد بالا علاوه بر دقت مدل، دو نمودار خطی نیز تولید می‌کند. نمودار بالایی، آنتروپی متقاطع Sparse را بر حسب دورهای آموزشی، روی دیتاست‌های آموزشی (آبی‌رنگ) و آزمایشی (نارنجی‌رنگ) نشان می‌دهد. نمودار پایینی هم دقت رده‌بندی مدل را نشان می‌دهد.

با توجه به نمودارهای زیان و دقت می‌توان گفت در طول آموزش، مدل به خوبی به سوی مقدار بهینه همگرا شده است

تابع زیان واگرایی کولبک لیبلر

تابع زیان واگرایی کولبک لیبلر یا واگرایی KL معیاری است برای اندازه‌گیری تفاوت بین توزیع احتمال و توزیع  پایه.

اگر مقدار زیان واگرایی KL صفر باشد، توزیع‌ها مشابه هم هستند. در عمل رفتار واگرایی KL شباهت زیادی به آنتروپی متقاطع دارد. این تابع نشان می‌دهد اگر برای برآورد متغیر هدف از توزیع احتمال پیش‌بینی شده استفاده شود، چه میزان اطلاعات (به واحد بیت) از دست خواهد رفت.

به همین دلیل، واگرایی KL را بیشتر در مدل‌هایی به کار می‌برند که صرفاً رده‌بندی چندکلاسه انجام نمی‌دهند، بلکه تابع پیچیده‌تری را برآورد می‌کنند؛ به عنوان مثال می‌توان به خودرمزنگارهایی اشاره کرد که برای بازآفرینی ورودی اصلی، بازنمایی متراکمی از ویژگی‌ها را می‌آموزند. در چنین شرایطی، اولویت با تابع واگرایی KL است؛ با این حال، برای رده‌بندی چندکلاسه هم می‌توان از این تابع زیان استفاده کرد. عملکرد تابع واگرایی KL در این دست مسائل، برابر با عملکرد تابع آنتروپی متقاطع است.

برای پیاده‌سازی واگرایی KL در کتابخانه‌ی Keras، می‌توان kullback_leibler_divergence را در تابع compile() تعریف کرد:

model.compile(loss='kullback_leibler_divergence', optimizer=opt, metrics=['accuracy'])

مانند آنتروپی متقاطع، اینجا هم لایه‌ی خروجی باید n گره (برای هر کلاس، یک گره) داشته باشد و تابع فعالسازی آن softmax باشد تا احتمال هر کلاس را پیش‌بینی کند.

شباهت دیگر این تابع با آنتروپی متقاطع این است که متغیر هدف باید به صورت One-hot رمزگذاری شده باشد تا مقدار احتمال تعلق نمونه به کلاس واقعی 0/1 و به سایر کلاس‌ها 0/0 باشد:

# one hot encode output variable
y = to_categorical(y)

کد زیر، اجرای مدل MLP با تابع زیان واگرایی KL را در یک مسئله‌ی رده‌بندی چندکلاسه blobs نشان می‌دهد:

# mlp for the blobs multi-class classification problem with kl divergence loss
from sklearn.datasets import make_blobs
from keras.layers import Dense
from keras.models import Sequential
from keras.optimizers import SGD
from keras.utils import to_categorical
from matplotlib import pyplot
# generate 2d classification dataset

با اجرای این کد، دقت رده‌بندی مدل روی دیتاست‌های آموزشی و آزمایشی را به دست می‌آوریم.

نکته: با توجه به ذات تصادفی الگوریتم، فرآیند ارزیابی و یا تفاوت‌های موجود در دقت عددی، امکان این وجود دارد که نتایج شما با اعدادی که در این مقاله مشاهده می‌کنید تفاوت داشته باشند. برای رفع این مشکل، می‌توانید کد بالا را چندین بار تکرار کرده و میانگین خروجی‌ها را محاسبه کنید.

همانطور که مشاهده می‌کنید، عملکرد این تابع شبیه به نتایج آنتروپی متقاطع است:

Train: 0.822, Test: 0.822

علاوه بر دقت مدل، دو نمودار خطی نیز تولید می‌شوند؛ نمودار بالایی واگرایی KL روی دیتاست‌های آموزشی (آبی‌رنگ) و آزمایشی (نارنجی‌رنگ) را بر حسب دورهای آموزشی نشان می‌دهد. نمودار پایینی هم نمایشگر دقت رده‌بندی مدل است.

با توجه به این نمودارها می‌توان نتیجه گرفت که همگرایی هم در تابع زیان و هم در دقت رده‌بندی خوب بوده است. با توجه به شباهت مقادیر به دست آمده، احتمال این که آنتروپی متقاطع نیز به نتایج مشابهی دست یابد، زیاد است.

جمع‌بندی

در این مطلب آموزشی، آموختیم چطور برای شبکه‌های عصبی یادگیری عمیق، توابع زیانی متناسب با مسئله‌ی مدلسازی پیش‌بین انتخاب کنیم.

به بیان دقیق‌تر، دریافتیم:

• چطور در مسائل رگرسیون، مدل را با تابع زیان خطای میانگین مجذورات و مشتقات آن تنظیم کنیم.
• چطور در مسائل رده‌بندی دودویی، مدل را با آنتروپی متقاطع و زیان Hinge تنظیم کنیم.
• چطور در مسائل رده‌بندی چندکلاسه، مدل را با آنتروپی متقاطع و واگرایی KL تنظیم کنیم.