
فراتر از شبکههای پیچشی گراف
هرچند اصطلاح شبکههای عصبی گراف (GNN) Graph Neural Networks (GNNs) (نسبتاً جدید است اما با بهرهگیری از رویکرد یادگیری عمیق در تجزیه و تحلیل گرافها مورد استفاده قرار میگیرد و در این مسیر توانسته محبوبیت زیادی پیدا کند. از آنجاییکه GNNها به طور طبیعی توانایی سازگاری با دیتاست های دنیای واقعی ، که دارای ساختار گرافی هستند، را دارند، در حوزههای مختلفی از جمله تبلیغات اینترنتی، پیشبینی ترافیک جاده، طراحی دارو و غیره مورد استفاده قرار میگیرند. در پست کاربردهای شبکههای عصبی گراف فهرستی از حوزههایی ارائه شده که GNN ها توانستهاند در آنها عملکرد چشمگیری داشته باشند.
نمونههای اولیه GNN ها اطلاعات همسایه را منتشر میکردند و تا زمانی که به یک نقطه ثابت دست پیدا کنند این کار را ادامه میدادند و از این طریق میتوانستند نمایش گره مقصد Target node’s representation را یاد بگیرند. GNNها به سرعت پیشرفت کردند و از سایر رویکردهای موفق یادگیری عمیق برای ارتقای معماری خود که امروزه با نام شبکههای پیچشی گراف (GCN) Graph Convolution Networks (GCN) شناخته میشود، استفاده کردند.
شبکههای پیچشی گراف
همانگونه که از نام آن بر میآید شبکههای پیچشی گراف بر پایه شبکههای عصبی پیچشی Convolution Neural Networks
شکل گرفتهاند و دوباره آنها را برای گرافها تعریف میکنند. هدف چارچوبهای پیچشی این است که همانند تصاویر، اطلاعات همسایه را برای نودهای گراف نیز ذخیره کنند.

GCNها به دو دسته GCNهای طیفی Spectral GCNs و GCNهای فضایی Spatial GCNs تقسیمبندی میشوند. GCNهای طیفی پیچشهای گراف را با پیش زمینه پردازش سیگنال گراف که مبتنی بر تئوری طیفی گراف است، تعریف میکنند.
از منظر پردازش سیگنال گراف که بر پایه نظریه طیفی گراف Graph spectral theory شکل گرفته فیلترهایی معرفی میکنند و از این طریق پیچشهای گراف گوناگونی ارائه میدهند. در مقابل شبکههای پیچشی گراف فضایی از طریق جمعآوری اطلاعات ویژگیهای همسایهها، پیچشهای گراف را ارائه میدهند. یکی از نقاط ضعف رویکرد طیفی این است که در این رویکرد کل گراف باید به صورت همزمان پردازش شود که در گرافهای بزرگی همچون گرافهای شبکه اجتماعی که از میلیونها گره و لبه تشکیل شده این کار غیر ممکن است. یکی دیگر از نقاط ضعف رویکردهای طیفی که ریشه در همین پردازش همزمان کل شبکه دارد این است که در این روش بهرهگیری از پردازش موازی Parallel processing دشوار است. شبکههای پیچشی گراف فضایی این مشکل را ندارند چرا که آنها با جمعآوری اطلاعات گره همسایه، پیچش را به صورت مستقیم در دامنه گراف اجرا میکنند. محاسبه به همراه استراتژیهای نمونهبرداری را میتوان به جای اینکه در کل گراف اجرا کرد، در دستهای از گرهها اجرا کرد که قابلیت افزایش کارایی را دارد.
یکی دیگر از نقاط ضعف شبکههای پیچشی گراف طیفی این است که برای یک گراف ثابت و مشخص طراحی شدهاند و تعمیم آنها به گرافهای جدید و متفاوت دشوار است. در مقابل مدلهای فضایی پیچش گراف را به صورت محلی بر روی هر یک از گرهها اجرا میکنند و به همین دلیل میتوانند به سادگی وزنها را میان محلها و ساختارهای گوناگون تقسیم کنند. طی سالهای اخیر به دلایلی که گفته شد، مدلهای فضایی توانستهاند توجهات بسیاری را به سوی خود جلب کنند.
شبکههای پیچشی گراف فضایی باید بتوانند یک تابع f را یاد بگیرند تا با جمعآوری ویژگیهای Xi خود و ویژگیهای Xi همسایه، نمایش گره vi را ایجاد کند. تابع جمعآوری باید تابعی باشد که نسبت به جایگشتهای ترتیبهای گره از جمله میانگین، مجموع و توابع ماکسیمم ثابت باشد. پس از جمعآوری ویژگیها یک تبدیل غیر خطی Non-linear transformation همچون Relu/Tanh بر روی خروجیها اعمال میشود. برای شناخت قابلیتهای یک گره کافی است چندین لایه پیچشی گراف را با یکدیگر پشته کنید. هر یک از لایههای پنهان GCN تکرار عملیات جمعآوری است که به دنبال آن فعالسازی غیرخطی Non-linear activation
میآید. هر تکرار / لایه از نمایشهای گره تکرار / لایه قبلی استفاده میکند تا نمایشهای گره کنونی را بگیرد.
اولین لایه GCN گردش اطلاعات میان همسایههای مرتبه یکم First-order neighbours را آسان میکند. دومین لایه اطلاعات را از همسایههای مرتبه یکم، به عبارت دیگر از همسایههای همسایه، میگیرد. این کار به همین ترتیب ادامه پیدا میکند و سپس با پشته کردن چندین لایه، نمایش نهایی و پنهان هر گره پیامی از همسایههای بعدی دریافت میکند.
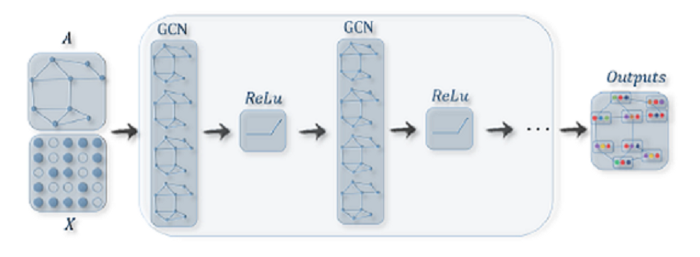
GCNها در سطح گره اجرا میشوند تا گرافها به ساختارهای فرعی سطح بالا تبدیل شوند، در مقابل ماژولهای ادغام گراف
Graph pooling modules میتوانند با لایه GCN جاگذاری شوند. از اینگونه طراحی معماری میتوان برای استخراج نمایشهایی در سطح گراف و همچنین انجام مسائل طبقهبندی گراف استفاده کرد.
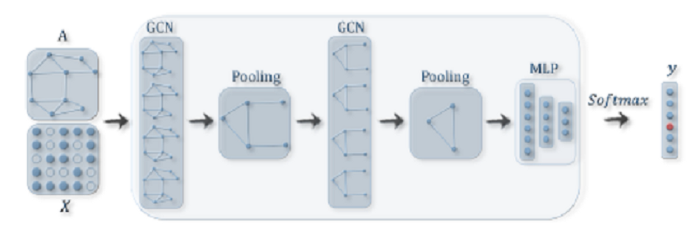
با توجه به اینکه کارایی GCNها به صورت مداوم ارتقا پیدا میکند، کیفیت عملکرد آنها در بسیاری از حوزها ارتقا پیدا میکند و از این روی معماری پایه بسیاری از مدلهای GCN را تشکیل میدهند.
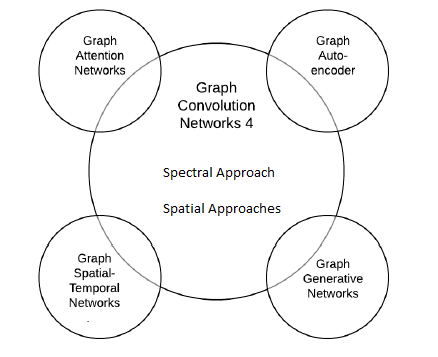
در ادامه فهرستی از معماریهای شبکههای عصبی گراف پیچیدهتر ارائه شده که برای حل مسائل مختلفی میتوان از آنها استفاده کرد:
- شبکههای توجه گرافی Graph Attention Networks
- خودرمزنگارهای گراف Graph Auto-Encoders
- شبکههای مولد گراف Graph Generative Networks
- شبکههای فضا-زمانی گراف Graph Spatio-Temporal Networks
شبکههای توجه گرافی
مکانیزم توجه Attention mechanisms در مسائل توالی محور sequence-based تقریباً به یک اصل اساسی تبدیل شده است. مکانیزمهای توجه قابلیت آن را دارند که بر روی مهمترین بخشهای ورودی متمرکز شوند. قابلیت مکانیزمهای توجه در تمرکز کردن بر روی مهمترین قسمتهای ورودی به ویژه در مسائلی همچون ترجمه ماشینی و درک زبان طبیعی سودمند است. افزایش ظرفیت مدلهای مکانیزم توجه موجب شده شبکههای عصبی گراف بتوانند از مزایای مدل توجه بهرهمند شوند. شبکههای توجه نموداری مشابه GCNها هستند و با استفاده از یک تابع جمعآوری نمایشهای گرههای همسایه، گامهای تصادفی Random walks یا خروجیهای مدلهای گوناگون را به یکدیگر متصل میکند تا یک نمایش جدید یاد بگیرد. تفاوت کلیدی میان شبکههای توجه نموداری و GCNها این است که شبکههای توجه نموداری از مکانیزمهای توجه استفاده میکنند که وزنهای بزرگتری به گرههای مهمتر، گامها یا مدلهای اعمال میکند. وزنهای توجه با استفاده از یک شبکه عصبی و در یک چارچوب نقطه به نقطه End-to-end framework یاد گرفته میشوند که شامل معماری عصبی گراف Graph neural architecture و شبکه عصبی توجه Attention neural network است.
برای اینکه بدانیم مکانیزم توجه چگونه به داده هایی با ساختاز گراف Graph-structured data اعمال میشود، ابتدا باید بررسی کنیم که اطلاعات گره همسایه چگونه با استفاده از مدلهای توجه برای به دست آوردن نمایش گره کنونی جمعآوری میشوند. در تصاویر مقابل این تفاوتها به تصویر کشیده شده است:

در تصویر (a) زمانیکه GCNها در طول فرایند جمعآوری وزن غیرپارامتری aij را به همسایه vj از vi اعمال میکنند، شبکه توجه نموداری، در تصویر (b)، با استفاده از معماری نقطه به نقطه شبکه عصبی وزن aij را ذخیره میکند و در نتیجه گرههای مهمتر، وزن بزرگتری دریافت میکنند.
به همین ترتیب برای گامهای تصادفی مبتنی بر GNN وزنهای تصادفی مختلف به گامهای مختلف اعمال میشود. مزیت شبکههای توجه نموداری این است که این شبکهها میتوانند به صورت انطباقی اهمیت هر همسایه را یاد بگیرند. با این وجود از آنجاییکه وزنهای توجه میان هر جفت همسایه باید محاسبه شود، هزینه محاسبه و همچنین میزان حافظهای که اشغال میشود به سرعت افزایش پیدا میکند.
خودرمزنگارهای گراف
هدف خودرمزنگارهای گراف این است که با استفاده از یک رمزنگار بُردارهایی با ابعاد کم را یاد بگیرد و سپس با استفاده از یک رمزگذار، گراف را بازسازی کند. این بُردارها میتوانند در سطح گره باشند، به عبارت دیگر یک بُردار به ازای هر گره یک نمایش ماتریس متراکم با ابعاد کم Dense low-dimensional matrix representation برای گراف ایجاد میکند. از سوی دیگر بُردارها میتوانند در سطح گراف باشند؛ منظور از بُردار در سطح گراف بُرداری است که تمامی اطلاعات گره و ساختاری گراف را ذخیره میکند. از آنجاییکه خودرمزنگارهای گراف یک نمایش برداری میانی Intermediate vector representation ایجاد میکنند، یکی از روشهای رایج و متداول برای یادگیری تعبیه گراف Graph embedding هستند.
یک روش دیگر برای تعبیه گره Node embedding این است که از پرسپترونهای چند لایه Multi-layer perceptrons به عنوان رمزنگار استفاده شود؛ در این حالت رمزگذار از طریق مکانیزمهای پیشبینی لینک، آمارههای گره مجاور از جمله لبههای میان گرهها را بازسازی میکند. رمزنگار میتواند اطلاعات مرتبه یکم و همچنین اطلاعات مرتبه دوم گره را ذخیره کند. در گرافهای ساده Plain graphs، بسیاری از الگوریتمها به صورت مستقیم ماتریس مجاورت را پردازش میکنند تا یک ماتریس متراکم با اطلاعات غنی ایجاد کنند. در گرافهای دارای ویژگی Attributed graphs، مدلهای خودرمزنگار گراف از GCNها به عنوان یکی از اجزای سازنده رمزگذار استفاده میکنند. نمونه دیگری از مدلهای خودرمزنگار گراف از مکانیزمهای مولد گراف Graph generative mechanisms ( که در قسمت بعدی توضیح داده خواهد شد) استفاده میکند تا گراف را از تعبیهها بازسازی کند.
تصویر مقابل نشاندهنده ساختار مدل خودرمزنگار گراف است:
رمزنگار برای به دست آوردن نمایشهای پنهان Latent representations هر یک از گرهها از لایههای GCN استفاده میکند. رمزگذار فاصله دوبهدو Pair-wise distance میان بُردارهای گره Node vector که رمزنگار ایجاد کرده محاسبه میکند. پس از اعمال یک تابع فعالسازی غیرخطی، رمزگذار ماتریس مجاورت گراف Graph adjacency matrix را بازسازی میکند. تمام مدل به گونهای آموزش دیده که یک فاصله دوبهدو ساده میان بُردارهای گره محاسبه شده برای بازسازی اطلاعات لبه گراف کافی است. به عبارت دیگر رمزنگار و رمزگذار به طور مشترک آموزش میبینند، در نتیجه نمایشهای یادگرفتهشده گره به گونهای هستند که رمزگذار میتواند مکمل رمزنگار باشد.
پس از آموزش ماژول رمزگذار را میتوان قطع کرد تا فقط بردارها را ایجاد کند و از آنها به عنوان گراف / تعبیه گره استفاده کند که میتوان از آنها به عنوان ورودی برای پرادازش بالا به پایین Downstream processing استفاده کرد.
شبکههای مولد گراف
شبکههای مولد گراف (GGN) سعی میکنند مطابق با توزیع داده و با در نظر گرفتن برخی محدودیتها، ساختارهایی از داده ایجاد کنند. به عبارت دیگر این شبکهها تلاش میکنند موجودیتها و روابط آنها، که در دادهها وجود دارند، را ثبت و ذخیره کنند و تلاش میکند آنها را به عنوان ساختارهای گرافیکی الگو قرار دهد. در مقابل GGNها ممکن است تلاش کنند با در نظر گرفتن مجموعهای از گرافهای گرافی با ویژگیهای خاص ایجاد کنند. یکی از مهمترین موارد کاربرد GGNها سنتز ترکیبات شیمیایی Chemical compound synthesis است. در یک گراف شیمیایی، اتمها به عنوان گره و پیوندهای شیمیایی به عنوان لبه در نظر گرفته میشوند. در این حالت هدف این است که با در نظر گرفتن مجموعهای از مولکولهای موجود، مولکولهای قابل سنتز که دارای ویژگیهای فیزیکی و شیمیایی خاصی هستند شناسایی شوند. یکی دیگر از موارد کاربرد GGNها استفاده از این شبکهها در پردازش زبان طبیعی است؛ در حوزه پردازش زبان طبیعی معمولاً یک گراف دانش یا گراف معنایی در یک جمله مشخص قرار میگیرد.
با وجود این، ایجاد یک گراف با در نظر گرفتن توزیع تجربی گراف Graph empirical distribution فرایند دشواری است و دلیل عمده آن هم این است که گرافها ساختارهای دادهای پیچیدهای هستند. روش دیگر این است که فرایند تولید را در قالب گرهها و لبهها در آوریم. مدلهای مولد عمیق گراف (DGMG) Deep Generative Models of Graph (DGMG) (نمونهای از این روش است. DGMG از GCN برای به دست آوردن نمایشهای بردار گرافهای ورودی موجود استفاده میکند. فرایند تصمیمگیری راجع به ایجاد گرهها و لبهها در این بردار انجام میشود. DGMGبه طور مکرر یک گره به گراف در حال رشد ارائه میدهد تا زمانیکه به یک معیار توقف دست پیدا کند. در هر مرحله، پس از افزودن یک گره جدید، DGMG به طور مکرر راجع به اضافه کردن یک لبه به گره اضافه شده، تا زمانی که تصمیم نادرست شود، تصمیمگیری میکند.
رویکرد دیگر مبتنی بر شبکههای مولد تخاصمی (GANs) Generative Adversarial Networks (GANs) (است که در تولید تصاویر مورد استفاده قرار میگیرند. اما در شبکههای تخاصمی به جای استفاده از شبکههای عصبی پیچشی از شبکههای پیچشی گراف به عنوان اجزای سازنده استفاده میشود. GAN از یک مولد و یک متمایزکننده تشکیل شده که با یکدیگر رقابت میکنند تا نرخ دقت مولد افزایش پیدا کند. ابتدا مولد از یک توزیع داده یک گراف کاندید ایجاد میکند. معمولاً این گراف انتخابی گراف جعلی نامیده میشود. سپس متمایزکننده باید نمونههای جعلی را از دادههای تجربی تشخیص دهد. علاوه بر متمایزکننده میتوان از شبکه پاداش Reward network استفاده کرد تا گرافهای ایجاد شده را ترغیب کرد ویژگیهای خاصی کسب کنند. متمایزکننده و شبکه پاداش به نمایش برداری گراف جعلی تغذیه میشوند؛ متمایزکننده و همچنین شبکه پاداش یک امتیاز خروجی میدهند که به عنوان بازخورد مولد استفاده میشود.
تصویر مقابل نشاندهنده معماری است:
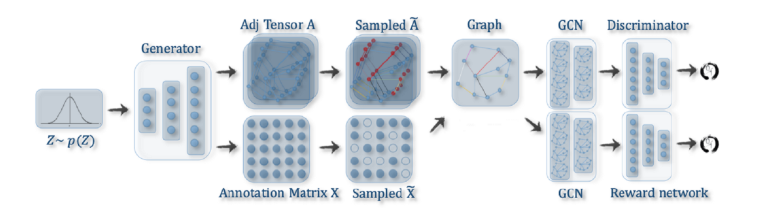
یکی از نقاط ضعف دو رویکردی که به آنها اشاره شد این است که به دلیل اینکه فضای خروجی گراف با n گره n^2 است، نمیتوانند گرافهای بزرگها را مقیاسبندی کنند.
شبکههای فضا-زمانی گراف
گرافهای فضا- زمانی ساختارهای گرافی هستند که در آنها ویژگیهای گره و یا لبه با زمان t تغییر میکند. برای مثال، شبکههای ترافیک جادهای را میتوان به عنوان گراف در نظر گرفت که در آنها هر موقعیت کلیدی یک گره است و حسگر موجود در آن موقعیت سرعت ترافیک را در آن موقعیت در چند نوبت کنترل میکند؛ در این حالت، مقادیر گره ( سرعت ترافیک در آن موقعیت) با زمان تغییر میکند. لبهها را هم میتوان فاصله میان دو حسگر یا گرهها موقعیت در نظر گرفت. با استفاده از این اطلاعات زمانی که از گرافهای زمانی شبکههای ترافیک جادهای به دست آمده، ترافیک را برای گام زمانی آتی گرههای گراف فضا-زمانی میتوان پیشبینی کرد.
یکی از مشکلاتی که در پیشبینی ترافیک با آن مواجه میشویم، مشکل پیشبینی میزان تقاضا برای تاکسی است که به طور گسترده در سیستمهای حمل و نقل هوشمند مورد استفاده قرار میگیرد. در پیشبینی میزان تقاضا برای تاکسی، تاکسیها از پیش تقسیم میشوند تا جابهجای مسافران با مشکل مواجه نشود و تعداد تاکسیهای خالی که باعث هدر رفتن انرژی و افزایش تراکم ترافیک میشود در سطح خیابان کاهش یابد. با توجه به افزایش بازارهای حملونقل اینترنتی از جمله Uber و Ola پیشبینی میزان تقاضا برای تاکسی مفید خواهد بود. در این مورد نیز مثال پیشبینی ترافیک، موقعیتهای کلیدی را میتوان گرههایی با ویژگیهایی از جمله ترافیک، شرایط آبوهوایی در آن موقعیتها در نظر گرفت؛ همزمان با تغییر روز و ماه این ویژگیها نیز تغییر میکنند. برچسبهای گره میتوانند تعداد تاکسیهای مورد نیاز در یک منطقه خاص باشند. در این مورد نیز تعداد تاکسیهای مورد نیاز مطابق با زمان تغییر میکند و مشکلی که با آن مواجه هستیم پیشبینی این مقادیر برای گام زمانی آتی است.
ایده اصلی شبکههای فضا-زمانی این است که به طور همزمان وابستگی فضایی و وابستگی زمانی در نظر گرفته شوند. بسیاری از رویکردهای امروزی برای ذخیره وابستگی فضایی از GCNها و همچنین RNN و CNN استفاده میکنند تا وابستگی زمانی را مدلسازی کنند. یکی از این رویکردها شبکه عصبی بازگشتی پیچشی انتشار (DCRNN) Diffusion Convolution Recurrent Neural Network (DCRNN) نامیده میشود؛ در این رویکرد پیچش انتشار به عنوان پیچش گراف برای ذخیره وابستگی فضایی ارائه میشود و از معماری دنباله به دنباله Sequence-to-sequence architecture به همراه واحد بازگشتی (GRU) Gated recurrent unit (GRU) درگاهی ( برای ذخیره وابستگی زمانی استفاده میکنند. DCRNN ورودی GRU را با استفاده از یک لایه پیچشی گراف (انتشار) پردازش میکند، در نتیجه واحد بازگشتی به طور همزمان اطلاعات را از گام زمانی قبلی و اطلاعات همسایه را از پیچش گراف دریافت میکند. مزیت DCRNN این است که به دلیل معماریهای شبکه بازگشتی میتواند وابستگیهای بلند مدت را کنترل و اداره کند.








