آیا BorutaShap بهترین الگوریتم انتخاب ویژگی است؟

انتخاب ویژگی یکی از مراحل مهم در خط‌پایه یادگیری ماشین است که اغلب مورد غفلت قرار می‌گیرد. فرآیند انتخاب ویژگی شامل کاهش ابعاد فضای ورودی Input space از طریق انتخاب زیرمجموعه‌ای مرتبط از ویژگی‌های آن (ورودی) می‌شود. شاید از خود بپرسید چرا این فرآیند حائز اهمیت است؟ زیرا:

1. کاهش اندازه و پیچیدگی مدل، تفسیرپذیری آن را تسهیل می‌کند؛

2. هرچه مدل کوچک‌تر باشد، آموزش آن سریع‌تر و آسان‌تر است. همچنین زمانی که ویژگی‌های کمتری وجود داشته باشند، خط‌پایه مهندسی ویژگی Feature engineering pipeline و جمع‌آوری داده ساده‌سازی خواهند شد.

3. انتخاب ویژگی می‌تواند با حذف ویژگی‌های نویزدار Noisy features مشکل بیش‌تطبیقی overfitting را نیز رفع کند و بدین ترتیب به مدل‌ها قابلیت تعمیم به داده‌‎های جدید بخشیده و دقت آن‌ها را افزایش دهد.

ایده زیربنایی استفاده از یک الگوریتم انتخاب ویژگی این است که دیتاست‌های جدید مقادیری ویژگی زائد redundant و غیرمرتبط دارند که می‌توان آن‌ها را بدون از دست دادن اطلاعات حذف کرد.

الگوریتم انتخاب ویژگی را می‌توان به دو مؤلفه تجزیه کرد: یک تکنیک جستجو که زیرمجموعه‌های جدید را معرفی می‌کند، و یک معیار ارزیابی Evaluation metric که برای امتیازدهی به این زیرمجموعه‌ها استفاده می‌شود. بنابراین می‌توان گفت ساده‌ترین الگوریتم انتخاب ویژگی الگوریتمی است که هر کدام از زیرمجموعه‌های ممکن از ویژگی‌های ورودی را آزمایش کرده و تصمیم می‌گیرد کدام یک از آن‌ها نرخ خطای مدل را به حداقل می‌رسانند.

با این حال این جستجو بسیار گسترده است و برای هیچ دیتاست بزرگی از نظر محاسباتی قابل انجام نخواهد بود، زیرا در چنین دیتاست‌هایی تعداد زیرمجموعه‌های ممکن بسیار زیاد هستند. تعداد زیرمجموعه‌ها را می‌توان از این فرمول حساب کرد:

در این فرمول n تعداد ویژگی‌های یک دیتاست را نشان می‌دهد.

چه رویکردهایی برای انتخاب ویژگی وجود دارند؟

رویکردهای انتخاب ویژگی را می‌توان بر اساس نحوه ترکیب الگوریتم انتخاب با ساختار مدل، به سه طبقه تقسیم کرد: فیلتر، wrapper و تعبیه‌شده embedded.

روش‌های فیلتر

این روش‌ها زیرمجموعه‌های ویژگی‌ها را مستقل از مدل انتخاب می‌کنند. ایده اصلی این روش‌ها استفاده از نوعی معیار همبستگی Correlation metric با متغیر به منظور پیش‌بینی است. برخی از معیارهای رایج همبستگی عبارت‌اند از: اطلاعات متقابل Mutual information، اطلاعات متقابل نقطه‌ای Point-wise mutual information، و یا حتی معیار ساده‌تر، مانند ضریب همبستگی پیرسون Pearson coefficient. از آن‌جایی که مبنای روش‌های فیلتر این معیارهای آماری هستند، معمولاً نسبت به روش‌های wrapper نیاز به محاسبات سبک‌تری دارند.

با این حال زیرمجموعه‌ای که از ویژگی‌ها انتخاب می‌شود، متناسب با مدل تنظیم نمی‌گردد و روابط و تعاملات بین خود متغیرها نیز در نظر گرفته نمی‌شود.

روش‌های wrapper

روش‌های wrapper از یک مدل پیش‌بینی برای امتیازدهی به زیرمجموعه‌های ویژگی‌ها استفاده می‌کنند؛ بدین صورت که هر زیرمجموعه جدید برای آموزش مدلی کاربرد دارد که بعداً روی یک زیرمجموعه دیگر آزمایش می‌شود. خطای پیش‌بینی محاسبه و به عنوان مقدار بازنمایی Representative score آن زیرمجموعه خاص استفاده می‌شود.

همانطور که می‌دانید آموزش یک مدل جدید بر روی هر یک از زیرمجموعه‌ها از نظر محاسباتی پرهزینه است. با این وجود این روش‌ها معمولاً بهترین مجموعه ویژگی را برای یک مدل یا مسئله خاص ارائه می‌دهند. یک نمونه از روش‌های wrapper، روش رگرسیون گام به گام Stepwise regression است.

روش‌های تعبیه‌شده

این دسته از روش‌ها سعی دارند با اجرای فرآیند انتخاب ویژگی به عنوان بخشی از ساختار خود مدل، نقاط قوت دو روش قبلی را ترکیب کنند. نمونه واضح این دسته از روش‌ها، روش رگرسیون LASSO است که ضرایب رگرسیون را با L1 penalty جریمه می‌نماید. هر ویژگی‌ که ضریب رگرسیون غیرصفر داشته باشد توسط الگوریتم LASSO انتخاب خواهد شد.

Boruta چیست؟

Boruta یکی از روش‌های برجسته در بین روش‌های تعبیه‌شده می‌باشد که حول مدل‌های جنگل تصادفیRandom forest (RF) ساخته شده است. این الگوریتم از بسط و گسترش مقاله Party on طراحی شده و اهمیت ویژگی را از طریق مقایسه ارتباط ویژگی‌های واقعی با ویژگی‌های کاوشگر‌های تصادفیRandom probes تعیین می‌کند. به طور خلاصه می‌توان گفت این الگوریتم بدین شکل عمل می‌کند:

1. در شروع کار، از همه ویژگی‌های موجود در دیتاست کپی‌هایی با نام shadow + feature_name (سایه + نام ویژگی) ایجاد می‌کند. سپس این ویژگی‌های جدید را به هم می‌ریزد تا همبستگی‌های بین آن‌ها و متغیرهای پاسخResponse variables را از بین ببرد.

2. یک رده‌‎بند random forest را روی داده‌های بسط یافته با ویژگی‌های کپی‌شده shadow اجرا می‌کند. سپس با استفاده از یک معیار اهمیت ویژگی، ویژگی‌ها را رتبه‌بندی می‌کند (الگوریتم اصلی معیار اهمیت جایگشت permutation را به کار می‌برد).

3. با استفاده از حداکثر امتیاز اهمیتِ ویژگی‌های سایه، یک آستانه threshold ایجاد می‌کند. سپس برای هر ویژگی که از این آستانه عبور کند یک نرخ اصابتhit اختصاص می‌دهد.

4. برای هر ویژگی که به معیار نپیوسته است، یک آزمون برابری T اجرا می‌کند.

5. ویژگی‌هایی که امتیاز اهمیت آن‌ها خیلی از آستانه پایین‌تر است، غیرمهم شناخته شده و از فرآیند حذف می‌شوند. ویژگی‌هایی که امتیاز اهمیت آن‌ها به طرز معناداری از آستانه بالاتر است مهم شناخته می‌شوند.

6. همه ویژگی‌های سایه حذف شده و این فرآیند آنقدر تکرار می‌گردد تا یک معیار اهمیت به هر ویژگی اختصاص داده شود یا تا زمانی که الگوریتم به حدی از اجراهای جنگل تصادفی که از قبل تنظیم‌شده برسد.

به نظر من Boruta یکی از بهترین الگوریتم‌های انتخاب ویژگی است که در دست داریم، زیرا نتایجی دقیق و باثبات ارائه می‌دهد. با این حال این الگوریتم می‌تواند از چند لحاظ (به خصوص از نظر پیچیدگی محاسباتی و معیاری که برای رتبه‌بندی اهمیت ویژگی به کار می‌برد) ارتقاء یابد. در همین راستا در این قسمت به معرفی SHAP می‌پردازیم.

SHAP (SHapely Additive exPlanations)

SHAP رویکردی یکپارچه است که خروجی هر مدل یادگیری ماشینی را توضیح می‌دهد. روش SHAP بین نظریه بازی Game theory با توضیحات محلی Local explanations رابطه برقرار کرده تا یک تشریح‌گرexplainer پایا و دقیق ایجاد کند.

SHAP سهم حاشیه‌ای میانگین Average marginal contribution را برای هر ویژگی در همه جایگشت‌ها در یک سطح محلی محاسبه می‌کند. از آن‌جایی که Shap یک روش جمعی است، میانگین مقدار هرکدام از این سهم‌های حاشیه‌ای می‌توانند برای دستیابی به یک میزان اهمیت ویژگی کلی Global feature importance استفاده شوند.

روش SHAP حوزه تعامل‌پذیری interoperability مدل‌ها را به یکپارچگی رسانده است و از نظر من یکی از تأثیرگذارترین دستاوردهای اخیر جامعه یادگیری ماشینی به حساب می‌رود. پیشنهاد می‌کنم زمینه تعامل‌پذیری یادگیری ماشینی را با دقت بیشتری مورد مطالعه قرار دهید، بدین منظور بهتر است از مقاله «راهی برای توضیح‌پذیر کردن مدل‌های جعبه سیاه» کریستوفر مولنار Christopher Molnar شروع کنید.

با تمام این‌ها می‌توان گفت یک نقطه‌ضعف این رویکرد این است که تشریح‌گر هسته Kernel explainer آن باید سهم حاشیه‌ای هر ائتلاف coalition موجود در دیتاست را ایجاد و سپس اندازه‌گیری کند؛ این اعمال از نظر محاسباتی سنگین و پرهزینه هستند. خوشبختانه از آن‌جایی که الگوریتم Boruta برمبنای جنگل تصادفی طراحی شده، یک راهکار TreeSHAP وجود دارد که رویکردی کارآمد و به صرفه را برای برآورد در مدل‌های درخت-محور ارائه می‌دهد و بدین ترتیب پیچیدگی زمانی را کاهش می‌دهد.

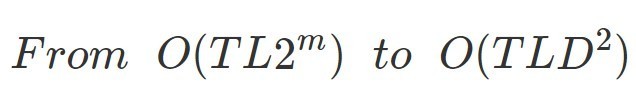
در این فرمول، T تعداد درخت‌‌ها، L ماکزیمم تعداد برگ‌‌های هر درخت و D ماکزیمم عمق هر درخت را نشان می‌‌دهد.

مشکل Boruta/Boruta+Shap

پیش‌‌تر دو مشکل اساسی الگوریتم Boruta را مطرح کردیم (اولی پیچیدگی محاسباتی و دومی دقت و پایایی  رده‌‌بندی ویژگی‌‌ها بود). هردوی این مشکلات به آسانی و با تغییر الگوریتم اهمیت ویژگی (اهمیت جایشگت) با تشریح‌‌گر TreeSHAP قابل حل هستند.

الگوریتم Boruta برای تکرار دوباره، از طریق ایجاد این جایگشت‌‌های تصادفی از ویژگی‌‌های اصلی به دیتاست نویز وارد می‌‌کند. سپس یک مدل جنگل تصادفی را با این داده‌‌های نویزدار تطابق داده و از رتبه-بندی اهمیت ویژگی استفاده می‌‌کند تا در مورد نگه‌‌ داشتن یا نداشتن یک ویژگی تصمیم بگیرد.

در روش‌‌های گروهی درختی Tree ensemble methods مقادیر اهمیت کلی ویژگی به سه روش اصلی محاسبه می‌‌شوند:

1. Gain : این مورد روشی قدیمی است و با جمع کاهش تابع زیان یا ناخالصی یک ویژگی که از همه‌‌ی قسمت‌‌ها (شاخه‌‌های درخت) به دست می‌‌آید محاسبه می‌‌شود. روش بهره به صورت پیش‌فرض در رو‌‌ش‌‌های گروهی درختی Sickit-learn برای تعیین اهمیت ویژگی‌‌ها استفاده می‌‌گردد.
2. شمار شاخه‌‌ها Split count : در این روش به سادگی تعداد دفعات استفاده از یک ویژگی برای ایجاد شاخه‌‌ (قطعات) در ساختار درخت را می‌‌شمارند.
3. جابجایی permutation : در این روش مقادیر یک ویژگی به صورت تصادفی در مجموعه‌‌ی آزمایشی جابجا می‌‌شود؛ سپس تغییراتی که در خطای مدل رخ می‌‌دهد مشاهده می‌‌گردد. اگر مقدار یک ویژگی حائز اهمیت باشد، جابجا کردن آن باید تغییر بزرگی در خطای مدل ایجاد کند.

کاربرد اصلی بسته‌‌ Boruta در زبان برنامه‌‌نویسی R رویکرد جابجایی را به کار می‌‌برد. با این‌‌که جابجایی پایاترین رویکرد در میان سه روش مذکور است، مقیاس‌‌پذیری ضعیفی دارد.

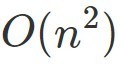
در این فرمول n تعداد ویژگی‌‌‌‌هاست.

نکته‌‌‌‌ی تعجب‌‌‌‌برانگیز این است که بسته‌‌‌‌ی Boruta در زبان پایتون پیاده‌‌‌‌سازی نمی‌‌‌‌شود. البته در Boruta-py قابل اجرا می‌‌‌‌باشد که در آن از میانگین کاهش ناخالصی Impurity به عنوان مقدار اهمیت ویژگی استفاده می‌‌‌‌کند (روش‌‌‌‌های جابجایی و حتی شمار شاخه‌‌‌‌ها با وجود سرعت و کاربرد گسترده‌‌‌‌ای که دارند‌‌‌‌، روش‌‌‌‌های قابل اتکایی برای اندازه‌‌‌‌گیری اهمیت کلی ویژگی به شمار نمی‌‌‌‌روند).

مقایسه

برای ارزیابی مزایای روش BorutaShap از پیاده‌‌‌‌سازی آن در Python استفاده کردم که شامل هر سه معیار اندازه‌‌‌‌گیری (بهره، Shap و جابجایی) می‌‌‌‌شود. سپس روش‌‌‌‌های متفاوتی را روی سه دیتاست آزمایشی اجرا و مقایسه کردم تا عملکرد نسبی آن‌‌‌‌ها را بسنجم.

یک Random Forest  از Sickit-learn به عنوان مدل پایه‌‌‌‌ای مقایسه‌‌‌‌ها مورد استفاده قرار گرفت. با این حال باید به این نکته توجه کرد که معیارهای اهمیت Shap و جابجایی، هر دو model-agnostic هستند؛ در صورتی که معیار بهره فقط در مدل‌‌‌‌های درخت‌‌‌‌محور کاربرد دارد.

معیار اهمیت Gain : به منظور محاسبه‌‌‌‌ی معیار بهره، روش پایه‌‌‌‌ای feature_importances_ در sickit-learn به کار برده می‌‌‌‌شود. این رویکرد به نام‌‌‌‌های اهمیت  gini و ناخالصی کاهشی میانگین Mean decrease impurity نیز شناخته می‌‌‌‌شود. معیار اهمیت بهره را می‌‌‌‌توان بدین صورت تعریف کرد: کاهش کلی در ناخالصی گره که براساس احتمال دستیابی آن گره به بالای همه‌ی درخت‌های گروه، به آن وزن تعلق می‌گیرد.

معیار اهمیت جابجایی : برای این معیار از اجرای permutation_importance استفاده شد. این روش با درهم‌‌‌‌ریختگی تصادفی یک ویژگی در دیتاست، میانگین کاهش را در صحت مدل محاسبه می‌‌‌‌کند. این فرآیند درهم‌‌‌‌ریختگی ویژگی باعث می‌‌‌‌شود ارتباط ویژگی با هدف قطع شود؛ بدین ترتیب اگر دقت مدل کاهش یابد حاکی از این خواهد بود که مدل چقدر به آن ویژگی وابسته است.

معیار اهمیت SHAP : همانطور که پیش‌‌‌‌تر بیان شد، بسته‌‌‌‌ی پایتونی SHAP (که توسط اسلاندبرگSlundburg ساخته شده) برای محاسبه‌‌‌‌ی مقادیر اهمیت به کار برده می‌‌‌‌شود. در این بسته چندین تشریح‌‌‌‌گر گوناگون وجود دارند که برای ساختار مدل‌‌‌‌های متفاوت بهینه‌‌‌‌سازی شده‌‌‌‌اند. بنابراین از TreeExplainer برای توضیح رفتار مدل random forest استفاده میکنیم که روشی سریع و منحصر به مدل‌‌‌‌های درخت-محور است (و جایگزین خوبی برای KernelSHAP به حساب می‌‌‌‌رود).

دیتاست Ozone

دیتاست‌‌‌‌ آلودگی Los Angeles ozone pollution شامل 366 مشاهده‌‌‌‌ی روزانه از 13 متغیر از سال 1976 می‌‌‌‌شود. مسئله‌‌‌‌ این دیتاست رگرسیون است؛

هدف دیتاست پیش‌‌‌‌بینی ماکزیمم روزانه‌‌‌‌ی مقدار میانگین مطالعه‌‌‌‌ی اوزون در یک ساعت Daily maximum one-hour-average ozone reading Slundburg (v4) با استفاده از چندین متغیر است. اسامی واقعی این متغیرها عبارت‌اند از:

• V1 – ماه: 1= ژانویه، … 12= دسامبر
• V2 – روز ماه
• V3 – روز هفته: 1= دوشنبه، … 7= یکشنبه
• V4 – ماکزیمم روزانه‌‌‌‌ی میانگین مطالعه‌‌‌‌ی اوزون در یک ساعت
• V5 – 500 میلی‌‌‌‌بار فشار ارتفاع (m) که در پایگاه نیروی هوایی وندنبرگ Vandenberg AFB اندازه‌‌‌‌گیری می‌شود.
• V6 – سرعت باد (بر حسب مایل بر ساعت) در فرودگاه بین‌‌‌‌المللی لس‌‌‌‌آنجلس (LAX)
• V7 – رطوبت (به صورت درصدی) در فرودگاه بین‌‌‌‌المللی لس‌‌‌‌آنجلس
• V8 – دمای هما (بر حسب فارنهایت) که در سندبرگSandburg, CA کالیفرنیا اندازه‌‌‌‌گیری می‌‌‌‌شود.
• V9 – دمای هوا (بر حسب فارنهایت) که در ال‌‌‌‌مونتهEl Monte, CA کالیفرنیا اندازه‌‌‌‌گیری می‌‌‌‌شود.
• V10 – جابجایی ارتفاع پایه Inversion base height در فرودگاه بین‌‌‌‌المللی لس‌‌‌‌آنجلس
• V11 – گرادیان فشار (بر حسب میلی‌‌‌‌متر جیوه) از فرودگاه بین‌‌‌‌المللی لس‌‌‌‌آنجلس تا دگتDaggett, CA کالیفرنیا
• V12 – وارونگی دما Inversion base temperature (بر حسب فارنهایت) در فرودگاه بین‌‌‌‌المللی لس‌‌‌‌آنجلس
• V13 – دید پرواز (بر حسب مایل) در فرودگاه بین‌‌‌‌المللی لس‌‌‌‌آنجلس

همانطور که در نمودارهای پایین مشاهده می‌‌‌‌کنید، هر سه الگوریتم Boruta به عنوان متغیر در زیرمجموعه‌‌‌‌های دیتاست اوزون به کار رفته‌‌‌‌اند و هر متغیر نتایج متفاوتی ارائه داده است. معیارهای Shap و بهره زیرمجموعه‌‌‌‌های مشابهی ایجاد کردند، اما Shap متغیر V1 یا ماه را به عنوان یک ویژگی معنادار تفسیر کرده است. معیار جابجایی بسیار آسان‌‌‌‌گیرتر  بوده و موارد V1 و V5 را ویژگی‌‌‌‌های معناداری تشخیص داد.

در شکل بالا نتیجه‌‌‌‌‌ی استفاده از روش Boruta برای هرویژگی به صورت نمودار جعبه‌‌‌‌‌ای نمایش داده شده است. مقادیر سبز ویژگی‌‌‌‌‌های پذیرفته‌‌‌‌‌شده، مقادیر قرمز ردشده و آبی هم ویژگی‌‌‌‌‌های سایه را نشان می‌‌‌‌‌دهند. محور y با استفاده از یک تبدیل لگاریتمیLog transform مقیاس‌‌‌‌‌بندی شده است. هرکدام از متغیرها معیاری متفاوت از مقادیری که به منظور مقایسه نرمال‌‌‌‌‌سازی شده‌‌‌‌‌ بودند تحویل می‌‌‌‌‌دهند.

دیتاست سرطان سینه

دیتاست Wisconsin breast cancer 569 نمونه با 32 ویژگی را در برمی‌‌‌‌‌گیرد. هر مورد مشاهده مربوط به یک بیمار است و مسئله تشخیص خوش‌‌‌‌‌خیم یا بدخیم بودن اسکن‌‌‌‌‌ها می‌‌‌‌‌باشد.

ویژگی‌‌‌‌‌های این دیتاست از تصاویر دیجیتالی FNA (آسپیراسیون سوزنی ظریف Fine needle aspiration ) که از توده‌‌‌‌‌های سرطانی سینه گرفته شده، محاسبه می‌‌‌‌‌شوند و مشخصات مربوط به هسته‌‌‌‌‌های سلول‌‌‌‌‌ها را توصیف می‌‌‌‌‌کنند. اطلاعاتِ ویژگی‌‌‌‌‌ها از این قرارند:

• a) شعاع (میانگین فاصله‌‌‌‌‌ نقاط روی محیط از مرکز)
• b) بافت (انحراف معیار مقادیر سیاه سفید )
• c) محیط
• d) مساحت
• e) همواری (تنوع محلی در طول شعاع‌‌‌‌‌ها)
• f) تراکم (محیط به توان دو تقسیم بر مساحت – 1.0)
• g) قوس (شدت قسمت‌‌‌‌‌های مقعر منحنی )
• h) نقاط مقعر (تعداد قسمت‌‌‌‌‌های مقعر منحنی)
• i) قرینگی
• j) بُعد فراکتال (تخمین خط مرزی -1)

میانگین، خطای استاندارد و بدترین یا بزرگ‌‌‌‌‌ترین (میانگین سه مقدار بزرگ‌‌‌‌‌تر) این ویژگی‌‌‌‌‌ها برای هر تصویر محاسبه شده و در نتیجه 30 ویژگی به دست می‌‌‌‌‌آید.

با استنباط از شکل پایین می‌‌‌‌‌توانیم نه تنها بین زیرمجموعه‌‌‌‌‌های تولید شده از ویژگی‌‌‌‌‌ها، بلکه بین رتبه‌‌‌‌‌بندی هرکدام از ویژگی‌‌‌‌‌ها هم تفاوت‌‌‌‌‌هایی مشاهده کنیم. این واقعیت که فقط SHAP تفسیر پایایی ارائه می‌‌‌‌‌دهد بدین معنی است که می‌‌‌‌‌توان برای نتیجه‌‌‌‌‌گیری در مورد رفتار کلی مدل‌‌‌‌‌ها از این خروجی‌‌‌‌‌ها استفاده کرد.

من به منظور ارزیابی کیفیت زیرمجموعه‌‌‌‌‌هایی که هر کدام از این سه روش تولید کرده‌‌‌‌‌اند، از اعتبارسنجی متقابل 5 برابری5 Fold cross validation برای هرکدام از سه زیرمجموعه‌‌‌‌‌ی حاصل انجام دادم و یافته‌‌‌‌‌های خود را در این جدول به نمایش گذاشته‌‌‌‌‌ام.

از این جدول متوجه می‌‌‌‌‌‌شویم که زیرمجموعه‌‌‌‌‌‌ی تولید شده توسط SHAP دقت کلسیفایر جنگل تصادفی را به مقدار یک درصد افزایش داده است. شاید این عدد چندان تأثیرگذار به نظر نرسد، اما قادر به کاهش زیرفضا subspace از 32 به 21 ویژگی بوده که خود یک کاهش 28 درصدی را نشان می‌‌‌‌‌‌دهد.

بدین ترتیب می‌توانیم مدلی دقیق‌‌‌‌‌‌تر و ساده‌‌‌‌‌‌تر داشته باشیم. نکته‌‌‌‌‌‌ای که باید مدنظر داشته باشیم این است که دقت روش بهره برابر با دقت روش Shap می‌‌‌‌‌‌باشد، ولی زیرمجموعه‌‌‌‌‌‌ای بزرگ‌‌‌‌‌‌تر و متفاوت از ویژگی‌‌‌‌‌‌ها انتخاب می‌‌‌‌‌‌کند. ستون آخر این جدول هم زمانی که هر روش نیاز داشته را نشان می‌‌‌‌‌‌دهد.

از این ستون می‌‌‌‌‌‌توانیم نتیجه بگیریم که روش بهره به طرز معناداری از دو روش دیگر سریع‌‌‌‌‌‌تر است؛ زیرا به خاطر استفاده از خود ساختار مدل، به تعداد مشاهدات وابسته نیست.

در این تصویر نیز مقادیر سبز آن ویژگی‌‌‌‌‌‌‌هایی هستند که پذیرفته‌‌‌‌‌‌‌ شده‌‌‌‌‌‌‌اند، مقادیر قرمز رده شده و آبی هم نشان‌‌‌‌‌‌‌دهنده‌‌‌‌‌‌‌ی اندازه‌‌‌‌‌‌‌ی ویژگی‌‌‌‌‌‌‌های سایه است. محور y با استفاده از تبدیل لگاریتمی مقیاس‌‌‌‌‌‌‌پذیر شده و از آن‌جایی که هرکدام از روش‌‌‌‌‌‌‌ها از معیارهای متفاوتی استفاده می‌‌‌‌‌‌‌کنند، مقادیر به دست‌‌‌‌‌‌‌آمده نرمال‌‌‌‌‌‌‌سازی شده‌‌‌‌‌‌‌اند.

دیتاست Madelon

براساس منبع کدی که بخش یادگیری ماشینی دانشگاه کالیفرنیا ارائه داده است، Madelon یک دیتاست مصنوعی است که نقاط‌‌‌‌‌‌‌داده‌‌‌‌‌‌‌ای را در برمی‌‌‌‌‌‌‌گیرد که در 32 خوشه گروه‌‌‌‌‌‌‌بندی شده‌‌‌‌‌‌‌، در رئوس هایپرمکعب 5 بُعدی Vertices of a five dimensional hypercube قرار گرفته‌‌‌‌‌‌‌ و به صورت تصادفی برچسب‌‌‌‌‌‌‌های +1  و -1 خورده‌‌‌‌‌‌‌اند.

این پنج بعد 5 ویژگی آگاهی‌دهنده Informative features را تشکیل می‌‌‌‌‌‌‌دهند. 15 ترکیب خطی از این ویژگی‌‌‌‌‌‌‌ها به یک مجموعه‌‌‌‌‌‌‌ از ویژگی‌‌‌‌‌‌‌های (زائد) آگاهی‌‌‌‌‌‌‌دهنده Redundant informative features اضافه شدند. سپس 480 ویژگی زائد تصادفی نیز اضافه شده‌‌‌‌‌‌‌اند و درنهایت دیتاستی شامل 4400 مشاهده و 500 ستون ایجاد گردید.

زیرمجموعه‌‌‌‌‌‌‌های تولیدشده از طریق این سه روش تفاوت معناداری با هم دارند؛ روش Shap پانزده ویژگی و روش‌‌‌‌‌‌‌های بهره و جایگشت تقریباً 19 و 20 ویژگی انتخاب می‌‌‌‌‌‌‌کنند. نکته‌‌‌‌‌‌‌ی جالب اینجاست که هر سه متغیر به دقت مشابهی دست یافتند، اما مدلی که از زیرمجموعه‌‌‌‌‌‌‌ی Shap تولید شد (با حدود 25% ویژگی کمتر از دور روش دیگر) همان دقت را به دست آورد.

همچنین از نظر میزان استقلال خطی از تعداد مشاهدات دیتاست هم باید بین روش جابجایی و Shap مقایسه‌‌‌‌‌‌‌ای انجام می‌‌‌‌‌‌‌گرفت. نتیجه‌‌‌‌‌‌‌ی این مقایسه نشان می‌‌‌‌‌‌‌دهد هر دو الگوریتم به زمان بسیار طولانی‌‌‌‌‌‌‌تری نسبت به روش بهره نیاز داشتند. نکته‌‌‌‌‌‌‌ی دیگر میزان تفاوت رتبه‌‌‌‌‌‌‌بندی ویژگی‌‌‌‌‌‌‌ها Feature ranking در این سه روش است؛ هر روش تفسیر خاص خود را از جنگل تصادفی ارائه می‌‌‌‌‌‌‌دهد.

دیتاست آنقدر بزرگ بود که تنها می‌‌‌‌‌‌‌‌توان متغیرهای پذیرفته شده را در یک تصویر به صورت واضح نشان داد.

پیچیدگی زمانی

هنگام انجام تجزیه‌‌‌‌‌‌‌‌تحلیل‌‌‌‌‌‌‌‌های بالا نکته‌‌‌‌‌‌‌‌ای که بسیار به چشم می‌‌‌‌‌‌‌‌خورد تفاوت‌‌‌‌‌‌‌‌های بین تعداد دفعات اجرای  هر روش بود. بنابراین تصمیم گرفتم دو طرح آزمایشی انجام دهم که استقلال هر روش را از تعداد ردیف‌ها  و مشاهدات نشان دهد. همانطور که پایین‌‌‌‌‌‌‌‌تر به نمایش گذاشته شده، روش بهره/gini به اندازه‌‌‌‌‌‌‌‌ی دیتاست وابسته نیست، زیرا برای تفسیر مدل از ساختار درونی درخت استفاده می‌‌‌‌‌‌‌‌کند؛ به همین دلیل هم زمان اجرای آن بین دیتاست‌‌‌‌‌‌‌‌هایی با اندازه‌‌‌‌‌‌‌‌های متفاوت ثابت می‌‌‌‌‌‌‌‌ماند.

از سوی دیگر تفسیر الگوریتم‌‌‌‌‌‌‌‌های shap و جابجایی از داده‌‌‌‌‌‌‌‌های ورودی مستقل نیست و در نتیجه مقیاس‌‌‌‌‌‌‌‌پذیری آن‌‌‌‌‌‌‌‌ها به مشکل برمی‌‌‌‌‌‌‌‌خورد. با این حال مزیت روش جابجایی، استقلال خطی از تعداد مشاهدات و همچنین ستون‌‌‌‌‌‌‌‌هاست؛ روش‌‌‌‌‌‌‌‌های تشریح‌‌‌‌‌‌‌‌گر درخت Shap از تعداد مشاهدات و میزان پیچیدگی درخت (که به صورت O(TLD²) مشخص می‌شود) استقلال خطی دارند.

در نتیجه‌‌‌‌‌‌‌‌‌ی آن‌‌‌‌‌‌‌‌‌چه گفته شد به یک دوراهی برمی‌‌‌‌‌‌‌‌‌خوریم: با وجود برتری تقریبی Shap در دقت و پیچیدگی زمانی، این الگوریتم روی دیتاست‌‌‌‌‌‌‌‌‌های بزرگ از نظر زمانی به مشکل برخواهد خورد.

علاوه براین الگوریتم Boruta به خاطر محاسبه‌‌‌‌‌‌‌‌‌ی متوالی، قابلیت موازی‌‌‌‌‌‌‌‌‌سازی ندارد. پیشنهاد من برای کاهش زمان اجرایی، نمونه‌‌‌‌‌‌‌‌‌برداری از قسمتی از داده‌‌‌‌‌‌‌‌‌ها (در ازای مقداری واریانس برآورد Estimation variance) است.

من به جای انتخاب یک نمونه‌‌‌‌‌‌‌‌‌ی تصادفی در هر مرتبه تکرار، روشی خلق کردم که از طریق آن می‌‌‌‌‌‌‌‌‌توان کوچک‌‌‌‌‌‌‌‌‌ترین نمونه‌‌‌‌‌‌‌‌‌ی نماینده The smallest representative sample را در هر تکرار پیدا کرد.

بدین منظور داده‌‌‌‌‌‌‌‌‌ها را (با امتیازدهی به هر نمونه با Isolation Forest که مقداری بین -1 و +1 ارائه می‌‌‌‌‌‌‌‌‌دهد) به عنوان یک توزیع ناهنجار Anomaly distribution معرفی کردم. سپس کار را با نمونه‌‌‌‌‌‌‌‌‌ای با اندازه‌‌‌‌‌‌‌‌‌ی 5% داده‌‌‌‌‌‌‌‌‌های اصلی شروع کردم (احتمال انتخاب تصادفی این نمونه به این بستگی دارد که این نقطه‌‌‌‌‌‌‌‌‌ی داده‌‌‌‌‌‌‌‌‌ای خاص چطور از Isolation Forest استفاده می‌‌‌‌‌‌‌‌‌کند).

سپس با استفاده از آزمون‌‌‌‌‌‌‌‌‌های K این نمونه را با توزیع اصلی مقایسه کرده و تنها نمونه‌‌‌‌‌‌‌‌‌هایی که سطح اطمینان 95% و بالاتر داشتند را پذیرفتم. اگر هیچ نمونه‌‌‌‌‌‌‌‌‌ای با این سطح اطمینان وجود نداشته باشد، اندازه‌‌‌‌‌‌‌‌‌ی نمونه 5% افزایش یافته و این فرآیند دوباره تکرار می‌‌‌‌‌‌‌‌‌شود. این روش در آزمایش عملکرد بسیار خوبی داشت و زمان برخی از مسائل را تا 70% نیز کاهش داد.

اما این روش به واریانس مقادیر Shap می‌‌‌‌‌‌‌‌‌افزاید؛ با این حال رتبه‌‌‌‌‌‌‌‌‌بندی کلی و زیرمجموعه‌‌‌‌‌‌‌‌‌های ویژگی تولید شده‌‌‌‌‌‌‌‌‌ همچنان می‌‌‌‌‌‌‌‌‌توانند به خوبی نماینده‌‌‌‌‌‌‌‌‌ی کل دیتاست باشند.

توزیع تصادفی که در تصویر سمت چپ مشاهده می‌‌‌‌‌‌‌‌‌‌کنید، بازنمایی دقیقی از توزیع زیربنایی (که با آبی مشخص شده) نیست و به همین دلیل رد می‌‌‌‌‌‌‌‌‌‌شود. اما تصویر سمت راست، از آن‌‌‌‌‌‌‌‌‌‌جایی که دو توزیع مشخص شده با هم همخوانی دارند، پذیرفته می‌‌‌‌‌‌‌‌‌‌شود.

قبل از این‌‌‌‌‌‌‌‌‌‌که این رویکرد را به طور قطعی بپذیرم، یک تکنیک نمونه‌‌‌‌‌‌‌‌‌‌گیری دیگر (الهام‌‌‌‌‌‌‌‌‌‌گرفته از رویکرد نمونه‌‌‌‌‌‌‌‌‌‌گیری میانگین K که توسط تشریح‌‌‌‌‌‌‌‌‌‌گر کرنل Shap ارائه شده) را نیز اجرا کردم.

این رویکرد داده‌‌‌‌‌‌‌‌‌‌ها را خوشه‌‌‌‌‌‌‌‌‌‌بندی و از مراکز خوشه (که با الگوریتم میانگین K پیدا می‌‌‌‌‌‌‌‌‌‌شوند) به عنوان نقاط نمونه استفاده می‌‌‌‌‌‌‌‌‌‌کند. سپس به این نمونه‌‌‌‌‌‌‌‌‌‌ها بر اساس تعداد نقاط موجود در خوشه‌‌‌‌‌‌‌‌‌‌ای که نماینده‌‌‌‌‌‌‌‌‌‌ی آن هستند، وزن داده می‌‌‌‌‌‌‌‌‌‌شود.

این روش بدی نیست زیرا تعداد نمونه‌‌‌‌‌‌‌‌‌‌ها بسیار پایین بوده و در نتیجه سرعت را تا حد زیادی بهبود می‌‌‌‌‌‌‌‌‌‌بخشد. با این حال رتبه‌‌‌‌‌‌‌‌‌‌بندی کلی ویژگی و زیرمجموعه‌‌‌‌‌‌‌‌‌‌ها باقیمانده‌‌‌‌‌‌‌‌‌‌ی زیادی به جا می‌‌‌‌‌‌‌‌‌‌گذارند.

BorutaShap

بعد از همه‌‌‌‌‌‌‌‌‌‌‌ی این طرح‌‌‌‌‌‌‌‌‌‌‌ها و آزمایشات، تصمیم گرفتم این کد را بسته‌‌‌‌‌‌‌‌‌‌‌بندی کرده و در PYPI Artifactory در اختیار همگی قرار دهم. این بسته با استفاده از این دستور نصب pip به راحتی قابل استفاده است:

pip install BorutaShap

این بسته چندین ویژگی مثبت دارد که برای کاربران بالقوه مفید خواهد بود:

1. تنها اجرایی است که الگوریتم Boruta را با مقادیر Shapley ترکیب می‌‌‌‌‌‌‌‌‌‌‌کند.
2. قابلیت استفاده در مدل‌‌‌‌‌‌‌‌‌‌‌های درخت-محور را دارد (که می‌‌‌‌‌‌‌‌‌‌‌تواند در آینده به موارد دیگری هم گسترش یابد).
3. برخلاف سرعت پایین Shap، یک روش نمونه‌‌‌‌‌‌‌‌‌‌‌گیری منحصر به فرد برای افزایش سرعت در این روش به کار برده می‌‌‌‌‌‌‌‌‌‌‌شود. همچنین در صورت تمایل می‌‌‌‌‌‌‌‌‌‌‌توان از یک معیار اهمیت بهره برای افزایش سرعت استفاده کرد.
4. نتایج را می‌‌‌‌‌‌‌‌‌‌‌توان به راحتی مصورسازی کرد و اگر دیتاست بیش از حد بزرگ بود، می‌‌‌‌‌‌‌‌‌‌‌توان آن‌‌‌‌‌‌‌‌‌‌‌ها را به روی فرمت csv صادر کرد.

مثال

از نظر من رابط برنامه‌‌‌‌‌‌‌‌‌‌‌ی کاربردی قابلیت دسترسی خوبی دارد و متناسب با نیاز کاربران می‌‌‌‌‌‌‌‌‌‌‌باشد. برای نشان دادن این موضوع، یک فرآیند ساده از انتخاب ویژگی را روی دیتاست قیمت‌‌‌‌‌‌‌‌‌‌‌ خانه‌‌‌‌‌‌‌‌‌‌‌ی بوستون Boston House Pricing dataset توضیح خواهم داد.

این دیتاست یکی از دیتاست‌‌‌‌‌‌‌‌‌‌‌های عمده‌‌‌‌‌‌‌‌‌‌‌ی حوزه‌‌‌‌‌‌‌‌‌‌‌ی یادگیری ماشینی است و مسئله‌‌‌‌‌‌‌‌‌‌‌ی آن استفاده از 13 ویژگی (با مقادیر واقعی) برای پیش‌‌‌‌‌‌‌‌‌‌‌بینی میانه‌‌‌‌‌‌‌‌‌‌‌ی قیمت خانه است.

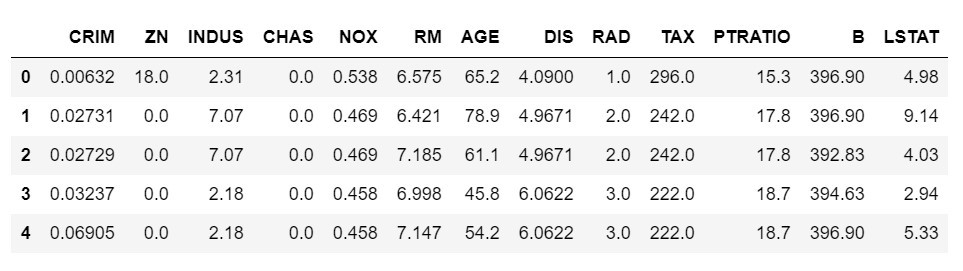
برای استفاده از ابزار انتخاب ویژگی BorutaShap می‌‌‌‌‌‌‌‌‌‌‌‌توانیم به سادگی با ایجاد یک نمونه کار را شروع کنیم. این شروع حداکثر به 5 پارامتر نیاز دارد: یک مدل درخت-محور طبق انتخاب خودتان (برای مثال یک درخت تصمیم‌‌‌‌‌‌‌‌‌‌‌‌ یا XGBoost که پیش‌‌‌‌‌‌‌‌‌‌‌‌فرض مدل جنگل تصادفی است)، معیار اهمیتی که می‌خواهید با آن میزان اهمیت ویژگی‌‌‌‌‌‌‌‌‌‌‌‌ها را بسنجید (مقادیر Shapley که پیش‌‌‌‌‌‌‌‌‌‌‌‌فرض است یا اهمیت Gini)، یک flag برای این‌‌‌‌‌‌‌‌‌‌‌‌که مشخص کنید مسئله مربوط به رده‌‌‌‌‌‌‌‌‌‌‌‌بندی است یا رگرسیون، یک پارامتر Percentile که درصد ویژگی سایه‌‌‌‌‌‌‌‌‌‌‌‌ی ماکزیمم را نشان داده و درنتیجه گزینش‌گر را آسان‌‌‌‌‌‌‌‌‌‌‌‌گیرتر می‌‌‌‌‌‌‌‌‌‌‌‌کند، و در نهایت یک مقدار- p یا سطح اطمینان که ویژگی بر اساس آن پذیرفته یا رد خواهد شد.

بعد ازاین‌‌‌‌‌‌‌‌‌‌‌‌که نمونه ساخته شد، نیاز داریم تابع تناسب Fit function را فرابخوانیم که خود 5 پارامتر دیگر دارد: X و y که واضح هستند، حالت تصادفی Random state برای ایجاد توانایی تولید مجدد  اضافه می‌‌‌‌‌‌‌‌‌‌‌‌شود، n_trials که به تعداد دفعات آزمایش یا تکرارهای الگوریتم مدنظر شما اشاره دارد، و یک پارامتر بولین نمونه A Boolean sample parameter ‌‌‌‌‌‌‌‌‌‌‌‌ که اگر درست  باشد، از تکنیک نمونه‌‌‌‌‌‌‌‌‌‌‌‌گیری که بالا توضیح داده شد برای سرعت بخشیدن به فرآیند استفاده می‌کند.

همانطور که مشاهده می‌‌‌‌‌‌‌‌‌‌‌‌‌کنید، الگوریتم 9 تا از 13 ویژگی را به عنوان پیش‌‌‌‌‌‌‌‌‌‌‌‌‌بین‌‌‌‌‌‌‌‌‌‌‌‌‌های مهم متغیرهای هدف تأیید کرد. در حالی‌‌‌‌‌‌‌‌‌‌‌‌‌که چهار ویژگی دیگر به خاطر عملکرد پیوسته ضعیفشان (نسبت به متغیرهای تصادفی دیگر) رد شدند.

در این مثال هیچ کدام از ویژگی‌‌‌‌‌‌‌‌‌‌‌‌‌ها غیرقطعی tentative نبودند؛ ویژگی غیرقطعی زمانی تولید می‌‌‌‌‌‌‌‌‌‌‌‌‌شود که الگوریتم از رد یا پذیرش یک ویژگی مطمئن نیست. وقتی با چنین مسئله‌‌‌‌‌‌‌‌‌‌‌‌‌ای روبرو می‌‌‌‌‌‌‌‌‌‌‌‌‌شوید سه راه‌‌‌‌‌‌‌‌‌‌‌‌‌ خواهید داشت: می‌‌‌‌‌‌‌‌‌‌‌‌‌توانید الگوریتم را با تکرارهای بیشتر اجرا کنید، خود به نمودار نگاه کرده و تصمیم بگیرید آیا این ویژگی مهم است یا خیر، و یا این‌‌‌‌‌‌‌‌‌‌‌‌‌که از تابع TenativeRoughFix() استفاده کنید (این تابع میزان میانه‌‌‌‌‌‌‌‌‌‌‌‌‌ی اهمیت ویژگی‌‌‌‌‌‌‌‌‌‌‌‌‌های غیرقطعی را با میزان میانه‌‌‌‌‌‌‌‌‌‌‌‌‌ی اهمیت برگرفته از ماکزیموم متغیر تصادفی مقایسه می‌‌‌‌‌‌‌‌‌‌‌‌‌کند تا تصمیم بگیرد ویژگی را بپذیرد یا رد کند).

برای مصورسازی نتایج می‌‌‌‌‌‌‌‌‌‌‌‌‌توانید به آسانی از تابع نمودار استفاده کنید که چندین پارامتر دارد: لگاریتم محور y که به صورت پیش‌‌‌‌‌‌‌‌‌‌‌‌‌فرض انتخاب می‌‌‌‌‌‌‌‌‌‌‌‌‌شود زیرا منجر به مصورسازی بهتر می‌‌‌‌‌‌‌‌‌‌‌‌‌گردد (بدون این پارامتر، جعبه‌‌‌‌‌‌‌‌‌‌‌‌‌ها به دلیل مقیاس‌‌‌‌‌‌‌‌‌‌‌‌‌های متفاوتی که دارند به سختی دیده می‌‌‌‌‌‌‌‌‌‌‌‌‌شوند)، پارامتر which_features که چهار حالت مختلف دارد: “همه”، “پذیرفته ‌‌‌‌‌‌‌‌‌‌‌‌‌شده”، “رد شده”، و “غیرقطعی”. اگر نمودار بیش از حد شلوغ شد، تابعی وجود دارد که با استفاده از آن می‌‌‌‌‌‌‌‌‌‌‌‌‌توانید نتایج خود را به فرمت csv ذخیره کنید تا فهم آسان‌‌‌‌‌‌‌‌‌‌‌‌‌تری داشته باشند.

سپس به راحتی می‌­توانیم تابع زیرمجموعه را فرابخوانیم تا زیرمجموعه بهینه‌­ای از ویژگی‌­ها را از چارچوب داده­‌های اصلی بگیریم و آن را ذخیره یا برای مقاصد مدل­‌سازی استفاده کنیم.

در این کدنوشته به شما نشان داده می‌‌‌‌‌‌‌‌‌‌‌‌‌‌شود چطور از BorutaShap برای مدل‌‌‌‌‌‌‌‌‌‌‌‌‌‌های درخت-محور گوناگون استفاده کنید. من نتایج به دست آمده را جالب دانستم، زیرا هر مدل زیرمجموعه‌‌‌‌‌‌‌‌‌‌‌‌‌‌ی بهینه‌‌‌‌‌‌‌‌‌‌‌‌‌‌ی خاص خود را از داده‌‌‌‌‌‌‌‌‌‌‌‌‌‌ها ارائه می‌‌‌‌‌‌‌‌‌‌‌‌‌‌دهد؛ امری که خود نشان‌‌‌‌‌‌‌‌‌‌‌‌‌‌گر اهمیت استفاده از مدل منتخب خود برای فرآیند انتخاب ویژگی است.

نتیجه‌‌‌‌‌‌‌‌‌‌‌‌‌‌گیری

BorutaShap در مقایسه با روش‌‌‌‌‌‌‌‌‌‌‌‌‌‌های بهره و جابجایی دقیق‌‌‌‌‌‌‌‌‌‌‌‌‌‌ترین زیرمجموعه از ویژگی‌‌‌‌‌‌‌‌‌‌‌‌‌‌ها را ارائه می‌دهد. با این‌‌‌‌‌‌‌‌‌‌‌‌‌‌که می‌‌‌‌‌‌‌‌‌‌‌‌‌‌دانم هرچیزی نقطه‌‌‌‌‌‌‌‌‌‌‌‌‌‌ضعفی هم دارد، می‌‌‌‌‌‌‌‌‌‌‌‌‌‌توانم بگویم الگوریتم BorutaShap انتخاب خوبی برای هر مسئله‌‌‌‌‌‌‌‌‌‌‌‌‌‌ی انتخاب ویژگی خودکار Automatic feature selection است.

این الگوریتم نه تنها بهترین زیرمجموعه از ویژگی‌‌‌‌‌‌‌‌‌‌‌‌‌‌ها را فراهم می‌‌‌‌‌‌‌‌‌‌‌‌‌‌کند، بلکه از نظر تئوری، model agnostic هم بوده و شما را قادر می‌‌‌‌‌‌‌‌‌‌‌‌‌‌سازد مدل جنگل تصادفی را با مدل مدنظر خود جایگزین کنید. علاوه بر این، مقادیر Shapely دقیق‌‌‌‌‌‌‌‌‌‌‌‌‌‌ترین و پایاترین نتایج را از رتبه‌‌‌‌‌‌‌‌‌‌‌‌‌‌بندی کلی ارائه می‌‌‌‌‌‌‌‌‌‌‌‌‌‌دهد؛ این مزیت علاوه بر ارائه‌‌‌‌‌‌‌‌‌‌‌‌‌‌ی واریانس برای هر تکرار ابزار استنتاجی بسیار خوبی به دست می‌‌‌‌‌‌‌‌‌‌‌‌‌‌دهد که به کاربر بینشی درست از کارکرد داخلی مدل جعبه‌‌‌‌‌‌‌‌‌‌‌‌‌‌سیاهشان Inner workings of their black box model خواهد بخشید.